Open book
|
The users responsible for this page are: Jack Calcut, Horst Winkelnkemper. No other users may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Open Books
The simplest general definition of an open book, as the concept first appeared explicitly in the literature [Winkelnkemper1973], is the following.
Let  be a smooth, compact
be a smooth, compact  -manifold with
-manifold with 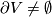 . Let
. Let 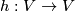 be a diffeomorphism that restricts to the identity on
be a diffeomorphism that restricts to the identity on 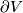 . The mapping torus of
. The mapping torus of  , denoted
, denoted 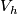 , has
, has 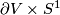 as boundary. By identifying
as boundary. By identifying 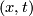 with
with 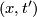 for each
for each 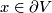 and
and 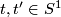 , we obtain a smooth, closed
, we obtain a smooth, closed  -manifold
-manifold  . Let
. Let  denote the image of
denote the image of 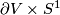 under the identification map.
under the identification map.
Definition 1.1. A closed manifold is an open book provided it is diffeomorphic to  . The fibers
. The fibers 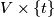 of
of 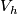 , where
, where 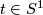 , are codimension
, are codimension  submanifolds of
submanifolds of  whose images are the pages of the open book. The image of the closed, codimension 2 submanifold
whose images are the pages of the open book. The image of the closed, codimension 2 submanifold  of
of  is called the binding of the open book.
is called the binding of the open book.
For an open book  , every point
, every point 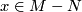 lies on one and only one page, and
lies on one and only one page, and  is the boundary
of each page.
is the boundary
of each page.
Sometimes for certain homological and/or analytic applications (for example, [Barreto&Medrano&Verjovsky2013, p. 3], [Quinn1979, p. 55], and [Ranicki1998, p. 252]) one uses more elaborate, but equivalent, definitions. Furthermore, one can generalize the open book definition to compact manifolds with nonempty boundaries [Ranicki1998, p. 353], [Quinn1979, p. 55]. For nice figures, see [Giroux2005], [Ranicki1998, p. 616], and [Winkelnkemper1973].
The first general open book existence theorem was obtained in 1972:
Theorem 1.2 [Winkelnkemper1973] .
If 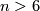 and
and 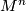 is simply connected, then
is simply connected, then 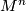 is an open book if and only if its signature is
is an open book if and only if its signature is  .
.
In general, if 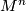 is orientable and
is orientable and 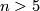 , then the existence of open book structures was settled by T. Lawson when
, then the existence of open book structures was settled by T. Lawson when  is odd: there is no obstruction, and for any
is odd: there is no obstruction, and for any 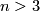 by F. Quinn: when
by F. Quinn: when  is even, the obstruction lies in the asymmetric Witt group of
is even, the obstruction lies in the asymmetric Witt group of ![\mathbb{Z}[\pi_{1}(M^n)]](/images/math/3/c/f/3cf25241a62436c1fe5c74ed4f17bf3d.png) , generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if
, generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if  , then every closed, orientable
, then every closed, orientable 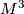 is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such
is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such 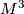 contains a fibered knot) or be as simple as possible: a compact
contains a fibered knot) or be as simple as possible: a compact  -disk with holes.
-disk with holes.
2 Applications
Open book decompositions have had numerous applications (see the Appendix in [Ranicki1998]). More recent applications are to: diffusion processes and the averaging principle [Freidlin&Wentzell2004], contact forms on moment angle manifolds [Barreto&Medrano&Verjovsky2013], and Haefliger's singular foliations [Laudenbach&Meigniez2012]. Most notably, in dimension  , open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable
, open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable  -manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable
-manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable  -manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
-manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
Another notable feature was discovered by González-Acuña: in dimension  and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the
and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the  -manifold. Thus, the whole theory of closed, orientable
-manifold. Thus, the whole theory of closed, orientable  -manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
-manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
3 References
- [Barreto&Medrano&Verjovsky2013] Y. Barreto, S. López de Medrano and A. Verjovsky, Open Book Structures on Moment-Angle Manifolds
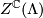 and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
- [Calcut2005] J. S. Calcut, Knot theory and the Casson invariant in the Artin presentation theory, Fundamental and Applied Mathematics 11 No. 4, L. V. Keldysh Memorial Proceedings, Moscow, (2005), 119--126. MR2192960 (2006m:57013)
- [Etnyre2006] J. B. Etnyre, Lectures on open book decompositions and contact structures, in Floer homology, gauge theory, and low-dimensional topology, 103–141, Clay Math. Proc., 5, Amer. Math. Soc., (2006). MR2249250 (2007g:57042) Zbl 1108.53050
- [Freidlin&Wentzell2004] M. I. Freidlin and A. D. Wentzell, Diffusion processes on an open book and the averaging principle, Stochastic Process. Appl. 113 (2004), no.1, 101–126. MR2078539 (2005e:60178) Zbl 1075.60100
- [Giroux2005] E. Giroux, What is...an Open Book?, Notices of the Amer. Math. Soc. 52 (2005), 42–43.
- [Laudenbach&Meigniez2012] F. Laudenbach and G. Meigniez, Haefliger's codimension-one singular foliations, open books and twisted open books in dimension 3, Bull. Braz. Math. Soc. (N.S.) 43 (2012), 347–373. MR3024060 Zbl 1263.57022
- [Quinn1979] F. Quinn, Open book decompositions, and the bordism of automorphisms, Topology 18 (1979), no.1, 55–73. MR528236 (81e:57027) Zbl 0425.57010
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Thurston&Winkelnkemper1975] W. P. Thurston and H. E. Winkelnkemper, On the existence of contact forms, Proc. Amer. Math. Soc. 52 (1975), 345–347. MR0375366 (51 #11561) Zbl 0312.53028
- [Winkelnkemper1973] H. E. Winkelnkemper, Manifolds as open books, Bull. Amer. Math. Soc. 79 (1973), 45–51. MR0310912 (46 #10010) Zbl 0269.57011
- [Winkelnkemper2002] H. E. Winkelnkemper, Artin presentations. I. Gauge theory,
 TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026
TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026
 -manifold with
-manifold with 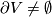 . Let
. Let 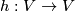 be a diffeomorphism that restricts to the identity on
be a diffeomorphism that restricts to the identity on 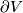 . The mapping torus of
. The mapping torus of  , denoted
, denoted 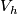 , has
, has 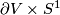 as boundary. By identifying
as boundary. By identifying 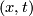 with
with 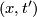 for each
for each 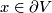 and
and 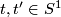 , we obtain a smooth, closed
, we obtain a smooth, closed  -manifold
-manifold  . Let
. Let  denote the image of
denote the image of 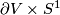 under the identification map.
under the identification map.
Definition 1.1. A closed manifold is an open book provided it is diffeomorphic to  . The fibers
. The fibers 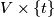 of
of 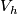 , where
, where 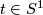 , are codimension
, are codimension  submanifolds of
submanifolds of  whose images are the pages of the open book. The image of the closed, codimension 2 submanifold
whose images are the pages of the open book. The image of the closed, codimension 2 submanifold  of
of  is called the binding of the open book.
is called the binding of the open book.
For an open book  , every point
, every point 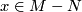 lies on one and only one page, and
lies on one and only one page, and  is the boundary
of each page.
is the boundary
of each page.
Sometimes for certain homological and/or analytic applications (for example, [Barreto&Medrano&Verjovsky2013, p. 3], [Quinn1979, p. 55], and [Ranicki1998, p. 252]) one uses more elaborate, but equivalent, definitions. Furthermore, one can generalize the open book definition to compact manifolds with nonempty boundaries [Ranicki1998, p. 353], [Quinn1979, p. 55]. For nice figures, see [Giroux2005], [Ranicki1998, p. 616], and [Winkelnkemper1973].
The first general open book existence theorem was obtained in 1972:
Theorem 1.2 [Winkelnkemper1973] .
If 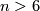 and
and 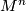 is simply connected, then
is simply connected, then 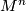 is an open book if and only if its signature is
is an open book if and only if its signature is  .
.
In general, if 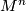 is orientable and
is orientable and 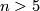 , then the existence of open book structures was settled by T. Lawson when
, then the existence of open book structures was settled by T. Lawson when  is odd: there is no obstruction, and for any
is odd: there is no obstruction, and for any 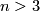 by F. Quinn: when
by F. Quinn: when  is even, the obstruction lies in the asymmetric Witt group of
is even, the obstruction lies in the asymmetric Witt group of ![\mathbb{Z}[\pi_{1}(M^n)]](/images/math/3/c/f/3cf25241a62436c1fe5c74ed4f17bf3d.png) , generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if
, generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if  , then every closed, orientable
, then every closed, orientable 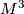 is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such
is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such 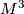 contains a fibered knot) or be as simple as possible: a compact
contains a fibered knot) or be as simple as possible: a compact  -disk with holes.
-disk with holes.
2 Applications
Open book decompositions have had numerous applications (see the Appendix in [Ranicki1998]). More recent applications are to: diffusion processes and the averaging principle [Freidlin&Wentzell2004], contact forms on moment angle manifolds [Barreto&Medrano&Verjovsky2013], and Haefliger's singular foliations [Laudenbach&Meigniez2012]. Most notably, in dimension  , open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable
, open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable  -manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable
-manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable  -manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
-manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
Another notable feature was discovered by González-Acuña: in dimension  and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the
and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the  -manifold. Thus, the whole theory of closed, orientable
-manifold. Thus, the whole theory of closed, orientable  -manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
-manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
3 References
- [Barreto&Medrano&Verjovsky2013] Y. Barreto, S. López de Medrano and A. Verjovsky, Open Book Structures on Moment-Angle Manifolds
 and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
- [Calcut2005] J. S. Calcut, Knot theory and the Casson invariant in the Artin presentation theory, Fundamental and Applied Mathematics 11 No. 4, L. V. Keldysh Memorial Proceedings, Moscow, (2005), 119--126. MR2192960 (2006m:57013)
- [Etnyre2006] J. B. Etnyre, Lectures on open book decompositions and contact structures, in Floer homology, gauge theory, and low-dimensional topology, 103–141, Clay Math. Proc., 5, Amer. Math. Soc., (2006). MR2249250 (2007g:57042) Zbl 1108.53050
- [Freidlin&Wentzell2004] M. I. Freidlin and A. D. Wentzell, Diffusion processes on an open book and the averaging principle, Stochastic Process. Appl. 113 (2004), no.1, 101–126. MR2078539 (2005e:60178) Zbl 1075.60100
- [Giroux2005] E. Giroux, What is...an Open Book?, Notices of the Amer. Math. Soc. 52 (2005), 42–43.
- [Laudenbach&Meigniez2012] F. Laudenbach and G. Meigniez, Haefliger's codimension-one singular foliations, open books and twisted open books in dimension 3, Bull. Braz. Math. Soc. (N.S.) 43 (2012), 347–373. MR3024060 Zbl 1263.57022
- [Quinn1979] F. Quinn, Open book decompositions, and the bordism of automorphisms, Topology 18 (1979), no.1, 55–73. MR528236 (81e:57027) Zbl 0425.57010
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Thurston&Winkelnkemper1975] W. P. Thurston and H. E. Winkelnkemper, On the existence of contact forms, Proc. Amer. Math. Soc. 52 (1975), 345–347. MR0375366 (51 #11561) Zbl 0312.53028
- [Winkelnkemper1973] H. E. Winkelnkemper, Manifolds as open books, Bull. Amer. Math. Soc. 79 (1973), 45–51. MR0310912 (46 #10010) Zbl 0269.57011
- [Winkelnkemper2002] H. E. Winkelnkemper, Artin presentations. I. Gauge theory,
 TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026
TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026
 -manifold with
-manifold with 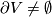 . Let
. Let 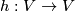 be a diffeomorphism that restricts to the identity on
be a diffeomorphism that restricts to the identity on 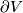 . The mapping torus of
. The mapping torus of  , denoted
, denoted 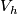 , has
, has 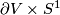 as boundary. By identifying
as boundary. By identifying 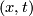 with
with 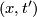 for each
for each 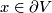 and
and 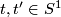 , we obtain a smooth, closed
, we obtain a smooth, closed  -manifold
-manifold  . Let
. Let  denote the image of
denote the image of 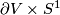 under the identification map.
under the identification map.
Definition 1.1. A closed manifold is an open book provided it is diffeomorphic to  . The fibers
. The fibers 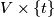 of
of 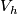 , where
, where 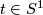 , are codimension
, are codimension  submanifolds of
submanifolds of  whose images are the pages of the open book. The image of the closed, codimension 2 submanifold
whose images are the pages of the open book. The image of the closed, codimension 2 submanifold  of
of  is called the binding of the open book.
is called the binding of the open book.
For an open book  , every point
, every point 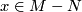 lies on one and only one page, and
lies on one and only one page, and  is the boundary
of each page.
is the boundary
of each page.
Sometimes for certain homological and/or analytic applications (for example, [Barreto&Medrano&Verjovsky2013, p. 3], [Quinn1979, p. 55], and [Ranicki1998, p. 252]) one uses more elaborate, but equivalent, definitions. Furthermore, one can generalize the open book definition to compact manifolds with nonempty boundaries [Ranicki1998, p. 353], [Quinn1979, p. 55]. For nice figures, see [Giroux2005], [Ranicki1998, p. 616], and [Winkelnkemper1973].
The first general open book existence theorem was obtained in 1972:
Theorem 1.2 [Winkelnkemper1973] .
If 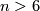 and
and 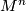 is simply connected, then
is simply connected, then 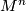 is an open book if and only if its signature is
is an open book if and only if its signature is  .
.
In general, if 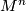 is orientable and
is orientable and 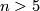 , then the existence of open book structures was settled by T. Lawson when
, then the existence of open book structures was settled by T. Lawson when  is odd: there is no obstruction, and for any
is odd: there is no obstruction, and for any 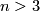 by F. Quinn: when
by F. Quinn: when  is even, the obstruction lies in the asymmetric Witt group of
is even, the obstruction lies in the asymmetric Witt group of ![\mathbb{Z}[\pi_{1}(M^n)]](/images/math/3/c/f/3cf25241a62436c1fe5c74ed4f17bf3d.png) , generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if
, generalizing the Wall surgery obstruction [Ranicki1998, p. 360]. In 1975, González-Acuña used fundamental work of Alexander and Lickorish to prove: if  , then every closed, orientable
, then every closed, orientable 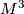 is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such
is an open book; furthermore, the page can be chosen to have a connected boundary (that is, every such 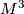 contains a fibered knot) or be as simple as possible: a compact
contains a fibered knot) or be as simple as possible: a compact  -disk with holes.
-disk with holes.
2 Applications
Open book decompositions have had numerous applications (see the Appendix in [Ranicki1998]). More recent applications are to: diffusion processes and the averaging principle [Freidlin&Wentzell2004], contact forms on moment angle manifolds [Barreto&Medrano&Verjovsky2013], and Haefliger's singular foliations [Laudenbach&Meigniez2012]. Most notably, in dimension  , open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable
, open books are crucial for proving Giroux's theorem that, roughly put, on any closed, orientable  -manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable
-manifold there is a one-to-one correspondence between contact forms (Geometry) and open books (Topology) [Etnyre2006]. In other words, every contact form on a closed, orientable  -manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
-manifold arises via an open book as in the construction of contact forms by Thurston and Winkelnkemper [Thurston&Winkelnkemper1975].
Another notable feature was discovered by González-Acuña: in dimension  and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the
and when the page is planar, the monodromy homeomorphism of the page can be substituted by a purely discrete presentation, an Artin presentation of the fundamental group of the  -manifold. Thus, the whole theory of closed, orientable
-manifold. Thus, the whole theory of closed, orientable  -manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
-manifolds is encoded in the purely discrete, group-theoretic theory of Artin presentations [Winkelnkemper2002], [Ranicki1998, p. 617]. This theory is now an autonomous one with purely group-theoretic analogues of the Casson invariant [Calcut2005] and Donaldson's Theorem [Ranicki1998, p. 621], [Winkelnkemper2002, p. 240].
3 References
- [Barreto&Medrano&Verjovsky2013] Y. Barreto, S. López de Medrano and A. Verjovsky, Open Book Structures on Moment-Angle Manifolds
 and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
and Higher Dimensional Contact Manifolds, (2013). Available at the arXiv:1303.2671.
- [Calcut2005] J. S. Calcut, Knot theory and the Casson invariant in the Artin presentation theory, Fundamental and Applied Mathematics 11 No. 4, L. V. Keldysh Memorial Proceedings, Moscow, (2005), 119--126. MR2192960 (2006m:57013)
- [Etnyre2006] J. B. Etnyre, Lectures on open book decompositions and contact structures, in Floer homology, gauge theory, and low-dimensional topology, 103–141, Clay Math. Proc., 5, Amer. Math. Soc., (2006). MR2249250 (2007g:57042) Zbl 1108.53050
- [Freidlin&Wentzell2004] M. I. Freidlin and A. D. Wentzell, Diffusion processes on an open book and the averaging principle, Stochastic Process. Appl. 113 (2004), no.1, 101–126. MR2078539 (2005e:60178) Zbl 1075.60100
- [Giroux2005] E. Giroux, What is...an Open Book?, Notices of the Amer. Math. Soc. 52 (2005), 42–43.
- [Laudenbach&Meigniez2012] F. Laudenbach and G. Meigniez, Haefliger's codimension-one singular foliations, open books and twisted open books in dimension 3, Bull. Braz. Math. Soc. (N.S.) 43 (2012), 347–373. MR3024060 Zbl 1263.57022
- [Quinn1979] F. Quinn, Open book decompositions, and the bordism of automorphisms, Topology 18 (1979), no.1, 55–73. MR528236 (81e:57027) Zbl 0425.57010
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Thurston&Winkelnkemper1975] W. P. Thurston and H. E. Winkelnkemper, On the existence of contact forms, Proc. Amer. Math. Soc. 52 (1975), 345–347. MR0375366 (51 #11561) Zbl 0312.53028
- [Winkelnkemper1973] H. E. Winkelnkemper, Manifolds as open books, Bull. Amer. Math. Soc. 79 (1973), 45–51. MR0310912 (46 #10010) Zbl 0269.57011
- [Winkelnkemper2002] H. E. Winkelnkemper, Artin presentations. I. Gauge theory,
 TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026
TQFT's and the braid groups, J. Knot Theory Ramifications 11 (2002), no.2, 223–275. MR1895372 (2003b:57045) Zbl 0994.57026