Novikov additivity I (Ex)
(Difference between revisions)
Tibor Macko (Talk | contribs) (Created page with "<wikitex>; Let $(Y,X)$ be a $2n$-dimensional manifold with boundary, $n = 2k$. Consider the homomorphism $\varphi \colon H^{n} (Y,X) \rightarrow H^{n} (X)$ and denote $\wideha...") |
Tibor Macko (Talk | contribs) |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Let $(Y,X)$ be a $2n$-dimensional manifold with boundary, $n = 2k$. Consider the homomorphism $\varphi \colon H^{n} (Y,X) \rightarrow H^{n} (X)$ and denote $\ | + | Let $(Y,X)$ be a $2n$-dimensional manifold with boundary, $n = 2k$. Consider the homomorphism $\varphi \colon H^{n} (Y,X) \rightarrow H^{n} (X)$ and denote $\hat{H}^{n} (Y)$ the image of $\varphi$. Coefficients are understood to be in $\mathbb{R}$. |
The middle dimensional intersection form | The middle dimensional intersection form | ||
| Line 6: | Line 6: | ||
H^{n} (Y) \otimes H^{n} (Y) \rightarrow \mathbb{R} | H^{n} (Y) \otimes H^{n} (Y) \rightarrow \mathbb{R} | ||
$$ | $$ | ||
| − | is degenerate in general. Show that the intersection form $B$ on $\ | + | is degenerate in general. Show that the intersection form $B$ on $\hat{H}^{n} (Y)$ defined by |
$$ | $$ | ||
B(\varphi (a), \varphi (b)) = \langle a \cup b , [Y] \rangle | B(\varphi (a), \varphi (b)) = \langle a \cup b , [Y] \rangle | ||
Revision as of 10:05, 29 May 2012
Let 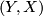 be a
be a  -dimensional manifold with boundary,
-dimensional manifold with boundary, 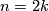 . Consider the homomorphism
. Consider the homomorphism 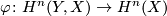 and denote
and denote 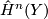 the image of
the image of  . Coefficients are understood to be in
. Coefficients are understood to be in 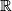 .
.
The middle dimensional intersection form
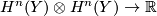
is degenerate in general. Show that the intersection form  on
on 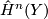 defined by
defined by
![\displaystyle B(\varphi (a), \varphi (b)) = \langle a \cup b , [Y] \rangle](/images/math/7/8/3/7837ea77f99e8d1f0cafe5f705940a2a.png)
is a non-degenerate symmetric bilinear form and let us define the signature 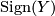 to be the signature of this form.
to be the signature of this form.
Suppose that we have also another  -dimensional manifold
-dimensional manifold 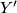 with boundary
with boundary 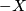 . Form the closed manifold
. Form the closed manifold 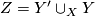 . Show that
. Show that
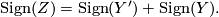
Hint: section 7 of ASIT III