Normal invariants and G/O (Ex)
From Manifold Atlas
Revision as of 18:29, 2 April 2012 by Andreas Hermann (Talk | contribs)
The aim of these exercises is to follow the proof of [Lück2001, Theorem 3.45].
Given the map 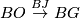 , define
, define 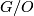 to be the homotopy fibre of
to be the homotopy fibre of 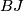 :
:
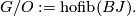
In [Lück2001, p. 66] there is defined a group of stable fibre homotopy trivialisations of smooth vector bundles over a space  which is denoted
which is denoted 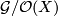 .
.
Exercise 0.1.
Show that for any space  there is a bijection
there is a bijection
![\displaystyle [X, G/O] \equiv \mathcal{G}/\mathcal{O}(X).](/images/math/a/7/9/a798bfe513cc78686eba1e09d8e2a7c1.png)