Normal invariants and G/O (Ex)
(Difference between revisions)
m |
m |
||
| Line 3: | Line 3: | ||
Given the map $BO\stackrel{BJ}\to{BG}$, define $G/O$ to be the homotopy fibre of $BJ$: | Given the map $BO\stackrel{BJ}\to{BG}$, define $G/O$ to be the homotopy fibre of $BJ$: | ||
| − | $$G/O:=\text{hofib}(J)$$ | + | $$G/O:=\text{hofib}(J).$$ |
In {{citeD|Lück2001|p 61}} there is defined a group of stable fibre homotopy trivialisations of smooth vector bundles over a space $X$ which is denoted $\mathcal{G}/\mathcal{O}(X)$. | In {{citeD|Lück2001|p 61}} there is defined a group of stable fibre homotopy trivialisations of smooth vector bundles over a space $X$ which is denoted $\mathcal{G}/\mathcal{O}(X)$. | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
Revision as of 10:42, 27 March 2012
The aim of these exercises is to follow the proof of [Lück2001, Theorem 3.45].
Given the map 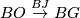 , define
, define 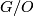 to be the homotopy fibre of
to be the homotopy fibre of 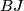 :
:
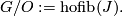
In [Lück2001, p 61] there is defined a group of stable fibre homotopy trivialisations of smooth vector bundles over a space  which is denoted
which is denoted 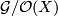 .
.
Exercise 0.1.
Show that for any space  there is a bijection
there is a bijection
![\displaystyle [X, G/O] \equiv \mathcal{G}/\mathcal{O}(X).](/images/math/a/7/9/a798bfe513cc78686eba1e09d8e2a7c1.png)