Microbundle
m |
Marek Kaluba (Talk | contribs) (Definition of isomorphism) |
||
| Line 6: | Line 6: | ||
An $n$-dimensional microbundle is a quadruple $(E,B,i,j)$ such that there is a sequence $$B\xrightarrow{i} E\xrightarrow{j} B$$ and the following conditions hold. | An $n$-dimensional microbundle is a quadruple $(E,B,i,j)$ such that there is a sequence $$B\xrightarrow{i} E\xrightarrow{j} B$$ and the following conditions hold. | ||
#$j\circ i=\id_B$ | #$j\circ i=\id_B$ | ||
| − | #for all $x\in B$ there exist open neigbourhood $U\subset B$ | + | #for all $x\in B$ there exist open neigbourhood $U\subset B$, an open neighbourhood $V\subset E$ of $i(b)$ and a homeomorphism $$h \colon V \to U\times \mathbb{R}^n$$ |
| − | + | which makes the following diagram commute: | |
| − | + | ||
$$ \xymatrix{& V \ar[dr]^{j|_V} \ar[dd] \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}} $$ | $$ \xymatrix{& V \ar[dr]^{j|_V} \ar[dd] \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}} $$ | ||
{{endthm}} | {{endthm}} | ||
| Line 21: | Line 20: | ||
{{endrem}} | {{endrem}} | ||
| − | + | {{beginthm|Definition}} | |
| + | Two microbundles $(E_n,X,i_n,j_n)$, $n=1,2$ over the same space $X$ are isomorphic if there exist neighbourhoods $V_1\subset E_1$ of $i_1(B)$ and $V_2\subset E_2$ of $i_2(B)$ and a homeomorphism $H\colon V_1\to V_2$ making the following diagram commute. | ||
| + | |||
| + | $$ | ||
| + | \xymatrix{ | ||
| + | & V_1 \ar[dd]^H\ar[rd]^{j_1|_{V_1}} \\ | ||
| + | B\ar[ru]^{i_1}\ar[rd]_{i_2} & & B \\ | ||
| + | & V_2 \ar[ru]_{j_2|_{V_2}} | ||
| + | } | ||
| + | $$ | ||
| + | |||
| + | {{endthm|Definition}} | ||
{{beginthm|Theorem|\cite{Kister1964|Theorem 2} }} | {{beginthm|Theorem|\cite{Kister1964|Theorem 2} }} | ||
Revision as of 22:37, 29 May 2012
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:20, 16 May 2013 and the changes since publication. |
1 Introduction
The concept of Microbundle of dimension  was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later [Kister1964] showed that every microbundle uniquely determines a topological
was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later [Kister1964] showed that every microbundle uniquely determines a topological  -bundle.
-bundle.
Definition 1.1 [Milnor1964] .
An -dimensional microbundle is a quadruple
-dimensional microbundle is a quadruple 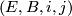 such that there is a sequence
such that there is a sequence 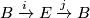
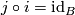
- for all
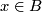 there exist open neigbourhood
there exist open neigbourhood  , an open neighbourhood
, an open neighbourhood  of
of 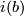 and a homeomorphism
and a homeomorphism 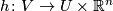
which makes the following diagram commute:
![\displaystyle \xymatrix{& V \ar[dr]^{j|_V} \ar[dd] \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}}](/images/math/a/1/4/a1489c27410f30906c655cf1043aba2d.png)
Example 1.2 [Milnor1964, Lemma 2.1].
Let  be topological
be topological  -manifold, let
-manifold, let  be the diagonal map and let
be the diagonal map and let 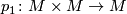 be the projection onto the first factor. Then
be the projection onto the first factor. Then
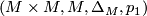
is an  -dimensional microbundle.
-dimensional microbundle.
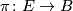 be a topological
be a topological  -bundle with zero section
-bundle with zero section 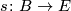 . Then
. Then 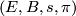
is an  -dimensional microbundle.
-dimensional microbundle.
Definition 1.4.
Two microbundles 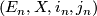 ,
, 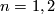 over the same space
over the same space  are isomorphic if there exist neighbourhoods
are isomorphic if there exist neighbourhoods 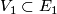 of
of 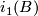 and
and 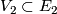 of
of 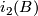 and a homeomorphism
and a homeomorphism 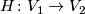 making the following diagram commute.
making the following diagram commute.
![\displaystyle \xymatrix{ & V_1 \ar[dd]^H\ar[rd]^{j_1|_{V_1}} \\ B\ar[ru]^{i_1}\ar[rd]_{i_2} & & B \\ & V_2 \ar[ru]_{j_2|_{V_2}} }](/images/math/3/e/e/3eeea919d105147cb118a6c2e83d8793.png)
Theorem 1.5 [Kister1964, Theorem 2] .
Let 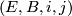 be an
be an  -dimensional microbundle. Then there is a neighbourhood of
-dimensional microbundle. Then there is a neighbourhood of 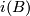 ,
, 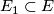 such that:
such that:
-
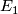 is the total space of a topological
is the total space of a topological  -bundle over
-bundle over  .
.
- The inclusion
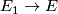 is a microbundle isomorphism
is a microbundle isomorphism
- If
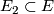 is any other such neighbourhood of
is any other such neighbourhood of 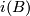 then there is a
then there is a  -bundle isomorphism
-bundle isomorphism 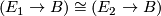 .
.
2 References
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404