Microbundle
Latest revision as of 14:20, 16 May 2013
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:20, 16 May 2013 and the changes since publication. |
|
The users responsible for this page are: Diarmuid Crowley, Matthias Kreck. No other users may edit this page at present. |
Contents |
1 Definition
The concept of a microbundle of dimension  was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later Kister [Kister1964], and independently Mazur, showed that every microbundle uniquely determines a topological
was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later Kister [Kister1964], and independently Mazur, showed that every microbundle uniquely determines a topological  -bundle; i.e. a fibre bundle with structure group the homeomorphisms of
-bundle; i.e. a fibre bundle with structure group the homeomorphisms of  fixing
fixing  .
.
Definition 1.1 [Milnor1964] .
Let  be a topological space. An
be a topological space. An  -dimensional microbundle over
-dimensional microbundle over  is a quadruple
is a quadruple 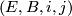 where
where  is a space,
is a space,  and
and  are maps fitting into the following diagram
are maps fitting into the following diagram
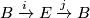
and the following conditions hold:
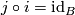 .
.
- For all
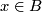 there exist open neigbourhood
there exist open neigbourhood  , an open neighbourhood
, an open neighbourhood  of
of 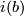 and a homeomorphism
and a homeomorphism 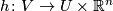
which makes the following diagram commute:
![\displaystyle \xymatrix{& V \ar[dr]^{j|_V} \ar[dd]^h \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}}.](/images/math/9/2/8/92848a11983524dd53282be31bba8921.png)
The space  is called the total space of the bundle and
is called the total space of the bundle and  the base space.
the base space.
Two microbundles 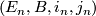 ,
, 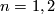 over the same space
over the same space  are isomorphic if there exist neighbourhoods
are isomorphic if there exist neighbourhoods 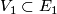 of
of 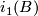 and
and 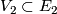 of
of 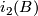 and a homeomorphism
and a homeomorphism 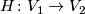 making the following diagram commute:
making the following diagram commute:
![\displaystyle \xymatrix{ & V_1 \ar[dd]^{H} \ar[dr]^{j_1|_{V_1}} \\ B \ar[ur]^{i_1} \ar[dr]_{i_2} & & B \\ & V_2 \ar[ur]_{j_2|_{V_2}} }](/images/math/6/5/0/650cf2c11076ca7ab0a7ba68e744a9fa.png)
2 Examples
An important example of a microbundle is the tangent microbundle of a topological (or similarly  ) manifold
) manifold  .
Let
.
Let
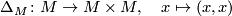
be the diagonal map for  .
.
Example 2.1 [Milnor1964, Lemma 2.1].
Let  be topological (or PL)
be topological (or PL)  -manifold, and let
-manifold, and let 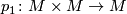 be the projection onto the first factor. Then
be the projection onto the first factor. Then
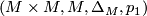
is an  -dimensional microbundle, the tangent microbundle
-dimensional microbundle, the tangent microbundle 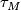 of
of  .
.
Remark 2.2.
An atlas of  gives a product atlas of
gives a product atlas of 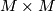 which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold
which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold  in
in 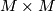 is isomorphic to its tangent bundle.
is isomorphic to its tangent bundle.
Another important example of a microbundle is the micro-bundle defined by a topological topological  -bundle.
-bundle.
Example 2.3. Let 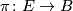 be a topological
be a topological  -bundle with zero section
-bundle with zero section 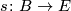 . Then the quadruple
. Then the quadruple
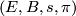
is an  -dimensional microbundle.
-dimensional microbundle.
3 The Kister-Mazur Theorem
A fundamental fact about microbundles is the following theorem, often called the Kister-Mazur theorem, proven independently by Kister and Mazur.
Theorem 3.1 [Kister1964, Theorem 2].
Let 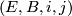 be an
be an  -dimensional microbundle over a locally finite, finite dimensional simplicial complex
-dimensional microbundle over a locally finite, finite dimensional simplicial complex  .
Then there is a neighbourhood of
.
Then there is a neighbourhood of 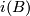 ,
, 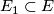 such that the following hold.
such that the following hold.
-
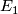 is the total space of a topological
is the total space of a topological  -bundle over
-bundle over  .
.
-
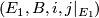 is a microbundle and the the inclusion
is a microbundle and the the inclusion 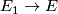 is a microbundle isomorphism.
is a microbundle isomorphism.
- If
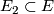 is any other such neighbourhood of
is any other such neighbourhood of 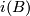 then there is a
then there is a  -bundle isomorphism
-bundle isomorphism 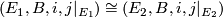 .
.
Remark 3.2.
Microbundle theory is an important part of the work by Kirby and Siebenmann [Kirby&Siebenmann1977] on smooth structures and  -structures on higher dimensional topological manifolds.
-structures on higher dimensional topological manifolds.
4 References
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404
5 External links
- The Wikipedia page about microbundles.
 -bundle; i.e. a fibre bundle with structure group the homeomorphisms of
-bundle; i.e. a fibre bundle with structure group the homeomorphisms of  fixing
fixing  .
.
Definition 1.1 [Milnor1964] .
Let  be a topological space. An
be a topological space. An  -dimensional microbundle over
-dimensional microbundle over  is a quadruple
is a quadruple 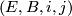 where
where  is a space,
is a space,  and
and  are maps fitting into the following diagram
are maps fitting into the following diagram
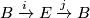
and the following conditions hold:
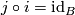 .
.
- For all
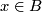 there exist open neigbourhood
there exist open neigbourhood  , an open neighbourhood
, an open neighbourhood  of
of 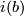 and a homeomorphism
and a homeomorphism 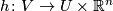
which makes the following diagram commute:
![\displaystyle \xymatrix{& V \ar[dr]^{j|_V} \ar[dd]^h \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}}.](/images/math/9/2/8/92848a11983524dd53282be31bba8921.png)
The space  is called the total space of the bundle and
is called the total space of the bundle and  the base space.
the base space.
Two microbundles 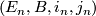 ,
, 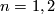 over the same space
over the same space  are isomorphic if there exist neighbourhoods
are isomorphic if there exist neighbourhoods 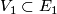 of
of 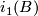 and
and 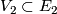 of
of 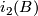 and a homeomorphism
and a homeomorphism 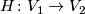 making the following diagram commute:
making the following diagram commute:
![\displaystyle \xymatrix{ & V_1 \ar[dd]^{H} \ar[dr]^{j_1|_{V_1}} \\ B \ar[ur]^{i_1} \ar[dr]_{i_2} & & B \\ & V_2 \ar[ur]_{j_2|_{V_2}} }](/images/math/6/5/0/650cf2c11076ca7ab0a7ba68e744a9fa.png)
2 Examples
An important example of a microbundle is the tangent microbundle of a topological (or similarly  ) manifold
) manifold  .
Let
.
Let
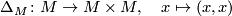
be the diagonal map for  .
.
Example 2.1 [Milnor1964, Lemma 2.1].
Let  be topological (or PL)
be topological (or PL)  -manifold, and let
-manifold, and let 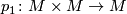 be the projection onto the first factor. Then
be the projection onto the first factor. Then
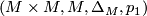
is an  -dimensional microbundle, the tangent microbundle
-dimensional microbundle, the tangent microbundle 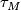 of
of  .
.
Remark 2.2.
An atlas of  gives a product atlas of
gives a product atlas of 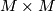 which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold
which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold  in
in 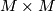 is isomorphic to its tangent bundle.
is isomorphic to its tangent bundle.
Another important example of a microbundle is the micro-bundle defined by a topological topological  -bundle.
-bundle.
Example 2.3. Let 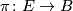 be a topological
be a topological  -bundle with zero section
-bundle with zero section 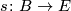 . Then the quadruple
. Then the quadruple
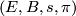
is an  -dimensional microbundle.
-dimensional microbundle.
3 The Kister-Mazur Theorem
A fundamental fact about microbundles is the following theorem, often called the Kister-Mazur theorem, proven independently by Kister and Mazur.
Theorem 3.1 [Kister1964, Theorem 2].
Let 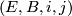 be an
be an  -dimensional microbundle over a locally finite, finite dimensional simplicial complex
-dimensional microbundle over a locally finite, finite dimensional simplicial complex  .
Then there is a neighbourhood of
.
Then there is a neighbourhood of 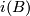 ,
, 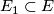 such that the following hold.
such that the following hold.
-
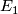 is the total space of a topological
is the total space of a topological  -bundle over
-bundle over  .
.
-
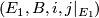 is a microbundle and the the inclusion
is a microbundle and the the inclusion 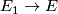 is a microbundle isomorphism.
is a microbundle isomorphism.
- If
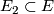 is any other such neighbourhood of
is any other such neighbourhood of 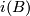 then there is a
then there is a  -bundle isomorphism
-bundle isomorphism 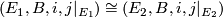 .
.
Remark 3.2.
Microbundle theory is an important part of the work by Kirby and Siebenmann [Kirby&Siebenmann1977] on smooth structures and  -structures on higher dimensional topological manifolds.
-structures on higher dimensional topological manifolds.
4 References
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404
5 External links
- The Wikipedia page about microbundles.