Manifold Atlas:Definition of “manifold”
(→Riemannian Manifolds) |
|||
| Line 37: | Line 37: | ||
A Riemannian metric $g$ on a smooth manifold $M$ is a smooth family of scalar products | A Riemannian metric $g$ on a smooth manifold $M$ is a smooth family of scalar products | ||
$$ g_x : T_xM \times T_xM \longmapsto \Rr$$ | $$ g_x : T_xM \times T_xM \longmapsto \Rr$$ | ||
| − | defined on the tangent spaces $T_xM$ for each $x$ in $M$. This means that for each | + | defined on the [[Wikipedia:Tangent_space|tangent spaces]] $T_xM$ for each $x$ in $M$. This means that for each pair of smooth [[Wikipedia:Vector_field|vector fields]] $v_1$ and $v_2$ on $M$ the map |
$$ M \to \Rr, ~~~ x \longmapsto g_x(v_1(x),v_2(x))$$ | $$ M \to \Rr, ~~~ x \longmapsto g_x(v_1(x),v_2(x))$$ | ||
is smooth. | is smooth. | ||
Revision as of 16:02, 21 September 2009
1 Introduction
This page defines the term “manifold” as used in the Manifold Atlas. We assume that all manifolds are of a fixed dimension n.
Definition 1.1.
An n-dimensional manifold  is a second countable Hausdorff space for which every point
is a second countable Hausdorff space for which every point 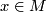 has a neighbourhood
has a neighbourhood 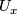 homeomorphic to an open subset of
homeomorphic to an open subset of 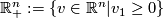 .
.
- The interior of
 , denoted
, denoted 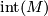 , is the subset of points for which
, is the subset of points for which 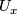 is an open subset of
is an open subset of 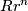 .
.
- The boundary of
 , written
, written 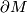 , is the complement of the interior of
, is the complement of the interior of  .
.
-
 is called closed if
is called closed if  is compact and
is compact and 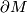 is empty.
is empty.
A manifold  as above is often called a topological manifold for emphasis or clarity.
Typically, but not necessarly, the word “manifold” will mean "topological manifold with extra structure", be it piecewise-linear, smooth, complex, symplectic, contact, Riemannian, etc. The extra structure will be emphasised or suppressed in notation and vocabulary as is appropriate. We briefly review some common categories of manifolds below.
as above is often called a topological manifold for emphasis or clarity.
Typically, but not necessarly, the word “manifold” will mean "topological manifold with extra structure", be it piecewise-linear, smooth, complex, symplectic, contact, Riemannian, etc. The extra structure will be emphasised or suppressed in notation and vocabulary as is appropriate. We briefly review some common categories of manifolds below.
2 Atlases of charts
We give a unified presentation of piecewise linear, smooth and complex manifolds. In the complex case, we assume that the dimension is even and that the dimension is even.
Recall that a chart on a topological manifold  is a homeomporphism
is a homeomporphism 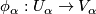 from an open subset
from an open subset 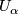 of
of  to an open subset
to an open subset 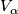 of
of 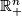 . The transition function defined by two charts
. The transition function defined by two charts 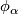 and
and 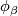 is the homeomorphism
is the homeomorphism
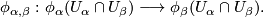
An atlas for  is a collection of charts
is a collection of charts 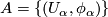 such that the
such that the 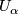 cover
cover  .
.
Let 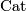 denote either the piecewise linear, smooth or complex categories where by “smooth" we indicate
denote either the piecewise linear, smooth or complex categories where by “smooth" we indicate 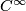 maps. That is we require every
maps. That is we require every 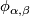 to be either piecewise linear, smooth of class
to be either piecewise linear, smooth of class 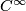 or holomorphic. An atlas is a
or holomorphic. An atlas is a 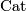 Atlas if every transition function defined by the that atlas is a
Atlas if every transition function defined by the that atlas is a 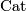 function.
function. 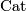 atlases are compatible if their union again forms a
atlases are compatible if their union again forms a 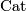 atlas and by Zorn's Lemma each
atlas and by Zorn's Lemma each 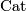 atlas defines a unique maximal
atlas defines a unique maximal 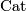 atlas.
atlas.
Definition 2.1. A 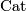 -manifold
-manifold 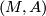 is a manifold
is a manifold  together with a maximal
together with a maximal 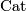 atlas
atlas  .
.
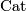 -isomorphism
-isomorphism 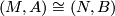 is a homeomorphism
is a homeomorphism 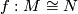 which is a
which is a 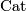 morphism when viewed in every pair of charts in
morphism when viewed in every pair of charts in  and
and  .
.3 Riemannian Manifolds
A Riemannian metric  on a smooth manifold
on a smooth manifold  is a smooth family of scalar products
is a smooth family of scalar products
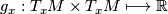
defined on the tangent spaces 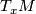 for each
for each  in
in  . This means that for each pair of smooth vector fields
. This means that for each pair of smooth vector fields 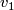 and
and 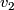 on
on  the map
the map
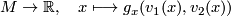
is smooth.
Definition 3.1.
A Riemannian manifold 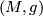 is a smooth manifold
is a smooth manifold  together with a Riemannian metric
together with a Riemannian metric  .
.
An isometry between Riemannian manifolds is a diffeomorphism whose differential preserves the metric  .
.