Links of singular points of complex hypersurfaces
m (→Further discussion) |
m (→Invariants) |
||
| (3 intermediate revisions by one user not shown) | |||
| Line 13: | Line 13: | ||
Near a regular point $z$, the complex hypersurface $V$ is a smooth manifold of real dimension $2n$; in a small neighborhood of a singular point $z$, the topology of the complex hypersurface $V$ is more complicated. One way to look at the topology near $z$, due to Brauner, is to look at the intersection of $V$ with a $(2n+1)$-dimensioanl sphere of small radius $\epsilon$ $S_{\epsilon}$ centered at $z$. | Near a regular point $z$, the complex hypersurface $V$ is a smooth manifold of real dimension $2n$; in a small neighborhood of a singular point $z$, the topology of the complex hypersurface $V$ is more complicated. One way to look at the topology near $z$, due to Brauner, is to look at the intersection of $V$ with a $(2n+1)$-dimensioanl sphere of small radius $\epsilon$ $S_{\epsilon}$ centered at $z$. | ||
| − | \begin{ | + | \begin{theorem} |
The space $K=V\cap S_{\epsilon}$ is $(n-2)$-connected. | The space $K=V\cap S_{\epsilon}$ is $(n-2)$-connected. | ||
| − | \end{ | + | \end{theorem} |
The homeomorphism type of $K$ is independent of the small parameter $\epsilon$, it is called the '''link''' of the singular point $z$. | The homeomorphism type of $K$ is independent of the small parameter $\epsilon$, it is called the '''link''' of the singular point $z$. | ||
| − | \begin{ | + | \begin{theorem}(Fibration Theorem)\label{fibration} |
For $\epsilon$ sufficiently small, the space $S_{\epsilon}-K$ is a smooth fiber bundle over $S^1$, with projection map $\phi \colon S_{\epsilon}-K \to S^1$, $z \mapsto f(z)/|f(z)|$. Each fiber $F_{\theta}$ is parallelizable and has the homotopy type of a finite CW-complex of dimension $n$. | For $\epsilon$ sufficiently small, the space $S_{\epsilon}-K$ is a smooth fiber bundle over $S^1$, with projection map $\phi \colon S_{\epsilon}-K \to S^1$, $z \mapsto f(z)/|f(z)|$. Each fiber $F_{\theta}$ is parallelizable and has the homotopy type of a finite CW-complex of dimension $n$. | ||
| − | \end{ | + | \end{theorem} |
The fiber $F_{\theta}$ is usually called the '''Milnor fiber''' of the singular point $z$. | The fiber $F_{\theta}$ is usually called the '''Milnor fiber''' of the singular point $z$. | ||
| Line 29: | Line 29: | ||
In this special situation, the above theorems are strengthened to the following | In this special situation, the above theorems are strengthened to the following | ||
| − | \begin{ | + | \begin{theorem} |
Each fiber $F_{\theta}$ is a smooth parallelizable manifold, the closure $\overline{F_{\theta}}$ has boundary $K$ and the homotopy type of a bouquet of $n$-spheres $S^n\vee \cdots \vee S^n$. | Each fiber $F_{\theta}$ is a smooth parallelizable manifold, the closure $\overline{F_{\theta}}$ has boundary $K$ and the homotopy type of a bouquet of $n$-spheres $S^n\vee \cdots \vee S^n$. | ||
| − | \end{ | + | \end{theorem} |
</wikitex> | </wikitex> | ||
| Line 42: | Line 42: | ||
Let $V$ be a complex hypersurface defined by $f(z_1, \dots, z_{n+1})$, $z^0$ be an isolated singular point of $V$. Let $g_j=\partial f /\partial z_j$ $j=1, \dots, n+1$. By putting all these $g_j$'s together we get the gradient field of $f$, which can be viewed as a map $g \colon \mathbb C^{n+1} \to \mathbb C^{n+1}$, $z \mapsto (g_1(z), \dots, g_{n+1}(z))$. If $z^0$ is an isolated singular point, then $z \mapsto g(z)/||g(z)||$ is a well-defined map from a small sphere $S_{\epsilon}$ centered at $z^0$ to the unit sphere $S^{2n+1}$ of $\mathbb C^{n+1}$. The mapping degree $\mu$ is called the multiplicity of the isolated singular point $z^0$. ($\mu$ is also called the Milnor number of $z^0$.) | Let $V$ be a complex hypersurface defined by $f(z_1, \dots, z_{n+1})$, $z^0$ be an isolated singular point of $V$. Let $g_j=\partial f /\partial z_j$ $j=1, \dots, n+1$. By putting all these $g_j$'s together we get the gradient field of $f$, which can be viewed as a map $g \colon \mathbb C^{n+1} \to \mathbb C^{n+1}$, $z \mapsto (g_1(z), \dots, g_{n+1}(z))$. If $z^0$ is an isolated singular point, then $z \mapsto g(z)/||g(z)||$ is a well-defined map from a small sphere $S_{\epsilon}$ centered at $z^0$ to the unit sphere $S^{2n+1}$ of $\mathbb C^{n+1}$. The mapping degree $\mu$ is called the multiplicity of the isolated singular point $z^0$. ($\mu$ is also called the Milnor number of $z^0$.) | ||
| − | \begin{ | + | \begin{theorem} |
The middle homology group $H_n(F_{\theta})$ is a free abelian group of rank $\mu$. | The middle homology group $H_n(F_{\theta})$ is a free abelian group of rank $\mu$. | ||
| − | \end{ | + | \end{theorem} |
Furthermore, the homology groups of the link $K$ are determined from the long homology exact sequence | Furthermore, the homology groups of the link $K$ are determined from the long homology exact sequence | ||
| Line 52: | Line 52: | ||
A symmetric or skew symmetric bilinear form on a free abelian group is usually referred to as a lattice. $s$ is called the '''Milnor lattice''' of the singular point. Thus the homology groups of the link $K$ is completely determined by the Milnor lattice of the singular point. | A symmetric or skew symmetric bilinear form on a free abelian group is usually referred to as a lattice. $s$ is called the '''Milnor lattice''' of the singular point. Thus the homology groups of the link $K$ is completely determined by the Milnor lattice of the singular point. | ||
</wikitex> | </wikitex> | ||
| + | |||
== Topological spheres as links of singular points == | == Topological spheres as links of singular points == | ||
<wikitex>; | <wikitex>; | ||
Latest revision as of 12:54, 14 January 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
The links of singular points of complex hypersurfaces provide a large class of examples of highly-connected odd dimensional manifolds. A standard reference is [Milnor1968]. See also [Hirzebruch&Mayer1968] and [Dimca1992].
These manifolds are the boundaries of highly-connected, stably parallelisable even dimensional manifolds and hence stably parallelisable themselves. In the case of singular points of complex curves, the link of such a singular point is a fibered link in the  -dimensional sphere
-dimensional sphere  .
.
[edit] 2 Construction and properties
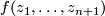 be a non-constant polynomial in
be a non-constant polynomial in 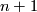 complex variables. A complex hypersurface
complex variables. A complex hypersurface Tex syntax erroris the algebraic set consisting of points
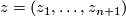 such that
such that 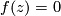 . A regular point
. A regular point 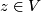 is a point at which some partial derivative
is a point at which some partial derivative 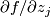 does not vanish; if at a point
does not vanish; if at a point 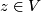 all the partial derivatives
all the partial derivatives 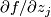 vanish,
vanish,  is called a singular point of
is called a singular point of Tex syntax error. Near a regular point
 , the complex hypersurface
, the complex hypersurface Tex syntax erroris a smooth manifold of real dimension
 ; in a small neighborhood of a singular point
; in a small neighborhood of a singular point  , the topology of the complex hypersurface
, the topology of the complex hypersurface Tex syntax erroris more complicated. One way to look at the topology near
 , due to Brauner, is to look at the intersection of
, due to Brauner, is to look at the intersection of Tex syntax errorwith a
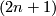 -dimensioanl sphere of small radius
-dimensioanl sphere of small radius 
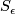 centered at
centered at  .
.
Theorem 2.1.
The space 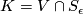 is
is  -connected.
-connected.
The homeomorphism type of  is independent of the small parameter
is independent of the small parameter  , it is called the link of the singular point
, it is called the link of the singular point  .
.
Theorem 2.2.(Fibration Theorem)
For  sufficiently small, the space
sufficiently small, the space 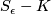 is a smooth fiber bundle over
is a smooth fiber bundle over  , with projection map
, with projection map 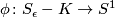 ,
, 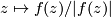 . Each fiber
. Each fiber 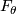 is parallelizable and has the homotopy type of a finite CW-complex of dimension
is parallelizable and has the homotopy type of a finite CW-complex of dimension  .
.
The fiber 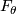 is usually called the Milnor fiber of the singular point
is usually called the Milnor fiber of the singular point  .
.
A singular point  is isolated if there is no other singular point in some small neighborhood of
is isolated if there is no other singular point in some small neighborhood of  .
.
In this special situation, the above theorems are strengthened to the following
Theorem 2.3.
Each fiber 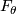 is a smooth parallelizable manifold, the closure
is a smooth parallelizable manifold, the closure 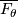 has boundary
has boundary  and the homotopy type of a bouquet of
and the homotopy type of a bouquet of  -spheres
-spheres 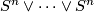 .
.
[edit] 3 Invariants
 of an isolated singular point
of an isolated singular point  of a complex hypersurface
of a complex hypersurface Tex syntax errorof complex dimension
 is an
is an  -connected
-connected 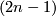 -dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a
-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a 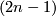 -dimensional closed manifold
-dimensional closed manifold  which is not a homotopy sphere,
which is not a homotopy sphere,  is the highest connectivity
is the highest connectivity  could have. Therefore to understand the classification and invariants of the links
could have. Therefore to understand the classification and invariants of the links  one needs to understand the classification and invariants of highly-connected odd dimensional manifolds.
one needs to understand the classification and invariants of highly-connected odd dimensional manifolds.
On the other hand, as the link  is closely related to the singular point
is closely related to the singular point  of the complex hypersurfaces, some of the topological invariants of
of the complex hypersurfaces, some of the topological invariants of  are computable from the polynomial.
are computable from the polynomial.
Tex syntax errorbe a complex hypersurface defined by
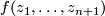 ,
, 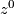 be an isolated singular point of
be an isolated singular point of Tex syntax error. Let
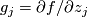
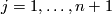 . By putting all these
. By putting all these 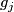 's together we get the gradient field of
's together we get the gradient field of  , which can be viewed as a map
, which can be viewed as a map 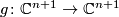 ,
, 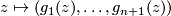 . If
. If 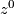 is an isolated singular point, then
is an isolated singular point, then 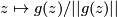 is a well-defined map from a small sphere
is a well-defined map from a small sphere 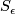 centered at
centered at 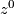 to the unit sphere
to the unit sphere 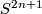 of
of 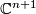 . The mapping degree
. The mapping degree  is called the multiplicity of the isolated singular point
is called the multiplicity of the isolated singular point 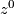 . (
. ( is also called the Milnor number of
is also called the Milnor number of 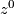 .)
.)
Theorem 3.1.
The middle homology group 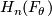 is a free abelian group of rank
is a free abelian group of rank  .
.
Furthermore, the homology groups of the link  are determined from the long homology exact sequence
are determined from the long homology exact sequence
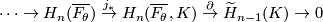
of the pair 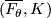 . The map
. The map 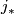 is the adjoint of the intersection pairing on
is the adjoint of the intersection pairing on 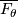
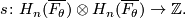
A symmetric or skew symmetric bilinear form on a free abelian group is usually referred to as a lattice.  is called the Milnor lattice of the singular point. Thus the homology groups of the link
is called the Milnor lattice of the singular point. Thus the homology groups of the link  is completely determined by the Milnor lattice of the singular point.
is completely determined by the Milnor lattice of the singular point.
[edit] 4 Topological spheres as links of singular points
Especially, the link  is an integral homology sphere if and only if the intersection form
is an integral homology sphere if and only if the intersection form  is unimodular, i.~e.~the matrix of
is unimodular, i.~e.~the matrix of  has determinant
has determinant 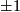 . If
. If 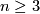 , the Generalized Poincare Conjecture implies that
, the Generalized Poincare Conjecture implies that  is a topological sphere.
is a topological sphere.
By Theorem 2.2, there is a smooth fiber bundle over  with fiber
with fiber 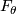 . The natural action of a generator of
. The natural action of a generator of 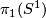 induces the characteristic homeomorphism
induces the characteristic homeomorphism  of the fiber
of the fiber 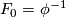 . Let
. Let 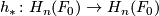 be the induced isomorphism on homology and
be the induced isomorphism on homology and  be the characteristic polynomial of the linear transformation
be the characteristic polynomial of the linear transformation 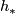 . It's a consequence of the Wang sequence associated with the fiber bundle over
. It's a consequence of the Wang sequence associated with the fiber bundle over  that
that
Lemma 4.1.
For 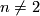 the manifolds
the manifolds  is a topological sphere is and only if the integer
is a topological sphere is and only if the integer  equals to
equals to 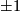 .
.
When  is a topological sphere, as it is the boundary of an
is a topological sphere, as it is the boundary of an  -connected parallelisable
-connected parallelisable  -manifold
-manifold 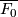 , our knowledge of exotic spheres allows us to determine the diffeomorphism class of
, our knowledge of exotic spheres allows us to determine the diffeomorphism class of  completely:
completely:
- if
 is even, the diffeomorphism class of
is even, the diffeomorphism class of  is determined by the signature of the intersection pairing
is determined by the signature of the intersection pairing
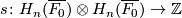
- if
 is odd, the diffeomorphism class of
is odd, the diffeomorphism class of  is determined by the Kervaire invariant
is determined by the Kervaire invariant
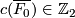
which was computed in [Levine1966]
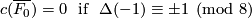
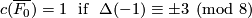
[edit] 5 Examples
The Brieskorn singularitites is a class of singular points which have been extensively studied. These are defined by the polynomials of the form
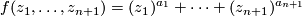
where 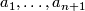 are integers
are integers 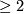 . The origin is an isolated singular point of
. The origin is an isolated singular point of  .
.
\begin{thm}(Brieskorn-Pham)
The group 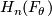 is free abelian of rank
is free abelian of rank
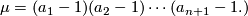
The characteristic polynomial is
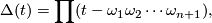
where each 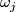 ranges over all
ranges over all 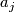 -th root of unit other than
-th root of unit other than  .
\end{thm}
.
\end{thm}
The link  is called a Brieskorn variety.
is called a Brieskorn variety.
For 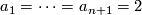 , it's seen from the defining equations that the link
, it's seen from the defining equations that the link  is the sphere bundle of the tangent bundle of the
is the sphere bundle of the tangent bundle of the  -sphere, i.~e.~the Stiefel manifold
-sphere, i.~e.~the Stiefel manifold 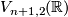 .
.
The simplest nontrivial example is 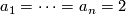 ,
, 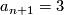 . Then
. Then 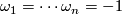 ,
, 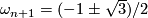 . The characteristic polynomial is
. The characteristic polynomial is
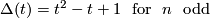
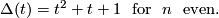
For 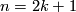 we have
we have 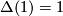 so the link
so the link  is a topological sphere of dimension
is a topological sphere of dimension 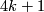 ;
; 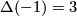 , thus by [Levine1966]
, thus by [Levine1966]  has nontrivial Kervaire invariant.
Especially for
has nontrivial Kervaire invariant.
Especially for 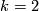
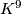 is the Kervaire sphere.
is the Kervaire sphere.
The above example is a special case of the 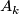 -singularities, whose defining polynomial is
-singularities, whose defining polynomial is
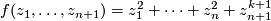
 being an integer
being an integer 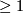 . The Milnor lattice of an
. The Milnor lattice of an 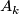 -singularity is represented by the Dynkin diagram of the simple Lie algebra
-singularity is represented by the Dynkin diagram of the simple Lie algebra 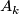 . When
. When  , the diffeomorphism classification of the link
, the diffeomorphism classification of the link  is obtained from its Milnor lattice and the classification of simply-connected 5-manifolds:
is obtained from its Milnor lattice and the classification of simply-connected 5-manifolds:
-
 is diffeomorphic to
is diffeomorphic to 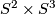 if
if  is odd;
is odd;
-
 is diffeomorphic to
is diffeomorphic to 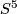 if
if  is even.
is even.
In this dimension, the diffeomorphism classification of the link  of other types of singular points can be obtained in the same way, once we know the Milnor lattice of the singular point.
of other types of singular points can be obtained in the same way, once we know the Milnor lattice of the singular point.
[edit] 6 Further discussion
 of a singular point
of a singular point  is the intersection of the hypersurface
is the intersection of the hypersurface Tex syntax errordefined by
 and the sphere
and the sphere 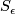 in the ambient space
in the ambient space 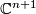 . Therefore it inherits certain symmetries from that of the singular point. As an example, consider an
. Therefore it inherits certain symmetries from that of the singular point. As an example, consider an 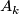 -singularity in
-singularity in 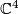 . There is an orientation preserving involution
. There is an orientation preserving involution
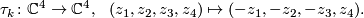
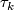 induces an orientation preserving free involution of
induces an orientation preserving free involution of 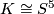 or
or 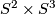 . For
. For 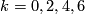 ,
, 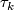 's provide all the 4 smooth free involutions on
's provide all the 4 smooth free involutions on 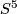 (see [Geiges&Thomas1998]).
(see [Geiges&Thomas1998]).
[edit] 7 References
- [Dimca1992] A. Dimca, Singularities and topology of hypersurfaces, Springer-Verlag, New York, 1992. MR1194180 (94b:32058) Zbl 0753.57001
- [Geiges&Thomas1998] H. Geiges and C. B. Thomas, Contact topology and the structure of
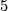 -manifolds with
-manifolds with 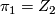 , Ann. Inst. Fourier (Grenoble) 48 (1998), no.4, 1167–1188. MR1656012 (2000a:57069) Zbl 0912.57020
, Ann. Inst. Fourier (Grenoble) 48 (1998), no.4, 1167–1188. MR1656012 (2000a:57069) Zbl 0912.57020
- [Hirzebruch&Mayer1968] F. Hirzebruch and K. H. Mayer,
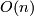 -Mannigfaltigkeiten, exotische Sphären und Singularitäten, Springer-Verlag, Berlin, 1968. MR0229251 (37 #4825) Zbl 0172.25304
-Mannigfaltigkeiten, exotische Sphären und Singularitäten, Springer-Verlag, Berlin, 1968. MR0229251 (37 #4825) Zbl 0172.25304
- [Levine1966] J. Levine, Polynomial invariants of knots of codimension two, Ann. of Math. (2) 84 (1966), 537–554. MR0200922 (34 #808) Zbl 0196.55905
- [Milnor1968] J. Milnor, Singular points of complex hypersurfaces, Princeton University Press, Princeton, N.J., 1968. MR0239612 (39 #969) Zbl 0224.57014
 .
.
[edit] 2 Construction and properties
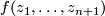 be a non-constant polynomial in
be a non-constant polynomial in 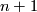 complex variables. A complex hypersurface
complex variables. A complex hypersurface Tex syntax erroris the algebraic set consisting of points
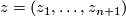 such that
such that 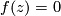 . A regular point
. A regular point 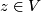 is a point at which some partial derivative
is a point at which some partial derivative 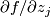 does not vanish; if at a point
does not vanish; if at a point 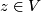 all the partial derivatives
all the partial derivatives 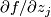 vanish,
vanish,  is called a singular point of
is called a singular point of Tex syntax error. Near a regular point
 , the complex hypersurface
, the complex hypersurface Tex syntax erroris a smooth manifold of real dimension
 ; in a small neighborhood of a singular point
; in a small neighborhood of a singular point  , the topology of the complex hypersurface
, the topology of the complex hypersurface Tex syntax erroris more complicated. One way to look at the topology near
 , due to Brauner, is to look at the intersection of
, due to Brauner, is to look at the intersection of Tex syntax errorwith a
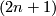 -dimensioanl sphere of small radius
-dimensioanl sphere of small radius 
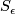 centered at
centered at  .
.
Theorem 2.1.
The space 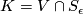 is
is  -connected.
-connected.
The homeomorphism type of  is independent of the small parameter
is independent of the small parameter  , it is called the link of the singular point
, it is called the link of the singular point  .
.
Theorem 2.2.(Fibration Theorem)
For  sufficiently small, the space
sufficiently small, the space 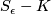 is a smooth fiber bundle over
is a smooth fiber bundle over  , with projection map
, with projection map 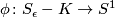 ,
, 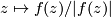 . Each fiber
. Each fiber 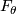 is parallelizable and has the homotopy type of a finite CW-complex of dimension
is parallelizable and has the homotopy type of a finite CW-complex of dimension  .
.
The fiber 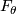 is usually called the Milnor fiber of the singular point
is usually called the Milnor fiber of the singular point  .
.
A singular point  is isolated if there is no other singular point in some small neighborhood of
is isolated if there is no other singular point in some small neighborhood of  .
.
In this special situation, the above theorems are strengthened to the following
Theorem 2.3.
Each fiber 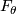 is a smooth parallelizable manifold, the closure
is a smooth parallelizable manifold, the closure 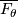 has boundary
has boundary  and the homotopy type of a bouquet of
and the homotopy type of a bouquet of  -spheres
-spheres 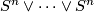 .
.
[edit] 3 Invariants
 of an isolated singular point
of an isolated singular point  of a complex hypersurface
of a complex hypersurface Tex syntax errorof complex dimension
 is an
is an  -connected
-connected 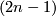 -dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a
-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a 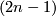 -dimensional closed manifold
-dimensional closed manifold  which is not a homotopy sphere,
which is not a homotopy sphere,  is the highest connectivity
is the highest connectivity  could have. Therefore to understand the classification and invariants of the links
could have. Therefore to understand the classification and invariants of the links  one needs to understand the classification and invariants of highly-connected odd dimensional manifolds.
one needs to understand the classification and invariants of highly-connected odd dimensional manifolds.
On the other hand, as the link  is closely related to the singular point
is closely related to the singular point  of the complex hypersurfaces, some of the topological invariants of
of the complex hypersurfaces, some of the topological invariants of  are computable from the polynomial.
are computable from the polynomial.
Tex syntax errorbe a complex hypersurface defined by
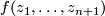 ,
, 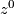 be an isolated singular point of
be an isolated singular point of Tex syntax error. Let
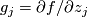
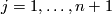 . By putting all these
. By putting all these 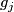 's together we get the gradient field of
's together we get the gradient field of  , which can be viewed as a map
, which can be viewed as a map 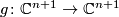 ,
, 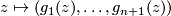 . If
. If 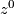 is an isolated singular point, then
is an isolated singular point, then 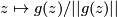 is a well-defined map from a small sphere
is a well-defined map from a small sphere 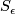 centered at
centered at 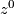 to the unit sphere
to the unit sphere 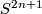 of
of 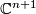 . The mapping degree
. The mapping degree  is called the multiplicity of the isolated singular point
is called the multiplicity of the isolated singular point 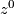 . (
. ( is also called the Milnor number of
is also called the Milnor number of 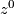 .)
.)
Theorem 3.1.
The middle homology group 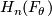 is a free abelian group of rank
is a free abelian group of rank  .
.
Furthermore, the homology groups of the link  are determined from the long homology exact sequence
are determined from the long homology exact sequence
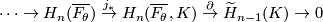
of the pair 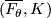 . The map
. The map 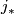 is the adjoint of the intersection pairing on
is the adjoint of the intersection pairing on 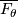
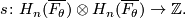
A symmetric or skew symmetric bilinear form on a free abelian group is usually referred to as a lattice.  is called the Milnor lattice of the singular point. Thus the homology groups of the link
is called the Milnor lattice of the singular point. Thus the homology groups of the link  is completely determined by the Milnor lattice of the singular point.
is completely determined by the Milnor lattice of the singular point.
[edit] 4 Topological spheres as links of singular points
Especially, the link  is an integral homology sphere if and only if the intersection form
is an integral homology sphere if and only if the intersection form  is unimodular, i.~e.~the matrix of
is unimodular, i.~e.~the matrix of  has determinant
has determinant 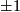 . If
. If 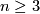 , the Generalized Poincare Conjecture implies that
, the Generalized Poincare Conjecture implies that  is a topological sphere.
is a topological sphere.
By Theorem 2.2, there is a smooth fiber bundle over  with fiber
with fiber 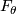 . The natural action of a generator of
. The natural action of a generator of 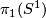 induces the characteristic homeomorphism
induces the characteristic homeomorphism  of the fiber
of the fiber 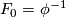 . Let
. Let 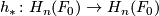 be the induced isomorphism on homology and
be the induced isomorphism on homology and  be the characteristic polynomial of the linear transformation
be the characteristic polynomial of the linear transformation 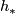 . It's a consequence of the Wang sequence associated with the fiber bundle over
. It's a consequence of the Wang sequence associated with the fiber bundle over  that
that
Lemma 4.1.
For 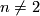 the manifolds
the manifolds  is a topological sphere is and only if the integer
is a topological sphere is and only if the integer  equals to
equals to 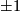 .
.
When  is a topological sphere, as it is the boundary of an
is a topological sphere, as it is the boundary of an  -connected parallelisable
-connected parallelisable  -manifold
-manifold 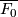 , our knowledge of exotic spheres allows us to determine the diffeomorphism class of
, our knowledge of exotic spheres allows us to determine the diffeomorphism class of  completely:
completely:
- if
 is even, the diffeomorphism class of
is even, the diffeomorphism class of  is determined by the signature of the intersection pairing
is determined by the signature of the intersection pairing
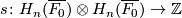
- if
 is odd, the diffeomorphism class of
is odd, the diffeomorphism class of  is determined by the Kervaire invariant
is determined by the Kervaire invariant
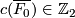
which was computed in [Levine1966]
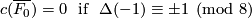
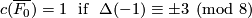
[edit] 5 Examples
The Brieskorn singularitites is a class of singular points which have been extensively studied. These are defined by the polynomials of the form
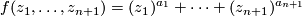
where 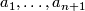 are integers
are integers 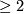 . The origin is an isolated singular point of
. The origin is an isolated singular point of  .
.
\begin{thm}(Brieskorn-Pham)
The group 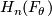 is free abelian of rank
is free abelian of rank
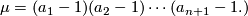
The characteristic polynomial is
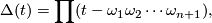
where each 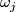 ranges over all
ranges over all 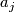 -th root of unit other than
-th root of unit other than  .
\end{thm}
.
\end{thm}
The link  is called a Brieskorn variety.
is called a Brieskorn variety.
For 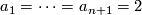 , it's seen from the defining equations that the link
, it's seen from the defining equations that the link  is the sphere bundle of the tangent bundle of the
is the sphere bundle of the tangent bundle of the  -sphere, i.~e.~the Stiefel manifold
-sphere, i.~e.~the Stiefel manifold 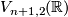 .
.
The simplest nontrivial example is 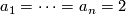 ,
, 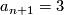 . Then
. Then 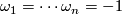 ,
, 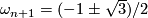 . The characteristic polynomial is
. The characteristic polynomial is
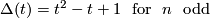
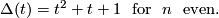
For 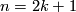 we have
we have 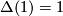 so the link
so the link  is a topological sphere of dimension
is a topological sphere of dimension 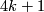 ;
; 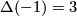 , thus by [Levine1966]
, thus by [Levine1966]  has nontrivial Kervaire invariant.
Especially for
has nontrivial Kervaire invariant.
Especially for 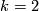
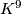 is the Kervaire sphere.
is the Kervaire sphere.
The above example is a special case of the 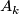 -singularities, whose defining polynomial is
-singularities, whose defining polynomial is
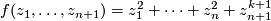
 being an integer
being an integer 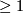 . The Milnor lattice of an
. The Milnor lattice of an 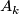 -singularity is represented by the Dynkin diagram of the simple Lie algebra
-singularity is represented by the Dynkin diagram of the simple Lie algebra 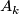 . When
. When  , the diffeomorphism classification of the link
, the diffeomorphism classification of the link  is obtained from its Milnor lattice and the classification of simply-connected 5-manifolds:
is obtained from its Milnor lattice and the classification of simply-connected 5-manifolds:
-
 is diffeomorphic to
is diffeomorphic to 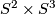 if
if  is odd;
is odd;
-
 is diffeomorphic to
is diffeomorphic to 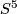 if
if  is even.
is even.
In this dimension, the diffeomorphism classification of the link  of other types of singular points can be obtained in the same way, once we know the Milnor lattice of the singular point.
of other types of singular points can be obtained in the same way, once we know the Milnor lattice of the singular point.
[edit] 6 Further discussion
 of a singular point
of a singular point  is the intersection of the hypersurface
is the intersection of the hypersurface Tex syntax errordefined by
 and the sphere
and the sphere 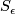 in the ambient space
in the ambient space 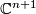 . Therefore it inherits certain symmetries from that of the singular point. As an example, consider an
. Therefore it inherits certain symmetries from that of the singular point. As an example, consider an 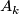 -singularity in
-singularity in 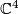 . There is an orientation preserving involution
. There is an orientation preserving involution
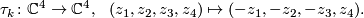
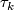 induces an orientation preserving free involution of
induces an orientation preserving free involution of 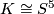 or
or 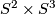 . For
. For 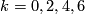 ,
, 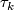 's provide all the 4 smooth free involutions on
's provide all the 4 smooth free involutions on 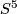 (see [Geiges&Thomas1998]).
(see [Geiges&Thomas1998]).
[edit] 7 References
- [Dimca1992] A. Dimca, Singularities and topology of hypersurfaces, Springer-Verlag, New York, 1992. MR1194180 (94b:32058) Zbl 0753.57001
- [Geiges&Thomas1998] H. Geiges and C. B. Thomas, Contact topology and the structure of
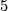 -manifolds with
-manifolds with 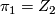 , Ann. Inst. Fourier (Grenoble) 48 (1998), no.4, 1167–1188. MR1656012 (2000a:57069) Zbl 0912.57020
, Ann. Inst. Fourier (Grenoble) 48 (1998), no.4, 1167–1188. MR1656012 (2000a:57069) Zbl 0912.57020
- [Hirzebruch&Mayer1968] F. Hirzebruch and K. H. Mayer,
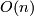 -Mannigfaltigkeiten, exotische Sphären und Singularitäten, Springer-Verlag, Berlin, 1968. MR0229251 (37 #4825) Zbl 0172.25304
-Mannigfaltigkeiten, exotische Sphären und Singularitäten, Springer-Verlag, Berlin, 1968. MR0229251 (37 #4825) Zbl 0172.25304
- [Levine1966] J. Levine, Polynomial invariants of knots of codimension two, Ann. of Math. (2) 84 (1966), 537–554. MR0200922 (34 #808) Zbl 0196.55905
- [Milnor1968] J. Milnor, Singular points of complex hypersurfaces, Princeton University Press, Princeton, N.J., 1968. MR0239612 (39 #969) Zbl 0224.57014