Links of singular points of complex hypersurfaces
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Introduction == | == Introduction == | ||
| − | <wikitex> | + | <wikitex>; |
| − | The links of singular points of complex hypersurfaces | + | The links of singular points of complex hypersurfaces provide a large class of examples of highly-connected odd dimensional manifolds. A standard reference is {{cite|Milnor1968}}. |
| + | These manifolds are the boundaries of [[highly-connected]], [[stably parallelisable]] even dimensional manifolds and hence stably parallelisable themselves. In the case of singular points of complex curves, the link of such a singular point is a fibered link in the $3$-dimensional sphere $S^3$. | ||
</wikitex> | </wikitex> | ||
| Line 42: | Line 31: | ||
Each fiber is a smooth parallelizable manifold with boundary, having the homotopy type of a bouquet of $n$-spheres $S^n\vee \cdots \vee S^n$. | Each fiber is a smooth parallelizable manifold with boundary, having the homotopy type of a bouquet of $n$-spheres $S^n\vee \cdots \vee S^n$. | ||
\end{thm} | \end{thm} | ||
| − | |||
</wikitex> | </wikitex> | ||
| − | == Invariants | + | == Invariants == |
<wikitex>; | <wikitex>; | ||
Seen from the above section, the link $K$ of an isolated singular point $z$ of a complex hypersurface $V$ of complex dimension $n$ is a $(n-2)$-connected $(2n-1)$-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a $(2n-1)$-dimensional closed manifold $M$ which is not a homotopy sphere, $(n-2)$ is the highest connectivity $M$ could have. Therefore to understand the classification and invariants of the links $K$ one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see [[highly-connected_manifolds|highly-connected manifolds]]. | Seen from the above section, the link $K$ of an isolated singular point $z$ of a complex hypersurface $V$ of complex dimension $n$ is a $(n-2)$-connected $(2n-1)$-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a $(2n-1)$-dimensional closed manifold $M$ which is not a homotopy sphere, $(n-2)$ is the highest connectivity $M$ could have. Therefore to understand the classification and invariants of the links $K$ one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see [[highly-connected_manifolds|highly-connected manifolds]]. | ||
| Line 54: | Line 42: | ||
</wikitex> | </wikitex> | ||
| − | == Classification | + | == Classification == |
<wikitex>; | <wikitex>; | ||
... | ... | ||
| Line 66: | Line 54: | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | |||
| − | |||
[[Category:Manifolds]] | [[Category:Manifolds]] | ||
{{Stub}} | {{Stub}} | ||
Revision as of 17:14, 7 June 2010
Contents |
1 Introduction
The links of singular points of complex hypersurfaces provide a large class of examples of highly-connected odd dimensional manifolds. A standard reference is [Milnor1968].
These manifolds are the boundaries of highly-connected, stably parallelisable even dimensional manifolds and hence stably parallelisable themselves. In the case of singular points of complex curves, the link of such a singular point is a fibered link in the  -dimensional sphere
-dimensional sphere  .
.
2 Construction and examples
Let 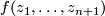 be a non-constant polynomial in
be a non-constant polynomial in 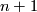 complex variables. A complex hypersurface
complex variables. A complex hypersurface  is the algebraic set consisting of points
is the algebraic set consisting of points 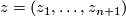 such that
such that 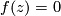 . A regular point
. A regular point 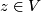 is a point at which some partial derivative
is a point at which some partial derivative 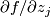 does not vanish; if at a point
does not vanish; if at a point 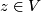 all the partial derivatives
all the partial derivatives 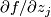 vanish,
vanish,  is called a singular point of
is called a singular point of  .
.
Near a regular point  , the complex hypersurface
, the complex hypersurface  is a smooth manifold of real dimension
is a smooth manifold of real dimension  ; in a small neighborhood of a singular point
; in a small neighborhood of a singular point  , the topology of the complex hypersurface
, the topology of the complex hypersurface  is more complicated. One way to look at the topology near
is more complicated. One way to look at the topology near  , due to Brauner, is to look at the intersection of
, due to Brauner, is to look at the intersection of  with a
with a 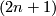 -dimensioanl sphere of small radius
-dimensioanl sphere of small radius 
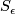 centered at
centered at  .
.
\begin{thm}
The space 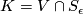 is
is  -connected.
\end{thm}
-connected.
\end{thm}
The topology of  is independent of the small paremeter
is independent of the small paremeter  , it is called the link of the singular point
, it is called the link of the singular point  .
.
\begin{thm}(Fibration Theorem)
For  sufficiently small, the space
sufficiently small, the space 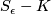 is a smooth fiber bundle over
is a smooth fiber bundle over  , with projection map
, with projection map 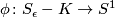 ,
, 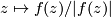 . Each fiber
. Each fiber 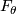 is parallelizable and has the homotopy type of a finite CW-complex of dimension
is parallelizable and has the homotopy type of a finite CW-complex of dimension  .
\end{thm}
.
\end{thm}
The fiber 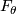 is usually called the Milnor fiber of the singular point
is usually called the Milnor fiber of the singular point  .
.
A singular point  is isolated if there is no other singular point in some small neighborhood of
is isolated if there is no other singular point in some small neighborhood of  .
.
In this special situation, the above theorems are strengthened to the following
\begin{thm}
Each fiber is a smooth parallelizable manifold with boundary, having the homotopy type of a bouquet of  -spheres
-spheres 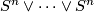 .
\end{thm}
.
\end{thm}
3 Invariants
Seen from the above section, the link  of an isolated singular point
of an isolated singular point  of a complex hypersurface
of a complex hypersurface  of complex dimension
of complex dimension  is a
is a  -connected
-connected 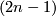 -dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a
-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a 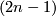 -dimensional closed manifold
-dimensional closed manifold  which is not a homotopy sphere,
which is not a homotopy sphere,  is the highest connectivity
is the highest connectivity  could have. Therefore to understand the classification and invariants of the links
could have. Therefore to understand the classification and invariants of the links  one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see highly-connected manifolds.
one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see highly-connected manifolds.
On the other hand, as the link  is closely related to the singular point
is closely related to the singular point  of the complex hypersurfaces, some of the topological invariants of
of the complex hypersurfaces, some of the topological invariants of  are computable from the polynomial.
are computable from the polynomial.
Let  be a complex hypersurface defined by
be a complex hypersurface defined by 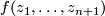 ,
,  be an isolated singular point of
be an isolated singular point of  . Let
. Let 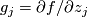
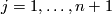 . By putting all these
. By putting all these 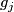 's together we get the gradient field of
's together we get the gradient field of  , which can be viewed as a map
, which can be viewed as a map 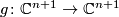 ,
, 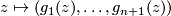 .
.
4 Classification
...
5 Further discussion
...
6 References
- [Milnor1968] J. Milnor, Singular points of complex hypersurfaces, Princeton University Press, Princeton, N.J., 1968. MR0239612 (39 #969) Zbl 0224.57014
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 .
.
2 Construction and examples
Let 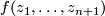 be a non-constant polynomial in
be a non-constant polynomial in 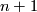 complex variables. A complex hypersurface
complex variables. A complex hypersurface  is the algebraic set consisting of points
is the algebraic set consisting of points 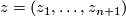 such that
such that 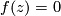 . A regular point
. A regular point 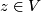 is a point at which some partial derivative
is a point at which some partial derivative 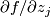 does not vanish; if at a point
does not vanish; if at a point 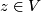 all the partial derivatives
all the partial derivatives 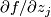 vanish,
vanish,  is called a singular point of
is called a singular point of  .
.
Near a regular point  , the complex hypersurface
, the complex hypersurface  is a smooth manifold of real dimension
is a smooth manifold of real dimension  ; in a small neighborhood of a singular point
; in a small neighborhood of a singular point  , the topology of the complex hypersurface
, the topology of the complex hypersurface  is more complicated. One way to look at the topology near
is more complicated. One way to look at the topology near  , due to Brauner, is to look at the intersection of
, due to Brauner, is to look at the intersection of  with a
with a 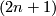 -dimensioanl sphere of small radius
-dimensioanl sphere of small radius 
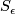 centered at
centered at  .
.
\begin{thm}
The space 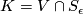 is
is  -connected.
\end{thm}
-connected.
\end{thm}
The topology of  is independent of the small paremeter
is independent of the small paremeter  , it is called the link of the singular point
, it is called the link of the singular point  .
.
\begin{thm}(Fibration Theorem)
For  sufficiently small, the space
sufficiently small, the space 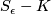 is a smooth fiber bundle over
is a smooth fiber bundle over  , with projection map
, with projection map 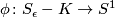 ,
, 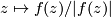 . Each fiber
. Each fiber 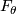 is parallelizable and has the homotopy type of a finite CW-complex of dimension
is parallelizable and has the homotopy type of a finite CW-complex of dimension  .
\end{thm}
.
\end{thm}
The fiber 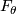 is usually called the Milnor fiber of the singular point
is usually called the Milnor fiber of the singular point  .
.
A singular point  is isolated if there is no other singular point in some small neighborhood of
is isolated if there is no other singular point in some small neighborhood of  .
.
In this special situation, the above theorems are strengthened to the following
\begin{thm}
Each fiber is a smooth parallelizable manifold with boundary, having the homotopy type of a bouquet of  -spheres
-spheres 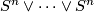 .
\end{thm}
.
\end{thm}
3 Invariants
Seen from the above section, the link  of an isolated singular point
of an isolated singular point  of a complex hypersurface
of a complex hypersurface  of complex dimension
of complex dimension  is a
is a  -connected
-connected 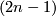 -dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a
-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a 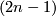 -dimensional closed manifold
-dimensional closed manifold  which is not a homotopy sphere,
which is not a homotopy sphere,  is the highest connectivity
is the highest connectivity  could have. Therefore to understand the classification and invariants of the links
could have. Therefore to understand the classification and invariants of the links  one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see highly-connected manifolds.
one needs to understand the classification and invariants of highly-connected odd dimensional manifolds, for which see highly-connected manifolds.
On the other hand, as the link  is closely related to the singular point
is closely related to the singular point  of the complex hypersurfaces, some of the topological invariants of
of the complex hypersurfaces, some of the topological invariants of  are computable from the polynomial.
are computable from the polynomial.
Let  be a complex hypersurface defined by
be a complex hypersurface defined by 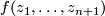 ,
,  be an isolated singular point of
be an isolated singular point of  . Let
. Let 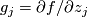
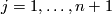 . By putting all these
. By putting all these 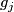 's together we get the gradient field of
's together we get the gradient field of  , which can be viewed as a map
, which can be viewed as a map 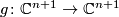 ,
, 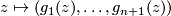 .
.
4 Classification
...
5 Further discussion
...
6 References
- [Milnor1968] J. Milnor, Singular points of complex hypersurfaces, Princeton University Press, Princeton, N.J., 1968. MR0239612 (39 #969) Zbl 0224.57014
|
This page has not been refereed. The information given here might be incomplete or provisional. |