Linking form
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Background: intersection forms
After Poincaré and Lefschetz, a closed oriented manifold 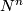 has a bilinear intersection form defined on its homology. Given a
has a bilinear intersection form defined on its homology. Given a 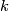 --chain
--chain 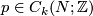 and an
and an 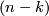 --chain
--chain 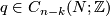 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 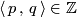 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
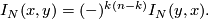
2 Definition of the linking form
 is the subgroup
is the subgroup 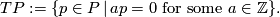
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 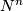 is the bilinear
is the bilinear 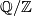 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
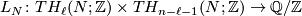
such that
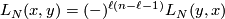
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 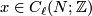 and
and 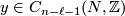 , let
, let 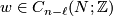 be such that
be such that 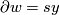 , for some
, for some 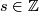 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 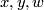 and
and  .
.
3 Definition via homology
Let 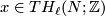 and let
and let 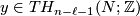 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
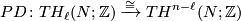
and
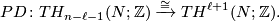
Associated to the short exact sequence of coefficients
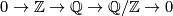
is the Bockstein long exact sequence in cohomology.
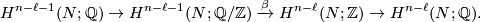
Choose 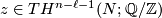 such that
such that 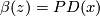 . This is always possible since torsion elements in
. This is always possible since torsion elements in 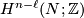 map to zero in
map to zero in 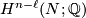 . There is a cup product:
. There is a cup product:
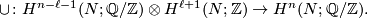
Compute 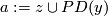 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
of  with the fundamental class of
with the fundamental class of  yields
yields 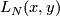 .
.
4 Example of 3-dimensional projective space
As an example, let 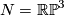 , so that
, so that 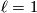 and
and  . Now
. Now 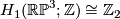 . Let
. Let 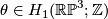 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 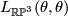 , consider
, consider 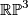 modelled as
modelled as 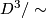 , with antipodal points on
, with antipodal points on 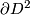 identified, and choose two representative
identified, and choose two representative  -chains
-chains  and
and  for
for 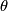 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 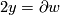 , where
, where 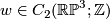 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 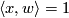 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 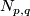 has
has 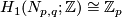 . The linking form is given on a generator
. The linking form is given on a generator 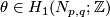 by
by 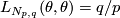 . Note that
. Note that 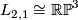 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 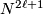
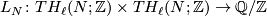
is an exact sequence:
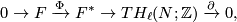
where  is a free abelain group and the linking
is a free abelain group and the linking 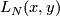 can be computed as follows. Let
can be computed as follows. Let 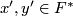 be such that
be such that 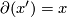 and
and 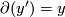 . Then we can tensor with
. Then we can tensor with 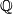 to obtain an isomorphism
to obtain an isomorphism
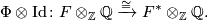
The linking form is given by:
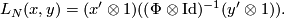
Let 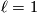 , so
, so 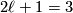 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. Let
is a rational homology 3-sphere. Let  be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for
be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 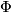 as above, which presents the linking form of
as above, which presents the linking form of  . The intersection form on a simply connected 4-manifold
. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~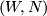 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
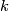 --chain
--chain 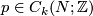 and an
and an 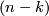 --chain
--chain 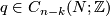 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 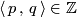 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
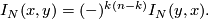
2 Definition of the linking form
 is the subgroup
is the subgroup 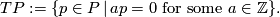
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 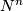 is the bilinear
is the bilinear 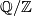 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
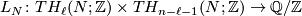
such that
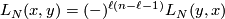
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 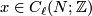 and
and 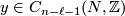 , let
, let 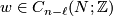 be such that
be such that 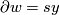 , for some
, for some 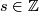 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 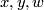 and
and  .
.
3 Definition via homology
Let 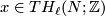 and let
and let 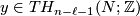 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
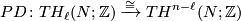
and
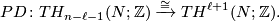
Associated to the short exact sequence of coefficients
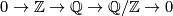
is the Bockstein long exact sequence in cohomology.
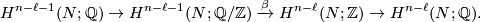
Choose 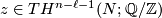 such that
such that 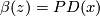 . This is always possible since torsion elements in
. This is always possible since torsion elements in 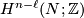 map to zero in
map to zero in 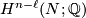 . There is a cup product:
. There is a cup product:
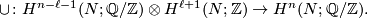
Compute 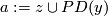 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
of  with the fundamental class of
with the fundamental class of  yields
yields 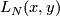 .
.
4 Example of 3-dimensional projective space
As an example, let 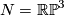 , so that
, so that 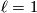 and
and  . Now
. Now 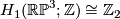 . Let
. Let 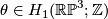 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 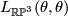 , consider
, consider 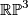 modelled as
modelled as 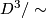 , with antipodal points on
, with antipodal points on 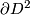 identified, and choose two representative
identified, and choose two representative  -chains
-chains  and
and  for
for 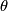 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 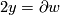 , where
, where 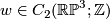 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 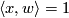 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 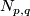 has
has 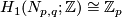 . The linking form is given on a generator
. The linking form is given on a generator 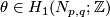 by
by 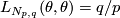 . Note that
. Note that 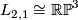 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 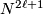
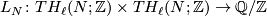
is an exact sequence:
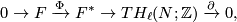
where  is a free abelain group and the linking
is a free abelain group and the linking 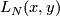 can be computed as follows. Let
can be computed as follows. Let 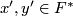 be such that
be such that 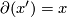 and
and 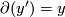 . Then we can tensor with
. Then we can tensor with 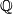 to obtain an isomorphism
to obtain an isomorphism
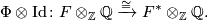
The linking form is given by:
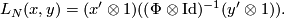
Let 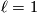 , so
, so 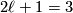 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. Let
is a rational homology 3-sphere. Let  be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for
be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 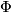 as above, which presents the linking form of
as above, which presents the linking form of  . The intersection form on a simply connected 4-manifold
. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~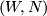 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
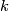 --chain
--chain 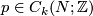 and an
and an 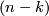 --chain
--chain 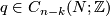 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 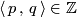 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
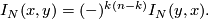
2 Definition of the linking form
 is the subgroup
is the subgroup 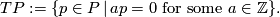
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 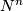 is the bilinear
is the bilinear 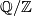 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
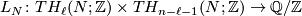
such that
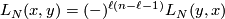
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 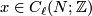 and
and 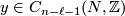 , let
, let 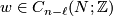 be such that
be such that 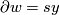 , for some
, for some 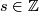 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 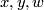 and
and  .
.
3 Definition via homology
Let 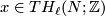 and let
and let 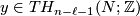 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
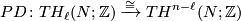
and
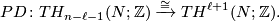
Associated to the short exact sequence of coefficients
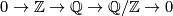
is the Bockstein long exact sequence in cohomology.
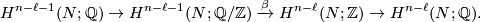
Choose 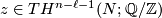 such that
such that 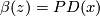 . This is always possible since torsion elements in
. This is always possible since torsion elements in 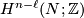 map to zero in
map to zero in 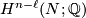 . There is a cup product:
. There is a cup product:
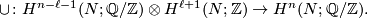
Compute 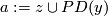 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
of  with the fundamental class of
with the fundamental class of  yields
yields 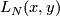 .
.
4 Example of 3-dimensional projective space
As an example, let 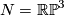 , so that
, so that 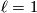 and
and  . Now
. Now 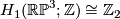 . Let
. Let 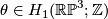 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 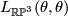 , consider
, consider 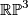 modelled as
modelled as 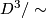 , with antipodal points on
, with antipodal points on 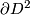 identified, and choose two representative
identified, and choose two representative  -chains
-chains  and
and  for
for 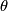 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 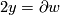 , where
, where 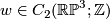 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 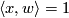 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 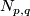 has
has 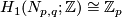 . The linking form is given on a generator
. The linking form is given on a generator 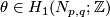 by
by 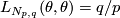 . Note that
. Note that 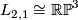 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 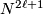
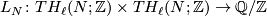
is an exact sequence:
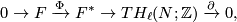
where  is a free abelain group and the linking
is a free abelain group and the linking 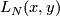 can be computed as follows. Let
can be computed as follows. Let 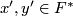 be such that
be such that 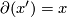 and
and 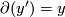 . Then we can tensor with
. Then we can tensor with 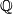 to obtain an isomorphism
to obtain an isomorphism
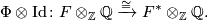
The linking form is given by:
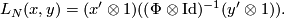
Let 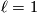 , so
, so 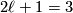 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. Let
is a rational homology 3-sphere. Let  be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for
be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 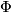 as above, which presents the linking form of
as above, which presents the linking form of  . The intersection form on a simply connected 4-manifold
. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~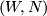 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401
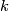 --chain
--chain 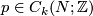 and an
and an 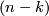 --chain
--chain 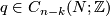 which is transverse to
which is transverse to  , the signed count of the intersections between
, the signed count of the intersections between  and
and  gives an intersection number
gives an intersection number 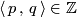 .
.
The intersection form is defined by
![\displaystyle I_N \colon H_k(N;\mathbb{Z}) \times H_{n-k}(N;\mathbb{Z}) \to \mathbb{Z}; ([p],[q]) \mapsto \langle p, q \rangle](/images/math/e/b/d/ebddd6200fa14a95e472da816b20076d.png)
and is such that
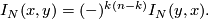
2 Definition of the linking form
 is the subgroup
is the subgroup 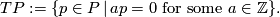
The analogue of the intersection pairing for the torsion part of the homology of a closed oriented manifold 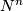 is the bilinear
is the bilinear 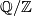 --valued linking form, which is due to Seifert [Seifert1933]:
--valued linking form, which is due to Seifert [Seifert1933]:
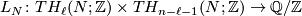
such that
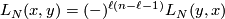
and computed as follows. Given ![[x] \in TH_\ell(N;\mathbb{Z})](/images/math/d/a/4/da4b6d59ddf4a9b94a1b58801617ff44.png) and
and ![[y] \in TH_{n-\ell-1}(N;\mathbb{Z})](/images/math/d/c/f/dcf6aac3ea142090318edf382dd35df1.png) represented by cycles
represented by cycles 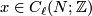 and
and 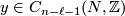 , let
, let 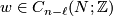 be such that
be such that 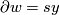 , for some
, for some 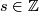 . Then we define:
. Then we define:
![\displaystyle L_N([x],[y]) := \langle x, w \rangle/s \in \mathbb{Q}/\mathbb{Z}.](/images/math/d/f/0/df0eb2fbf65c63b2e911c48228983104.png)
The resulting element is independent of the choices of 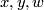 and
and  .
.
3 Definition via homology
Let 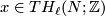 and let
and let 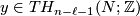 . Note that we have Poincaré duality isomorphisms
. Note that we have Poincaré duality isomorphisms
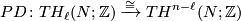
and
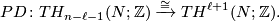
Associated to the short exact sequence of coefficients
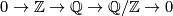
is the Bockstein long exact sequence in cohomology.
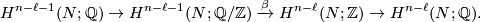
Choose 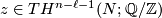 such that
such that 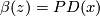 . This is always possible since torsion elements in
. This is always possible since torsion elements in 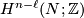 map to zero in
map to zero in 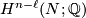 . There is a cup product:
. There is a cup product:
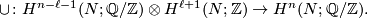
Compute 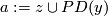 . Then the Kronecker pairing:
. Then the Kronecker pairing:
![\displaystyle \langle a,[N] \rangle \in \mathbb{Q}/\mathbb{Z}](/images/math/2/8/a/28a841ba31d7a473ec5cf00d1469d2ec.png)
of  with the fundamental class of
with the fundamental class of  yields
yields 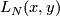 .
.
4 Example of 3-dimensional projective space
As an example, let 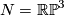 , so that
, so that 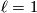 and
and  . Now
. Now 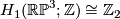 . Let
. Let 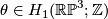 be the non-trivial element. To compute the linking
be the non-trivial element. To compute the linking 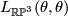 , consider
, consider 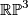 modelled as
modelled as 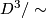 , with antipodal points on
, with antipodal points on 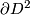 identified, and choose two representative
identified, and choose two representative  -chains
-chains  and
and  for
for 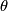 . Let
. Let  be the straight line between north and south poles and let
be the straight line between north and south poles and let  be half of the equator. Now
be half of the equator. Now 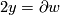 , where
, where 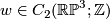 is the 2-disk whose boundary is the equator. We see that
is the 2-disk whose boundary is the equator. We see that 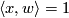 , so that
, so that
![\displaystyle L_{\mathbb{RP}^3}(\theta,\theta) = L_{\mathbb{RP}^3}([x],[y]) = \langle x,y \rangle/2 = 1/2.](/images/math/0/5/7/05725e0e70a522c8cbd35b7582e9aedd.png)
5 Example of lens spaces
Generalising the above example, the 3-dimensional lens space 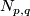 has
has 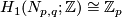 . The linking form is given on a generator
. The linking form is given on a generator 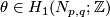 by
by 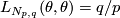 . Note that
. Note that 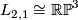 , so this is consistent with the above example.
, so this is consistent with the above example.
6 Presentations of linking forms
A presentation for a middle dimensional linking form on 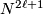
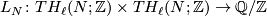
is an exact sequence:
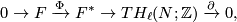
where  is a free abelain group and the linking
is a free abelain group and the linking 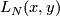 can be computed as follows. Let
can be computed as follows. Let 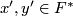 be such that
be such that 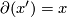 and
and 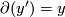 . Then we can tensor with
. Then we can tensor with 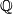 to obtain an isomorphism
to obtain an isomorphism
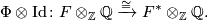
The linking form is given by:
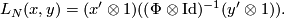
Let 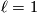 , so
, so 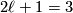 . Every 3-manifold
. Every 3-manifold  is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in
is the boundary of a simply connected 4-manifold, which is obtained by glueing 2-handles to an integrally framed link in  [Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for
[Lickorish1962], [Wallace1960]. This is sometimes called a surgery presentation for  . Suppose that
. Suppose that  is a rational homology 3-sphere. Let
is a rational homology 3-sphere. Let  be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for
be the matrix of (self-) linking numbers of the surgery presentation link. Taking the number of link components in the surgery presentation for  as the rank of
as the rank of  , the linking matrix
, the linking matrix  determines a map
determines a map 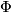 as above, which presents the linking form of
as above, which presents the linking form of  . The intersection form on a simply connected 4-manifold
. The intersection form on a simply connected 4-manifold  whose boundary is
whose boundary is  presents the linking form of
presents the linking form of  . This follows from the long exact sequence of the pair~
. This follows from the long exact sequence of the pair~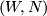 and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
and Poincar\'{e} duality. See [Boyer1986] for more details and the use of such presentations for the classification of simply connected 4-manifolds with a given boundary.
7 Classification of 5-manifolds
Linking forms are central to the classification of simply connected 5-manifolds. See this 5-manifolds page, which also describes the classification of anti-symmetric linking forms.
8 References
- [Boyer1986] S. Boyer, Simply-connected
 -manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
-manifolds with a given boundary, Trans. Amer. Math. Soc. 298 (1986), no.1, 331–357. MR857447 (88b:57023) Zbl 0790.57009
- [Lickorish1962] W. B. R. Lickorish, A representation of orientable combinatorial
 -manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
-manifolds, Ann. of Math. (2) 76 (1962), 531–540. MR0151948 (27 #1929) Zbl 0106.37102
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Wallace1960] A. H. Wallace, Modifications and cobounding manifolds, Canad. J. Math. 12 (1960), 503–528. MR0125588 (23 #A2887) Zbl 0116.40401