Laitinen conjecture
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Primary problem
Let  be a finite group. A real
be a finite group. A real  -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 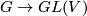 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 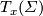 and
and 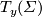 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 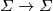 ,
, 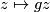 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 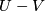 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 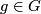 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 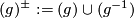 . Hereafter,
. Hereafter, 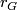 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 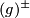 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 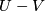 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 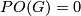 , if and only if
, if and only if  . In the case
. In the case 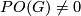 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 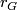 ,
, 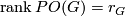 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 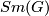 of
of  consisting of the differences
consisting of the differences 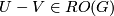 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 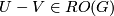 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 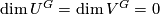 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 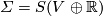 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 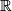 and diagonally on
and diagonally on 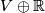 ). Therefore, the sets
). Therefore, the sets  and
and 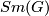 both contain the zero
both contain the zero 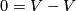 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 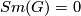 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 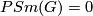 ?
?
Let 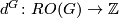 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 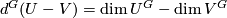 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
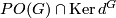 is trivial,
is trivial, 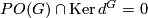 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 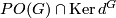 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 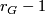 ,
, 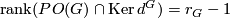 .
.
As 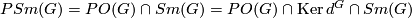 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 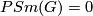 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 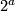 for
for 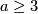 , the fixed point set
, the fixed point set 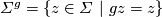 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 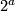 for
for 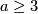 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 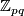 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 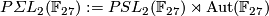 , the splitting extension of
, the splitting extension of 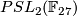 by the group
by the group 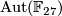 of automorphism of the field
of automorphism of the field 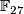 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
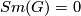 and
and  for
for 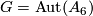 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 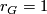 for
for 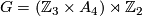 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 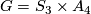 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 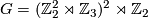 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 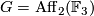 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 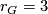 for
for 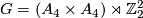 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
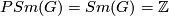 and
and 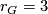 for
for 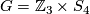 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
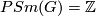 for
for 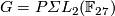 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 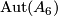 or
or 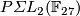 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 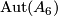 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
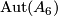 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
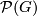 -matched
-matched 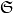 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 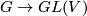 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 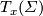 and
and 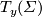 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 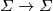 ,
, 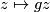 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 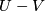 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 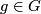 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 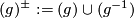 . Hereafter,
. Hereafter,  denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 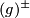 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences  of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 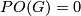 , if and only if
, if and only if  . In the case
. In the case 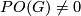 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 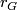 ,
, 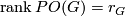 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 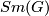 of
of  consisting of the differences
consisting of the differences 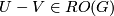 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 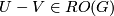 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 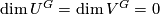 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 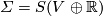 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 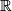 and diagonally on
and diagonally on 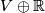 ). Therefore, the sets
). Therefore, the sets  and
and 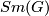 both contain the zero
both contain the zero 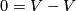 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 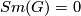 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 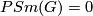 ?
?
Let 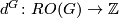 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 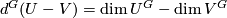 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
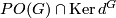 is trivial,
is trivial, 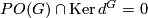 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 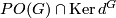 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 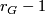 ,
, 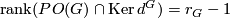 .
.
As 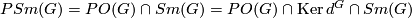 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 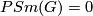 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 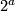 for
for 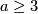 , the fixed point set
, the fixed point set 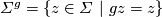 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 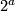 for
for 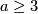 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 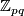 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 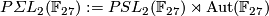 , the splitting extension of
, the splitting extension of 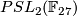 by the group
by the group 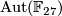 of automorphism of the field
of automorphism of the field 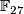 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
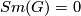 and
and  for
for 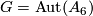 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 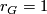 for
for 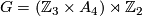 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 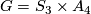 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 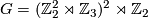 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 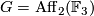 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 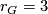 for
for 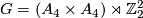 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
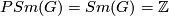 and
and 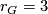 for
for 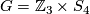 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
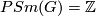 for
for 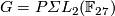 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 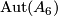 or
or 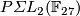 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 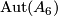 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
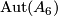 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
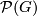 -matched
-matched  -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 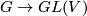 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 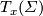 and
and 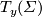 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 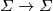 ,
, 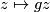 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 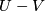 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 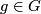 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 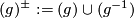 . Hereafter,
. Hereafter, 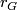 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 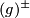 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 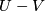 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 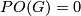 , if and only if
, if and only if  . In the case
. In the case 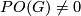 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 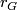 ,
, 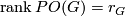 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 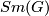 of
of  consisting of the differences
consisting of the differences 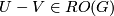 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 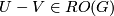 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 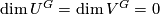 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 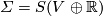 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 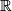 and diagonally on
and diagonally on 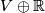 ). Therefore, the sets
). Therefore, the sets  and
and 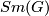 both contain the zero
both contain the zero 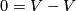 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 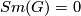 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 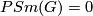 ?
?
Let 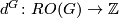 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 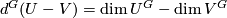 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
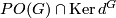 is trivial,
is trivial, 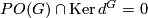 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 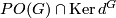 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 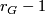 ,
, 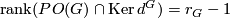 .
.
As 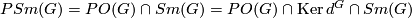 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 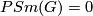 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 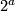 for
for 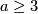 , the fixed point set
, the fixed point set 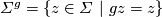 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 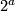 for
for 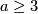 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 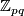 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 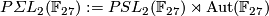 , the splitting extension of
, the splitting extension of 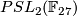 by the group
by the group 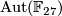 of automorphism of the field
of automorphism of the field 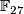 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
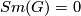 and
and  for
for 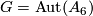 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 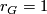 for
for 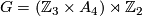 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 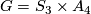 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 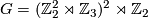 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 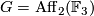 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 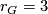 for
for 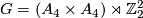 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
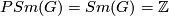 and
and 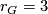 for
for 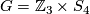 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
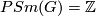 for
for 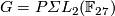 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 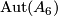 or
or 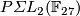 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 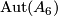 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
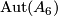 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
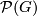 -matched
-matched 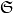 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 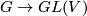 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 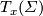 and
and 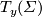 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 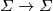 ,
, 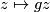 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 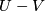 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 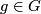 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 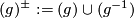 . Hereafter,
. Hereafter, 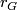 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 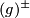 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 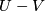 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 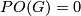 , if and only if
, if and only if  . In the case
. In the case 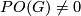 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 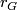 ,
, 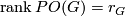 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 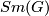 of
of  consisting of the differences
consisting of the differences 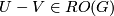 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 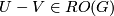 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 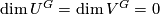 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 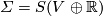 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 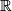 and diagonally on
and diagonally on 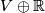 ). Therefore, the sets
). Therefore, the sets  and
and 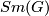 both contain the zero
both contain the zero 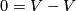 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 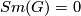 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 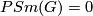 ?
?
Let 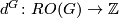 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 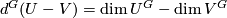 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
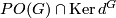 is trivial,
is trivial, 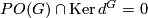 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 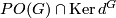 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 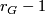 ,
, 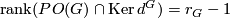 .
.
As 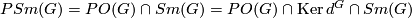 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 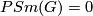 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 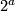 for
for 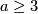 , the fixed point set
, the fixed point set 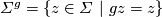 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 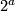 for
for 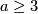 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 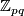 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 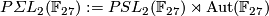 , the splitting extension of
, the splitting extension of 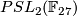 by the group
by the group 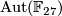 of automorphism of the field
of automorphism of the field 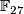 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
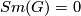 and
and  for
for 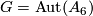 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 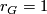 for
for 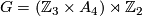 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 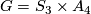 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 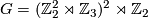 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 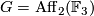 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 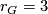 for
for 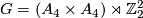 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
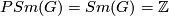 and
and 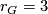 for
for 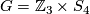 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
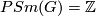 for
for 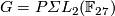 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 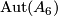 or
or 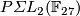 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 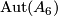 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
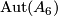 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
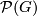 -matched
-matched 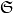 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 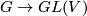 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 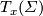 and
and 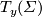 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 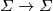 ,
, 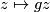 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 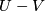 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 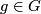 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 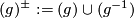 . Hereafter,
. Hereafter, 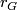 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 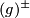 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 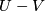 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 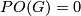 , if and only if
, if and only if  . In the case
. In the case 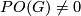 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 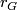 ,
, 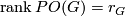 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 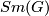 of
of  consisting of the differences
consisting of the differences 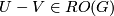 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 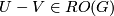 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 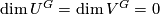 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 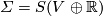 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 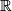 and diagonally on
and diagonally on 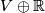 ). Therefore, the sets
). Therefore, the sets  and
and  both contain the zero
both contain the zero  of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 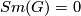 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 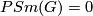 ?
?
Let 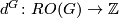 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 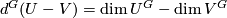 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
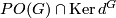 is trivial,
is trivial, 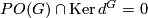 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 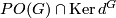 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 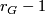 ,
, 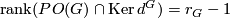 .
.
As 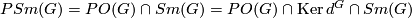 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 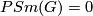 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 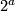 for
for 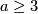 , the fixed point set
, the fixed point set 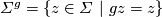 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 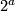 for
for 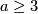 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 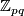 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 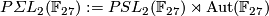 , the splitting extension of
, the splitting extension of 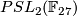 by the group
by the group 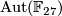 of automorphism of the field
of automorphism of the field 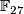 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
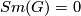 and
and  for
for 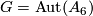 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 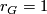 for
for 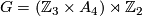 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 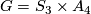 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 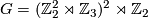 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 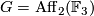 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 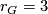 for
for 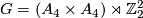 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
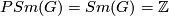 and
and 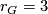 for
for 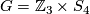 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
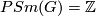 for
for 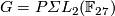 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 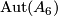 or
or 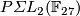 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 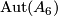 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
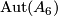 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
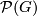 -matched
-matched 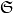 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 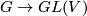 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 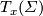 and
and 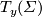 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 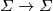 ,
, 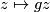 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 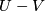 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 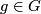 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 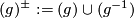 . Hereafter,
. Hereafter, 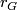 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 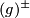 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences  of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 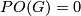 , if and only if
, if and only if  . In the case
. In the case 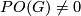 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 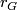 ,
, 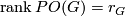 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 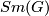 of
of  consisting of the differences
consisting of the differences 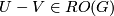 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 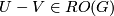 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 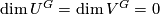 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 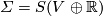 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 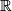 and diagonally on
and diagonally on 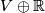 ). Therefore, the sets
). Therefore, the sets  and
and 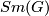 both contain the zero
both contain the zero 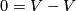 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 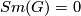 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 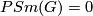 ?
?
Let 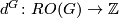 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 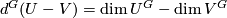 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
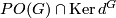 is trivial,
is trivial, 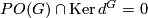 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 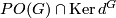 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 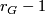 ,
, 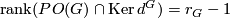 .
.
As 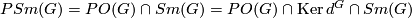 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 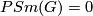 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 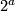 for
for 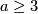 , the fixed point set
, the fixed point set 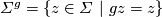 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 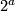 for
for 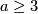 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to  for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to  , the splitting extension of
, the splitting extension of  by the group
by the group 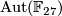 of automorphism of the field
of automorphism of the field 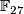 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
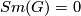 and
and  for
for 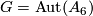 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 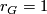 for
for 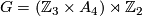 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 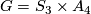 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 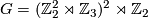 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 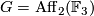 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 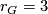 for
for 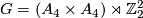 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
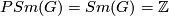 and
and 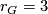 for
for 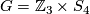 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
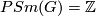 for
for 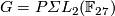 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 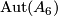 or
or 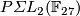 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to  , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
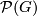 -matched
-matched 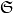 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 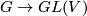 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 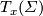 and
and 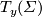 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 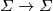 ,
, 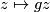 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 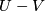 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 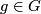 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 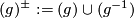 . Hereafter,
. Hereafter,  denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 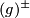 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 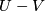 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 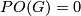 , if and only if
, if and only if  . In the case
. In the case 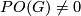 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 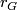 ,
, 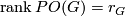 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 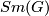 of
of  consisting of the differences
consisting of the differences 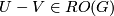 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 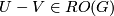 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 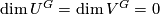 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 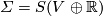 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on  and diagonally on
and diagonally on 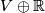 ). Therefore, the sets
). Therefore, the sets  and
and 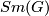 both contain the zero
both contain the zero 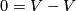 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 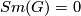 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 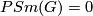 ?
?
Let 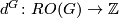 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 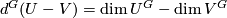 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
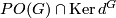 is trivial,
is trivial, 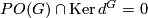 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 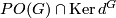 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 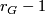 ,
, 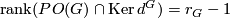 .
.
As 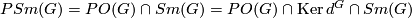 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 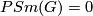 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 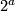 for
for 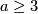 , the fixed point set
, the fixed point set 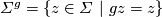 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 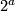 for
for 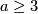 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 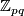 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 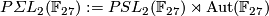 , the splitting extension of
, the splitting extension of 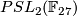 by the group
by the group 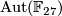 of automorphism of the field
of automorphism of the field 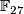 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
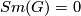 and
and  for
for 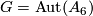 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 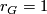 for
for 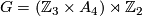 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 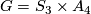 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 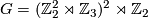 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 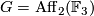 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 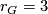 for
for 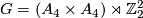 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
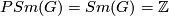 and
and  for
for 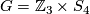 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
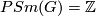 for
for 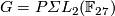 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 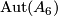 or
or 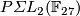 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to  , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
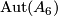 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
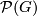 -matched
-matched  -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 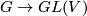 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 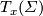 and
and 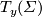 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 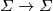 ,
, 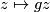 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 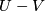 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 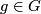 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 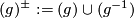 . Hereafter,
. Hereafter, 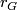 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 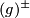 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 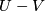 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 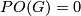 , if and only if
, if and only if  . In the case
. In the case 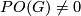 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 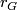 ,
, 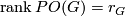 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset 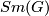 of
of  consisting of the differences
consisting of the differences 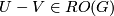 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 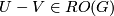 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 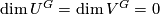 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere  admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on  and diagonally on
and diagonally on 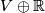 ). Therefore, the sets
). Therefore, the sets  and
and 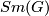 both contain the zero
both contain the zero 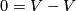 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 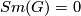 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 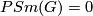 ?
?
Let 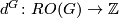 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 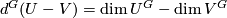 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
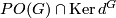 is trivial,
is trivial, 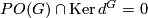 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 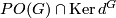 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 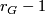 ,
, 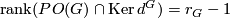 .
.
As 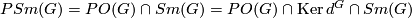 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 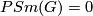 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 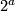 for
for 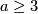 , the fixed point set
, the fixed point set 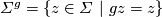 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order 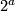 for
for 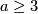 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 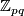 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 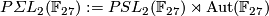 , the splitting extension of
, the splitting extension of 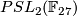 by the group
by the group 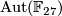 of automorphism of the field
of automorphism of the field 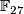 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
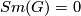 and
and  for
for 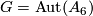 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 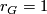 for
for 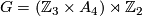 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 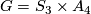 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 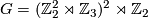 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 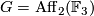 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 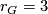 for
for 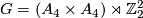 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
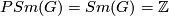 and
and  for
for 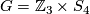 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
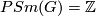 for
for 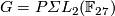 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 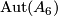 or
or 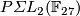 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 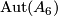 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
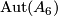 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
 -matched
-matched  -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501
 -module
-module  is a finite dimensional real vector space with a linear action of
is a finite dimensional real vector space with a linear action of  , i.e., the action of
, i.e., the action of  on
on  is given by a representation
is given by a representation 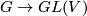 .
.
Definition 1.1. Two real  -modules
-modules  and
and  are called Smith equivalent if there exists a smooth action of
are called Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively, where the tangent
, respectively, where the tangent  -modules are determined on the tangent spaces
-modules are determined on the tangent spaces 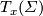 and
and 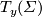 at
at  and
and  by taking the derivatives at
by taking the derivatives at  and
and  of the diffeomorphisms
of the diffeomorphisms 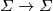 ,
, 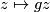 considered for all
considered for all  .
.
- Let
 be the representation ring of
be the representation ring of  , i.e., the Grothendieck ring of the differences
, i.e., the Grothendieck ring of the differences 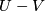 of real
of real  -modules
-modules  and
and  . As a group,
. As a group,  is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements
is a finitely generated free abelian group whose rank is the number of real conjugacy classes of elements 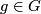 . Recall that the real conjugacy class of
. Recall that the real conjugacy class of  is defined by
is defined by 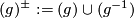 . Hereafter,
. Hereafter, 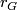 denotes the number of real conjugacy classes
denotes the number of real conjugacy classes 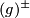 represented by elements
represented by elements  not of prime power order.
not of prime power order.
- Let
 be the subgroup of
be the subgroup of  consisting of the differences
consisting of the differences 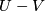 of two
of two  -matched real
-matched real  -modules
-modules  and
and  , where the
, where the  -matched condition means that
-matched condition means that  and
and  are isomorphic when restricted to any prime power order subgroup of
are isomorphic when restricted to any prime power order subgroup of  . The group
. The group  is trivial,
is trivial, 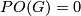 , if and only if
, if and only if  . In the case
. In the case 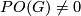 ,
,  is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 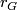 ,
, 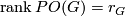 .
.
We shall make use of the notions of Smith set and pimary Smith set of  .
.
- The Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 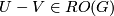 of two Smith equivalent real
of two Smith equivalent real  -modules
-modules  and
and  .
.
- The primary Smith set of
 is the subset
is the subset  of
of  consisting of the differences
consisting of the differences 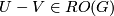 of two
of two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  .
.
If two real  -modules
-modules  and
and  with
with 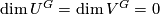 are isomorphic, then
are isomorphic, then  and
and  are Smith equivalent (the sphere
are Smith equivalent (the sphere 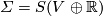 admits the required action of
admits the required action of  , where
, where  acts trivially on
acts trivially on 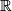 and diagonally on
and diagonally on 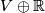 ). Therefore, the sets
). Therefore, the sets  and
and 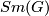 both contain the zero
both contain the zero 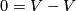 of
of  . The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
. The following problems are motivated by the question of Paul A. Smith posed in 1960, in the article [Smith1960, the footenote on p. 406].
- Is it true that any two Smith equivalent real
 -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 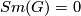 ?
?
- Is it true that any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e., is it true that
-modules are isomorphic, i.e., is it true that 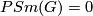 ?
?
Let 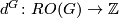 be the dimension homomorphism, i.e.,
be the dimension homomorphism, i.e., 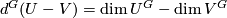 for any two real
for any two real  -modules
-modules  and
and  .
.
Lemma 1.2 (see [Laitinen&Pawałowski1999]). For a finite group  , the following two statements are true.
, the following two statements are true.
- The group
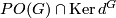 is trivial,
is trivial, 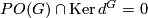 , if and only if
, if and only if  or
or  .
.
- If
 ,
, 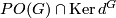 is a finitely generated free abelian group of rank
is a finitely generated free abelian group of rank 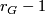 ,
, 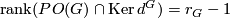 .
.
As 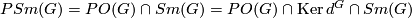 , Lemma 1.2 yields the following corollary.
, Lemma 1.2 yields the following corollary.
Corollary 1.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two
. Then any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic, i.e.,
-modules are isomorphic, i.e., 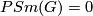 .
.
Problem 1.4 (Primary problem).
For which finite groups  , the following statement is true?
, the following statement is true?
- Any two
 -matched and Smith equivalent real
-matched and Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to answer the question in Problem 1.4, one shall check for which finite groups  with
with  , there exist two
, there exist two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real
-modules that are not isomorphic (cf. Corollary 1.3). For a systematic discussion on the Smith equivalence of real  -modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
-modules, we refer to the page Smith equivalence of reresentations. Here, we shall focus only on a related conjecture posed by Erkki Laitinen (cf. [Laitinen&Pawałowski1999, Appendix]).
[edit] 2 Laitinen conjecture
Definition 2.1.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are called Laitinen-Smith equivalent if there exists a smooth action of
are called Laitinen-Smith equivalent if there exists a smooth action of  on a homotopy sphere
on a homotopy sphere  with exactly two fixed points
with exactly two fixed points  and
and  at which the tangent
at which the tangent  -modules are isomorphic to
-modules are isomorphic to  and
and  , respectively (cf. Definition 1.1), and the action of
, respectively (cf. Definition 1.1), and the action of  on
on  satisfies the Laitinen condition asserting that for any element
satisfies the Laitinen condition asserting that for any element  of order
of order 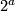 for
for 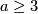 , the fixed point set
, the fixed point set 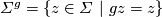 is connected.
is connected.
Definition 2.2.
Let  be a finite group. Two real
be a finite group. Two real  -modules
-modules  and
and  are said to be
are said to be  -matched if
-matched if  and
and  are isomorphic when restricted to any cyclic subgroup of
are isomorphic when restricted to any cyclic subgroup of  of order
of order  for
for 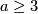 .
.
In Definition 2.1, the Laitinen condition implies that the two Smith equivalent real  -modules
-modules  and
and  are
are  -matched. As any two
-matched. As any two  -matched and Smith equivalent real
-matched and Smith equivalent real  -modules
-modules  and
and  are
are  -matched, Corollary 1.3 yields the next corollary.
-matched, Corollary 1.3 yields the next corollary.
Corollary 2.3.
Let  be a finite group with
be a finite group with  or
or  . Then any two Laitinen-Smith equivalent real
. Then any two Laitinen-Smith equivalent real  -modules are isomorphic.
-modules are isomorphic.
In 1996, Erkki Laitinen ([Laitinen&Pawałowski1999, Appendix]) posed the following conjecture (cf. Problem 1.4).
Problem 2.4 (Laitinen conjecture). For a finite Oliver group  , any two Laitinen-Smith equivalent real
, any two Laitinen-Smith equivalent real  -modules are isomorphic if and only if
-modules are isomorphic if and only if  or
or  .
.
In order to prove that the Laitinen conjecture holds for a finite Oliver group  , it sufficies to restrict attention to the case where
, it sufficies to restrict attention to the case where  , and to check that there exist two Laitinen-Smith equivalent real
, and to check that there exist two Laitinen-Smith equivalent real  -modules that are not isomorphic (cf. Corollary 2.3).
-modules that are not isomorphic (cf. Corollary 2.3).
[edit] 3 Results so far
- Laitinen and Pawałowski [Laitinen&Pawałowski1999] prove that the Laitinen conjecture holds for any finite (non-trivial) perfect group
 .
.
- Pawałowski and Solomon [Pawałowski&Solomon2002] prove that the Laitinen conjecture holds under either of the following condition:
-
 is a finite Oliver group of odd order (where always
is a finite Oliver group of odd order (where always  ).
).
-
 is a finite Oliver group with a quotient isomorphic to
is a finite Oliver group with a quotient isomorphic to 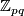 for two distinct odd primes
for two distinct odd primes  and
and  (where always
(where always  ).
).
-
 is a finite non-solvable gap group not isomorphic to
is a finite non-solvable gap group not isomorphic to 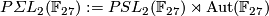 , the splitting extension of
, the splitting extension of 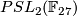 by the group
by the group 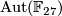 of automorphism of the field
of automorphism of the field 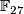 .
.
-
- Morimoto [Morimoto2008] obtains the first counterexample to the Laitinen conjecture by proving that the Smith set
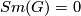 and
and  for
for 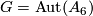 .
.
- Pawałowski and Sumi [Pawałowski&Sumi2009] compute the primary Smith set
 for some finite solvable Oliver groups, to the effect that:
for some finite solvable Oliver groups, to the effect that:
-
 and
and 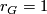 for
for 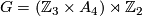 , confirming the Latinen conjecture.
, confirming the Latinen conjecture.
-
 and
and  for
for 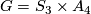 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 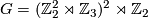 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and  for
for 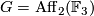 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
 and
and 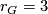 for
for 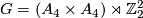 , contrary to the Laitinen conjecture.
, contrary to the Laitinen conjecture.
-
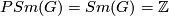 and
and 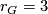 for
for 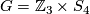 , and they prove that any element of
, and they prove that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
-
- Morimoto [Morimoto2010] checks that
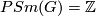 for
for 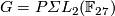 , where
, where  , and he proves that any element of
, and he proves that any element of  is the difference of two Laitinen-Smith equivalent real
is the difference of two Laitinen-Smith equivalent real  -modules, confirming the Laitinen conjecture.
-modules, confirming the Laitinen conjecture.
- Pawałowski and Sumi [Pawałowski&Sumi2010] confirm the Laitinen conjecture for any finite non-solvable group
 not isomorphic to
not isomorphic to 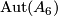 or
or 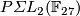 , and more generally, for any finite Oliver group
, and more generally, for any finite Oliver group  satisfying the Nil-Condition.
satisfying the Nil-Condition.
[edit] 4 Further discussion
Summarizing the results of [Laitinen&Pawałowski1999], [Pawałowski&Solomon2002], [Morimoto2008], [Morimoto2010], and [Pawałowski&Sumi2010], one obtains the following theorem.
Theorem 4.1. For a finite non-solvable group  not isomorphic to
not isomorphic to 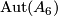 , the following two statements are true.
, the following two statements are true.
[edit] 5 References
- [Laitinen&Pawałowski1999] E. Laitinen and K. Pawałowski, Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), no.1, 297–307. MR1468195 (99b:57070) Zbl 0914.57025
- [Morimoto2008] M. Morimoto, Smith equivalent
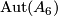 -representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
-representations are isomorphic, Proc. Amer. Math. Soc. 136 (2008), no.10, 3683–3688. MR2415055 (2009c:57054)
- [Morimoto2010] M. Morimoto, Nontrivial
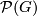 -matched
-matched 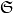 -related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
-related pairs for finite gap Oliver groups, J. Math. Soc. Japan 62 (2010), no.2, 623–647. MR2662855 ()
- [Pawałowski&Solomon2002] K. Pawałowski and R. Solomon, Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895 (electronic). MR1936973 (2003j:57057) Zbl 1022.57019
- [Pawałowski&Sumi2009] K. Pawałowski and T. Sumi, The Laitinen conjecture for finite solvable Oliver groups, Proc. Amer. Math. Soc. 137 (2009), no.6, 2147–2156. MR2480297 (2009k:57052) Zbl 1173.57015
- [Pawałowski&Sumi2010] K. Pawałowski and T. Sumi, Smith equivalence of representations and the Nil-Condition, to appear in the Proceedings of the Edinburgh Mathematical Society.
- [Smith1960] P. A. Smith, New results and old problems in finite transformation groups, Bull. Amer. Math. Soc. 66 (1960), 401–415. MR0125581 (23 #A2880) Zbl 0096.37501