Knotted tori

(Difference between revisions)

Jump to: navigation, search

Revision as of 12:48, 10 April 2010

Many interesting examples of embeddings are embeddings 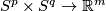$<wikitex> Many interesting examples of embeddings are embeddings $S^p\times S^q\to\Rr^m$, i.e. ''knotted tori''. See [[Embeddings just below the stable range: classification#Examples|Hudson tori]], \cite{Alexander1924}, \cite{Milgram&Rees1971}, \cite{Kosinski1961}, \cite{Hudson1963}, \cite{Wall1965}, \cite{Tindell1969}, \cite{Boechat&Haefliger1970}, \cite{Boechat1971}, \cite{Milgram&Rees1971}, \cite{Lucas&Saeki2002}, \cite{Skopenkov2002}. A classification of knotted tori is a natural next step (after the link theory \cite{Haefliger1966a}) and the [[Embeddings just below the stable range: classification#A generalization to highly-connected manifolds|classification of embeddings of highly-connected manifolds]]) towards classification of embeddings of ''arbitrary'' manifolds. Since the general [[High codimension embeddings: classification#Introduction|Knotting Problem]] is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori \cite{Skopenkov2006a}, \cite{Cencelj&Repov\v s&Skopenkov2007}, \cite{Cencelj&Repovš&Skopenkov2008} give some insight or even precise information concerning arbitrary manifolds (cf. \cite{Skopenkov2007}, \cite{Skopenkov2010}) and reveals new interesting relations to algebraic topology. For notation and conventions throughout this page see [[High_codimension_embeddings|high codimension embeddings]]. </wikitex> <wikitex> == Examples == One of the first examples were [[Embeddings just below the stable range: classification#Examples|Hudson tori]]. Let us construct a map $\tau:\pi_q(V_{m-q,p+1})\to E^m(S^p\times S^q)$. Recall that $\pi_q(V_{m-q,p+1})$ is isomorphic to the group of smooth maps $S^q\to V_{m-q,p+1}$ up to smooth homotopy. The latter maps can be considered as smooth maps $\varphi:S^q\times S^p\to\partial D^{m-q}$. Define the smooth embedding $\tau(\varphi)$ as the composition $$S^p\times S^q\overset{\varphi\times pr_2}\to\partial D^{m-q}\times S^q\subset D^{m-q}\times S^q\subset\Rr^m.$$ Here $pr_2$ is the projection onto the second factor and $\subset$ are the standard inclusions. </wikitex> == References == {{#RefList:}} [[Category:Manifolds]] [[Category:Embeddings of manifolds]] {{Stub}}S^p\times S^q\to\Rr^m$ , i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a]) and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repov\v s&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010]) and reveals new interesting relations to algebraic topology.

For notation and conventions throughout this page see high codimension embeddings.

Examples

One of the first examples were Hudson tori. Let us construct a map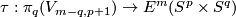 $\tau:\pi_q(V_{m-q,p+1})\to E^m(S^p\times S^q)$ $\tau:\pi_q(V_{m-q,p+1})\to E^m(S^p\times S^q)$ . Recall that 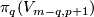$\pi_q(V_{m-q,p+1})$ $\pi_q(V_{m-q,p+1})$ is isomorphic to the group of smooth maps 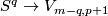$S^q\to V_{m-q,p+1}$ $S^q\to V_{m-q,p+1}$ up to smooth homotopy. The latter maps can be considered as smooth maps 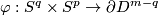$\varphi:S^q\times S^p\to\partial D^{m-q}$ $\varphi:S^q\times S^p\to\partial D^{m-q}$ . Define the smooth embedding 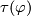$\tau(\varphi)$ $\tau(\varphi)$ as the composition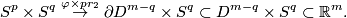

$\displaystyle S^p\times S^q\overset{\varphi\times pr_2}\to\partial D^{m-q}\times S^q\subset D^{m-q}\times S^q\subset\Rr^m.$ $\displaystyle S^p\times S^q\overset{\varphi\times pr_2}\to\partial D^{m-q}\times S^q\subset D^{m-q}\times S^q\subset\Rr^m.$

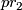Here $pr_2$ $pr_2$ is the projection onto the second factor and $\subset$ $\subset$ are the standard inclusions.

References

[Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
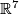[Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension $4$ dans $\Rr^7$ , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
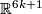[Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension $4k$ dans $\Rr^{6k+1}$ , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
[Cencelj&Repov\v s&Skopenkov2007] Template:Cencelj&Repov\v s&Skopenkov2007
[Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
[Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
[Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
[Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
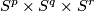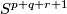[Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of $S^p\times S^q\times S^r$ in $S^{p+q+r+1}$ , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
[Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
[Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
[Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
[Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
[Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into 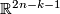$\Rr^{2n-k-1}$ , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
[Tindell1969] R. Tindell, Extending homeomorphisms of 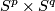$S\sp p \times S\sp q$ ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
[Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602

This page has not been refereed. The information given here might be incomplete or provisional.

Knotted tori

Revision as of 12:48, 10 April 2010

Examples

References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Interaction

Toolbox

@@ Line 1: / Line 1: @@
 <wikitex>
 Many interesting examples of embeddings are embeddings $S^p\times S^q\to\Rr^m$, i.e. ''knotted tori''. See [[Embeddings just below the stable range: classification#Examples|Hudson tori]], \cite{Alexander1924}, \cite{Milgram&Rees1971}, \cite{Kosinski1961}, \cite{Hudson1963}, \cite{Wall1965}, \cite{Tindell1969}, \cite{Boechat&Haefliger1970}, \cite{Boechat1971}, \cite{Milgram&Rees1971}, \cite{Lucas&Saeki2002}, \cite{Skopenkov2002}. A classification of knotted tori is a natural next step (after the link theory \cite{Haefliger1966a}) and the [[Embeddings just below the stable range: classification#A generalization to highly-connected manifolds|classification of embeddings of highly-connected manifolds]]) towards classification of embeddings of ''arbitrary'' manifolds. Since the general [[High codimension embeddings: classification#Introduction|Knotting Problem]] is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori \cite{Skopenkov2006a}, \cite{Cencelj&Repov\v s&Skopenkov2007}, \cite{Cencelj&Repovš&Skopenkov2008} give some insight or even precise information concerning arbitrary manifolds (cf. \cite{Skopenkov2007}, \cite{Skopenkov2010}) and reveals new interesting relations to algebraic topology.
-<!--For notation and conventions throughout this page see [[High_codimension_embeddings|high codimension embeddings]].-->
+For notation and conventions throughout this page see [[High_codimension_embeddings|high codimension embeddings]].
+</wikitex>
+<wikitex>
+== Examples ==
+One of the first examples were [[Embeddings just below the stable range: classification#Examples|Hudson tori]]. Let us construct a map $\tau:\pi_q(V_{m-q,p+1})\to E^m(S^p\times S^q)$. Recall that $\pi_q(V_{m-q,p+1})$ is isomorphic to the group of smooth maps $S^q\to V_{m-q,p+1}$ up to smooth homotopy. The latter maps can be considered as smooth maps $\varphi:S^q\times S^p\to\partial D^{m-q}$. Define the smooth embedding $\tau(\varphi)$ as the composition $$S^p\times S^q\overset{\varphi\times pr_2}\to\partial D^{m-q}\times S^q\subset D^{m-q}\times S^q\subset\Rr^m.$$ Here $pr_2$ is the projection onto the second factor and $\subset$ are the standard inclusions.
 </wikitex>