Knotted tori
Askopenkov (Talk | contribs) (→Classification) |
Askopenkov (Talk | contribs) (→Classification) |
||
| Line 102: | Line 102: | ||
For $m\ge2p+q+2$ we have $\pi_p(V_{m-p,q+1})=0$, so part (c) reduces to part (b) and the PL case of part (a). | For $m\ge2p+q+2$ we have $\pi_p(V_{m-p,q+1})=0$, so part (c) reduces to part (b) and the PL case of part (a). | ||
| − | {{beginthm|Theorem|\cite{Skopenkov2015a}}}\label{t:cornum} | + | {{beginthm|Theorem|\cite[Corollary 1.5.bd]{Skopenkov2015a}}}\label{t:cornum} |
Assume that $m\ge 2p+q+3$. | Assume that $m\ge 2p+q+3$. | ||
| − | (a) If $2m\ge p+3q+4$, then $ | + | (a) If $2m\ge p+3q+4$, then $KT^m_{p,q,\#}$ and $\pi_q(V_{m-q,p+1})$ have isomorphic subgroups with isomorphic quotients. |
| − | (b) If $2m\ge 3q+4$, then $ | + | (b) If $2m\ge 3q+4$, then $KT^m_{p,q,\#}$ has a subgroup isomorphic to $\pi_{p+2q+2-m}(V_{M+m-q-1,M})$ ($M$ large), |
whose quotient and $\pi_q(V_{m-q,p+1})$ have isomorphic subgroups with isomorphic quotients. | whose quotient and $\pi_q(V_{m-q,p+1})$ have isomorphic subgroups with isomorphic quotients. | ||
{{endthm}} | {{endthm}} | ||
| Line 116: | Line 116: | ||
$p$-framings' or `$D^p$-parametric connected sum'. Define $E^m_U(S^q\sqcup S^n) \subset E^m_D(S^q\sqcup S^n)$ to be the subgroup of links all whose components are unknotted. Let $\lambda=\lambda^m_{q,n}:E^m_D(S^q\sqcup S^n)\to\pi_q(S^{m-n-1})$ be the [[High_codimension_links#The_linking_coefficient|linking coefficient]]. Denote $K^m_{q,n}:=\ker\lambda\cap E^m_U(S^q\sqcup S^n)$. | $p$-framings' or `$D^p$-parametric connected sum'. Define $E^m_U(S^q\sqcup S^n) \subset E^m_D(S^q\sqcup S^n)$ to be the subgroup of links all whose components are unknotted. Let $\lambda=\lambda^m_{q,n}:E^m_D(S^q\sqcup S^n)\to\pi_q(S^{m-n-1})$ be the [[High_codimension_links#The_linking_coefficient|linking coefficient]]. Denote $K^m_{q,n}:=\ker\lambda\cap E^m_U(S^q\sqcup S^n)$. | ||
| − | {{beginthm|Conjecture}}\label{t:conj} | + | {{beginthm|Conjecture}}\label{t:conj} (a) If $2m\ge p+3q+4$, then $\tau\oplus_i\#:\pi_q(V_{m-q,p+1})\oplus E^m_D(S^{p+q})\to KT^m_{p,q,D}$ is an |
| − | For $m\ge2p+q+3$ | + | isomorphism. |
| + | |||
| + | (b) For $m\ge2p+q+3$ | ||
$$KT^m_{p,q}\cong E^m_D(D^{p+1}\times S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q}).$$ | $$KT^m_{p,q}\cong E^m_D(D^{p+1}\times S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q}).$$ | ||
{{endthm}} | {{endthm}} | ||
| Line 125: | Line 127: | ||
Denote by $TG$ the torsion subgroup of an abelian group $G$. | Denote by $TG$ the torsion subgroup of an abelian group $G$. | ||
| − | {{beginthm|Theorem|\cite[Corollary 1.7]{Skopenkov2015}, \cite{Skopenkov2015a}}}\label{t:cornum} | + | {{beginthm|Theorem|\cite[Corollary 1.7]{Skopenkov2015}, \cite[Corollary 1.4]{Skopenkov2015a}}}\label{t:cornum} |
Assume that $m\ge 2p+q+3$. | Assume that $m\ge 2p+q+3$. | ||
Revision as of 10:11, 12 April 2019
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Many interesting examples of embeddings are embeddings 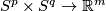 , i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a] and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008],
[Skopenkov2015], [Skopenkov2015a] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010], [Skopenkov2014]) and reveals new interesting relations to algebraic topology.
, i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a] and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008],
[Skopenkov2015], [Skopenkov2015a] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010], [Skopenkov2014]) and reveals new interesting relations to algebraic topology.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. We assume that
3]. We assume that 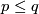 . Denote
. Denote
2 Examples
An 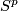 -parametric connected sum group structure on
-parametric connected sum group structure on 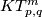 is constructed for
is constructed for  in [Skopenkov2006], [Skopenkov2015a].
in [Skopenkov2006], [Skopenkov2015a].
One of the first examples were Hudson tori.
Let us construct a map
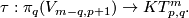
Recall that 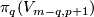 is isomorphic to the group of smooth maps
is isomorphic to the group of smooth maps 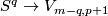 up to smooth homotopy. The latter maps can be considered as smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps 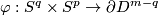 . Define the smooth embedding
. Define the smooth embedding 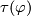 as the composition
as the composition
Tex syntax error
Tex syntax erroris the projection onto the second factor and
 is the standard inclusion.
is the standard inclusion.
Clearly,  is well-defined and, for
is well-defined and, for  , is a homomorphism.
, is a homomorphism.
Define the `embedded connected sum' or `local knotting' map
Tex syntax error
Tex syntax erroris well-defined and, for
 , is a homomorphism.
, is a homomorphism.
See construction of another map in [Skopenkov2015,  3, definition of
3, definition of 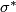 ].
].
3 Reduction to classification modulo knots
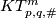 be the quotient set of
be the quotient set of 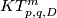 by the embedded connected sum action, i.e.
by the embedded connected sum action, i.e. Tex syntax error. Let
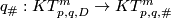 be the quotient map.
be the quotient map.
For  a group structure on
a group structure on 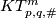 is well-defined by
is well-defined by 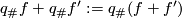 ,
, 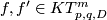 .
.
 the map
the map 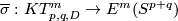 constructed by `embedded surgery of
constructed by `embedded surgery of 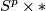 ' is well-defined [Skopenkov2015a,
' is well-defined [Skopenkov2015a,  3.3]. Clearly,
3.3]. Clearly, Tex syntax error.
The following result reduces description of 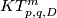 to description of
to description of 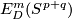 and of
and of
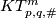 , cf. [Schmidt1971], [Crowley&Skopenkov2008, end of
, cf. [Schmidt1971], [Crowley&Skopenkov2008, end of  1].
1].
Lemma 3.1 [Skopenkov2015a, Smoothing Lemma 1.1].
For  the map
the map
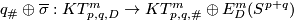
4 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that 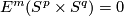 for
for 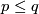 and
and 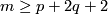 , provided that
, provided that 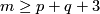 or
or 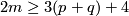 in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
We have the following table for 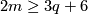 and for
and for 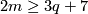 , for the PL and smooth categories, respectively.
, for the PL and smooth categories, respectively.
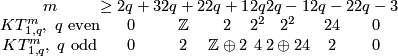
Here  is short for
is short for 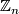 . The table follows from the theorems below.
. The table follows from the theorems below.
We also have 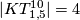 and
and 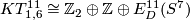 , of which
, of which 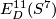 is rank one infinite [Skopenkov2015a].
is rank one infinite [Skopenkov2015a].
There is a finiteness criterion for 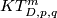 when
when  [Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
[Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
Theorem 4.1. There are isomorphisms, or, for 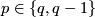 , 1-1 correspondences
, 1-1 correspondences
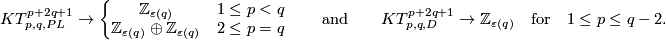
The isomorphisms and 1-1 correspondences are given by the Whitney invariant [Skopenkov2016e].
We have 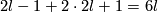 ; a description of
; a description of 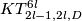 is given in [Skopenkov2016e, end of
is given in [Skopenkov2016e, end of  6.3].
6.3].
Theorem 4.1 can be generalized as follows.
Theorem 4.2. (a) If  and
and 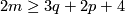 , then
, then
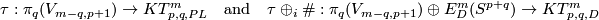
are isomorphisms.
(b) If 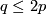 , then
, then
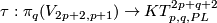
(c) If 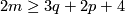 , then there is a 1-1 correspondence
, then there is a 1-1 correspondence
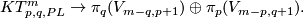
This follows for 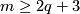 from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For  there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for
there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for 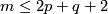 no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
For 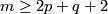 we have
we have 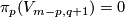 , so part (c) reduces to part (b) and the PL case of part (a).
, so part (c) reduces to part (b) and the PL case of part (a).
Theorem 4.3 [Skopenkov2015a, Corollary 1.5.bd].
Assume that 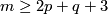 .
.
(a) If 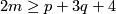 , then
, then 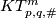 and
and 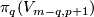 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
(b) If 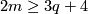 , then
, then 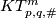 has a subgroup isomorphic to
has a subgroup isomorphic to 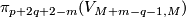 (
( large),
whose quotient and
large),
whose quotient and 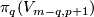 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
The following conjecture and results reduce description of 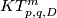 to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,
to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,  1.3] for methods of their calculations.
1.3] for methods of their calculations.
Abelian group structures on 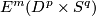 for
for  is defined analogously to the well-known case
is defined analogously to the well-known case 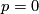 . The sum operation on
. The sum operation on 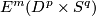 is `connected sum of
is `connected sum of  -spheres together with normal
-spheres together with normal
 -framings' or `
-framings' or `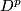 -parametric connected sum'. Define
-parametric connected sum'. Define 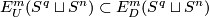 to be the subgroup of links all whose components are unknotted. Let
to be the subgroup of links all whose components are unknotted. Let 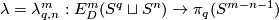 be the linking coefficient. Denote
be the linking coefficient. Denote 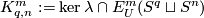 .
.
Conjecture 4.4. (a) If 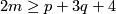 , then
, then 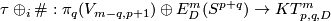 is an
isomorphism.
is an
isomorphism.
(b) For 
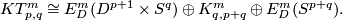
For a discussion see [Skopenkov2015a, Remark 1.9].
Denote by 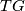 the torsion subgroup of an abelian group
the torsion subgroup of an abelian group  .
.
Theorem 4.5 [Skopenkov2015, Corollary 1.7], [Skopenkov2015a, Corollary 1.4].
Assume that 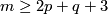 .
.
(a) ![KT^m_{D,p,q}\otimes\Q\cong[\pi_q(V_{m-q,p+1})\oplus E^m_D(S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q})]\otimes\Q](/images/math/e/8/c/e8ccc475e3ae649245d27594d1ffea82.png) .
.
(b) 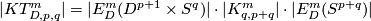 (more precisely, whenever one part is finite, the other is finite and they are equal).
(more precisely, whenever one part is finite, the other is finite and they are equal).
(c) 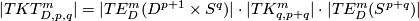 , unless
, unless 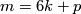 and
and 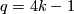 for some
for some  .
.
The above results were obtained using more `theoretical' results [Skopenkov2015, Theorem 1.6], [Skopenkov2015a, Theorem 1.2], see also [Cencelj&Repovš&Skopenkov2008, Theorem 2.1].
5 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans  , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 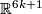 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
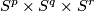 in
in 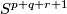 , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Schmidt1971] R. Schultz, On the inertia groups of a product of spheres, Trans. AMS, 156 (1971), 137–153.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
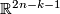 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
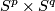 ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. We assume that
3]. We assume that 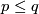 . Denote
. Denote
2 Examples
An 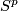 -parametric connected sum group structure on
-parametric connected sum group structure on 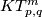 is constructed for
is constructed for  in [Skopenkov2006], [Skopenkov2015a].
in [Skopenkov2006], [Skopenkov2015a].
One of the first examples were Hudson tori.
Let us construct a map
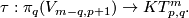
Recall that 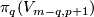 is isomorphic to the group of smooth maps
is isomorphic to the group of smooth maps 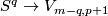 up to smooth homotopy. The latter maps can be considered as smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps 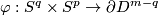 . Define the smooth embedding
. Define the smooth embedding 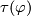 as the composition
as the composition
Tex syntax error
Tex syntax erroris the projection onto the second factor and
 is the standard inclusion.
is the standard inclusion.
Clearly,  is well-defined and, for
is well-defined and, for  , is a homomorphism.
, is a homomorphism.
Define the `embedded connected sum' or `local knotting' map
Tex syntax error
Tex syntax erroris well-defined and, for
 , is a homomorphism.
, is a homomorphism.
See construction of another map in [Skopenkov2015,  3, definition of
3, definition of 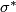 ].
].
3 Reduction to classification modulo knots
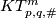 be the quotient set of
be the quotient set of 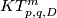 by the embedded connected sum action, i.e.
by the embedded connected sum action, i.e. Tex syntax error. Let
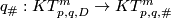 be the quotient map.
be the quotient map.
For  a group structure on
a group structure on 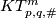 is well-defined by
is well-defined by 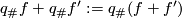 ,
, 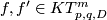 .
.
 the map
the map 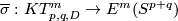 constructed by `embedded surgery of
constructed by `embedded surgery of 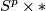 ' is well-defined [Skopenkov2015a,
' is well-defined [Skopenkov2015a,  3.3]. Clearly,
3.3]. Clearly, Tex syntax error.
The following result reduces description of 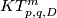 to description of
to description of 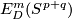 and of
and of
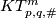 , cf. [Schmidt1971], [Crowley&Skopenkov2008, end of
, cf. [Schmidt1971], [Crowley&Skopenkov2008, end of  1].
1].
Lemma 3.1 [Skopenkov2015a, Smoothing Lemma 1.1].
For  the map
the map
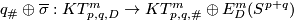
4 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that 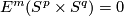 for
for 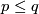 and
and 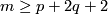 , provided that
, provided that 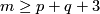 or
or 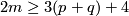 in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
We have the following table for 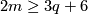 and for
and for 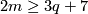 , for the PL and smooth categories, respectively.
, for the PL and smooth categories, respectively.
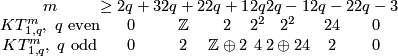
Here  is short for
is short for 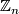 . The table follows from the theorems below.
. The table follows from the theorems below.
We also have 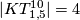 and
and 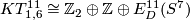 , of which
, of which 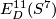 is rank one infinite [Skopenkov2015a].
is rank one infinite [Skopenkov2015a].
There is a finiteness criterion for 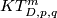 when
when  [Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
[Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
Theorem 4.1. There are isomorphisms, or, for 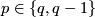 , 1-1 correspondences
, 1-1 correspondences
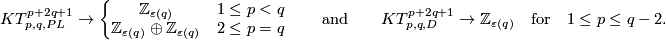
The isomorphisms and 1-1 correspondences are given by the Whitney invariant [Skopenkov2016e].
We have 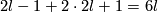 ; a description of
; a description of 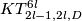 is given in [Skopenkov2016e, end of
is given in [Skopenkov2016e, end of  6.3].
6.3].
Theorem 4.1 can be generalized as follows.
Theorem 4.2. (a) If  and
and 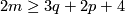 , then
, then
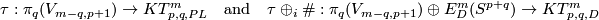
are isomorphisms.
(b) If 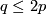 , then
, then
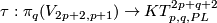
(c) If 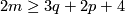 , then there is a 1-1 correspondence
, then there is a 1-1 correspondence
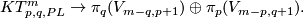
This follows for 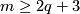 from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For  there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for
there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for 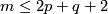 no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
For 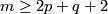 we have
we have 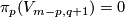 , so part (c) reduces to part (b) and the PL case of part (a).
, so part (c) reduces to part (b) and the PL case of part (a).
Theorem 4.3 [Skopenkov2015a, Corollary 1.5.bd].
Assume that 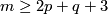 .
.
(a) If 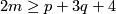 , then
, then 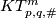 and
and 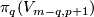 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
(b) If 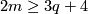 , then
, then 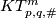 has a subgroup isomorphic to
has a subgroup isomorphic to 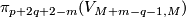 (
( large),
whose quotient and
large),
whose quotient and 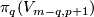 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
The following conjecture and results reduce description of 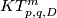 to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,
to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,  1.3] for methods of their calculations.
1.3] for methods of their calculations.
Abelian group structures on 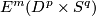 for
for  is defined analogously to the well-known case
is defined analogously to the well-known case 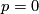 . The sum operation on
. The sum operation on 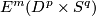 is `connected sum of
is `connected sum of  -spheres together with normal
-spheres together with normal
 -framings' or `
-framings' or `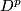 -parametric connected sum'. Define
-parametric connected sum'. Define 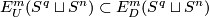 to be the subgroup of links all whose components are unknotted. Let
to be the subgroup of links all whose components are unknotted. Let 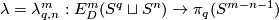 be the linking coefficient. Denote
be the linking coefficient. Denote 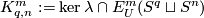 .
.
Conjecture 4.4. (a) If 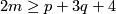 , then
, then 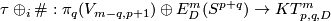 is an
isomorphism.
is an
isomorphism.
(b) For 
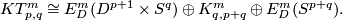
For a discussion see [Skopenkov2015a, Remark 1.9].
Denote by 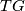 the torsion subgroup of an abelian group
the torsion subgroup of an abelian group  .
.
Theorem 4.5 [Skopenkov2015, Corollary 1.7], [Skopenkov2015a, Corollary 1.4].
Assume that 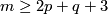 .
.
(a) ![KT^m_{D,p,q}\otimes\Q\cong[\pi_q(V_{m-q,p+1})\oplus E^m_D(S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q})]\otimes\Q](/images/math/e/8/c/e8ccc475e3ae649245d27594d1ffea82.png) .
.
(b) 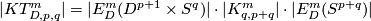 (more precisely, whenever one part is finite, the other is finite and they are equal).
(more precisely, whenever one part is finite, the other is finite and they are equal).
(c) 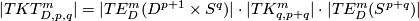 , unless
, unless 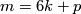 and
and 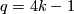 for some
for some  .
.
The above results were obtained using more `theoretical' results [Skopenkov2015, Theorem 1.6], [Skopenkov2015a, Theorem 1.2], see also [Cencelj&Repovš&Skopenkov2008, Theorem 2.1].
5 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans  , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 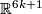 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
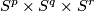 in
in 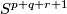 , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Schmidt1971] R. Schultz, On the inertia groups of a product of spheres, Trans. AMS, 156 (1971), 137–153.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
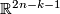 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
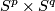 ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602
The isomorphisms and 1-1 correspondences are given by [[Embeddings_just_below_the_stable_range:_classification#The_Whitney_invariant|the Whitney invariant]] \cite{Skopenkov2016e}. We have l-1+2\cdot2l+1=6l$; a description of $KT^{6l}_{2l-1,2l,D}$ is given in \cite[end of $\S.3]{Skopenkov2016e}. Theorem \ref{kt1} can be generalized as follows. {{beginthm|Theorem}}\label{kt} (a) If $m\ge2p+q+3$ and m\ge3q+2p+4$, then $$\tau:\pi_q(V_{m-q,p+1})\to KT^m_{p,q,PL}\quad\text{and}\quad \tau\oplus_i\#:\pi_q(V_{m-q,p+1})\oplus E^m_D(S^{p+q})\to KT^m_{p,q,D}$$ are isomorphisms. (b) If $q\le2p$, then $$\tau:\pi_q(V_{2p+2,p+1})\to KT^{2p+q+2}_{p,q,PL}$$ is a 1-1 correspondence. (c) If m\ge3q+2p+4$, then there is a 1-1 correspondence $$KT^m_{p,q,PL}\to\pi_q(V_{m-q,p+1})\oplus\pi_p(V_{m-p,q+1}).$$ {{endthm}} This follows for $m\ge 2q+3$ from [[Embeddings_just_below_the_stable_range:_classification#Classification_further_below_the_stable_range|the Becker-Glover Theorem 5.3]]. For the general case see \cite[Corollary 1.5.a]{Skopenkov2002}. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For $m\ge2p+q+3$ there is an alternative direct proof of (a) \cite{Skopenkov2006}, \cite{Skopenkov2015a}, but for $m\le2p+q+2$ no proof of Theorem \ref{kt}.(b)(c) without referring to `the Haefliger-Wu invariant' is known. For $m\ge2p+q+2$ we have $\pi_p(V_{m-p,q+1})=0$, so part (c) reduces to part (b) and the PL case of part (a). {{beginthm|Theorem|\cite{Skopenkov2015a}}}\label{t:cornum} Assume that $m\ge 2p+q+3$. (a) If m\ge p+3q+4$, then $E^m_\#(S^p\times S^q)$ and $\pi_q(V_{m-q,p+1})$ have isomorphic subgroups with isomorphic quotients. (b) If m\ge 3q+4$, then $E^m_\#(S^p\times S^q)$ has a subgroup isomorphic to $\pi_{p+2q+2-m}(V_{M+m-q-1,M})$ ($M$ large), whose quotient and $\pi_q(V_{m-q,p+1})$ have isomorphic subgroups with isomorphic quotients. {{endthm}} The following conjecture and results reduce description of $KT^m_{p,q,D}$ to description of objects which are easier to calculate, at least in some cases, see \cite[$\SS^p\times S^q\to\Rr^m, i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a] and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008], [Skopenkov2015], [Skopenkov2015a] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010], [Skopenkov2014]) and reveals new interesting relations to algebraic topology.For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,
1,
3]. We assume that
. Denote
2 Examples
An
-parametric connected sum group structure on
is constructed for
in [Skopenkov2006], [Skopenkov2015a].
One of the first examples were Hudson tori.
Let us construct a map
Recall that
is isomorphic to the group of smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps
. Define the smooth embedding
as the composition
HereTex syntax errorTex syntax erroris the projection onto the second factor andis the standard inclusion.
Clearly,
is well-defined and, for
, is a homomorphism.
Define the `embedded connected sum' or `local knotting' map
Clearly,Tex syntax errorTex syntax erroris well-defined and, for, is a homomorphism.
See construction of another map in [Skopenkov2015,
3, definition of
].
3 Reduction to classification modulo knots
Let
be the quotient set of
by the embedded connected sum action, i.e.
Tex syntax error. Letbe the quotient map.
For
Fora group structure on
is well-defined by
,
.
the map
constructed by `embedded surgery of
' is well-defined [Skopenkov2015a,
3.3]. Clearly,
Tex syntax error.The following result reduces description of
to description of
and of
, cf. [Schmidt1971], [Crowley&Skopenkov2008, end of
1].
Lemma 3.1 [Skopenkov2015a, Smoothing Lemma 1.1]. For
the map
is an isomorphism.4 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that
for
and
, provided that
or
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
We have the following table for
and for
, for the PL and smooth categories, respectively.
Here
is short for
. The table follows from the theorems below.
We also have
and
, of which
is rank one infinite [Skopenkov2015a].
There is a finiteness criterion for
when
[Skopenkov2015, Theorem 1.4]. The formulation is not so short but effective. This criterion is a corollary of Theorem 4.5 below.
Theorem 4.1. There are isomorphisms, or, for
, 1-1 correspondences
The isomorphisms and 1-1 correspondences are given by the Whitney invariant [Skopenkov2016e].
We have
; a description of
is given in [Skopenkov2016e, end of
6.3].
Theorem 4.1 can be generalized as follows.
Theorem 4.2. (a) If
and
, then
are isomorphisms.
(b) If
, then
is a 1-1 correspondence.(c) If
, then there is a 1-1 correspondence
This follows for
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For
there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for
no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
For
we have
, so part (c) reduces to part (b) and the PL case of part (a).
Theorem 4.3 [Skopenkov2015a, Corollary 1.5.bd]. Assume that
.
(a) If
, then
and
have isomorphic subgroups with isomorphic quotients.
(b) If
, then
has a subgroup isomorphic to
(
large), whose quotient and
have isomorphic subgroups with isomorphic quotients.
The following conjecture and results reduce description of
to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,
1.3] for methods of their calculations.
Abelian group structures on
for
is defined analogously to the well-known case
. The sum operation on
is `connected sum of
-spheres together with normal
-framings' or `
-parametric connected sum'. Define
to be the subgroup of links all whose components are unknotted. Let
be the linking coefficient. Denote
.
Conjecture 4.4. (a) If
, then
is an isomorphism.
(b) For

For a discussion see [Skopenkov2015a, Remark 1.9].
Denote by
the torsion subgroup of an abelian group
.
Theorem 4.5 [Skopenkov2015, Corollary 1.7], [Skopenkov2015a, Corollary 1.4]. Assume that
.
(a)
.
(b)
(more precisely, whenever one part is finite, the other is finite and they are equal).
(c)
, unless
and
for some
.
The above results were obtained using more `theoretical' results [Skopenkov2015, Theorem 1.6], [Skopenkov2015a, Theorem 1.2], see also [Cencelj&Repovš&Skopenkov2008, Theorem 2.1].
5 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
dans
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
dans
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
in
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Schmidt1971] R. Schultz, On the inertia groups of a product of spheres, Trans. AMS, 156 (1971), 137–153.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
.3]{Skopenkov2015a} for methods of their calculations. Abelian group structures on $E^m(D^p\times S^q)$ for $m\ge q+3$ is defined analogously to the well-known case $p=0$. The sum operation on $E^m(D^p\times S^q)$ is `connected sum of $q$-spheres together with normal $p$-framings' or `$D^p$-parametric connected sum'. Define $E^m_U(S^q\sqcup S^n) \subset E^m_D(S^q\sqcup S^n)$ to be the subgroup of links all whose components are unknotted. Let $\lambda=\lambda^m_{q,n}:E^m_D(S^q\sqcup S^n)\to\pi_q(S^{m-n-1})$ be the [[High_codimension_links#The_linking_coefficient|linking coefficient]]. Denote $K^m_{q,n}:=\ker\lambda\cap E^m_U(S^q\sqcup S^n)$. {{beginthm|Conjecture}}\label{t:conj} For $m\ge2p+q+3$ $$KT^m_{p,q}\cong E^m_D(D^{p+1}\times S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q}).$$ {{endthm}} For a discussion see \cite[Remark 1.9]{Skopenkov2015a}. Denote by $TG$ the torsion subgroup of an abelian group $G$. {{beginthm|Theorem|\cite[Corollary 1.7]{Skopenkov2015}, \cite{Skopenkov2015a}}}\label{t:cornum} Assume that $m\ge 2p+q+3$. (a) $KT^m_{D,p,q}\otimes\Q\cong[\pi_q(V_{m-q,p+1})\oplus E^m_D(S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q})]\otimes\Q$. (b) $|KT^m_{D,p,q}|=|E^m_D(D^{p+1}\times S^q)|\cdot|K^m_{q,p+q}|\cdot|E^m_D(S^{p+q})|$ (more precisely, whenever one part is finite, the other is finite and they are equal). (c) $|TKT^m_{D,p,q}|=|TE^m_D(D^{p+1}\times S^q)|\cdot|TK^m_{q,p+q}|\cdot|TE^m_D(S^{p+q})|$, unless $m=6k+p$ and $q=4k-1$ for some $k$. {{endthm}} The above results were obtained using more `theoretical' results \cite[Theorem 1.6]{Skopenkov2015}, \cite[Theorem 1.2]{Skopenkov2015a}, see also \cite[Theorem 2.1]{Cencelj&Repovš&Skopenkov2008}.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. We assume that
3]. We assume that 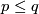 . Denote
. Denote
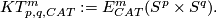
2 Examples
An 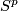 -parametric connected sum group structure on
-parametric connected sum group structure on 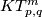 is constructed for
is constructed for  in [Skopenkov2006], [Skopenkov2015a].
in [Skopenkov2006], [Skopenkov2015a].
One of the first examples were Hudson tori.
Let us construct a map
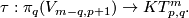
Recall that 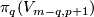 is isomorphic to the group of smooth maps
is isomorphic to the group of smooth maps 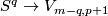 up to smooth homotopy. The latter maps can be considered as smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps 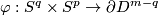 . Define the smooth embedding
. Define the smooth embedding 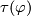 as the composition
as the composition
Tex syntax error
Tex syntax erroris the projection onto the second factor and
 is the standard inclusion.
is the standard inclusion.
Clearly,  is well-defined and, for
is well-defined and, for  , is a homomorphism.
, is a homomorphism.
Define the `embedded connected sum' or `local knotting' map
Tex syntax error
Tex syntax erroris well-defined and, for
 , is a homomorphism.
, is a homomorphism.
See construction of another map in [Skopenkov2015,  3, definition of
3, definition of 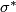 ].
].
3 Reduction to classification modulo knots
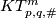 be the quotient set of
be the quotient set of 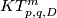 by the embedded connected sum action, i.e.
by the embedded connected sum action, i.e. Tex syntax error. Let
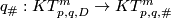 be the quotient map.
be the quotient map.
For  a group structure on
a group structure on 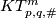 is well-defined by
is well-defined by 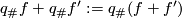 ,
, 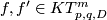 .
.
 the map
the map 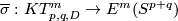 constructed by `embedded surgery of
constructed by `embedded surgery of 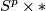 ' is well-defined [Skopenkov2015a,
' is well-defined [Skopenkov2015a,  3.3]. Clearly,
3.3]. Clearly, Tex syntax error.
The following result reduces description of 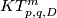 to description of
to description of 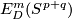 and of
and of
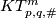 , cf. [Schmidt1971], [Crowley&Skopenkov2008, end of
, cf. [Schmidt1971], [Crowley&Skopenkov2008, end of  1].
1].
Lemma 3.1 [Skopenkov2015a, Smoothing Lemma 1.1].
For  the map
the map
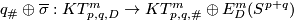
4 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that 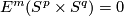 for
for 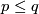 and
and 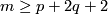 , provided that
, provided that 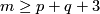 or
or 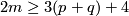 in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
We have the following table for 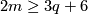 and for
and for 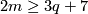 , for the PL and smooth categories, respectively.
, for the PL and smooth categories, respectively.
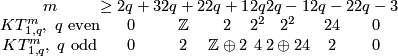
Here  is short for
is short for 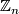 . The table follows from the theorems below.
. The table follows from the theorems below.
We also have 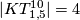 and
and 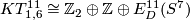 , of which
, of which 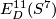 is rank one infinite [Skopenkov2015a].
is rank one infinite [Skopenkov2015a].
There is a finiteness criterion for 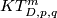 when
when  [Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
[Skopenkov2015, Theorem 1.4].
The formulation is not so short but effective.
This criterion is a corollary of Theorem 4.5 below.
Theorem 4.1. There are isomorphisms, or, for 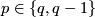 , 1-1 correspondences
, 1-1 correspondences
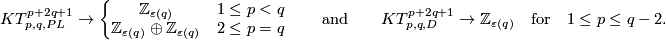
The isomorphisms and 1-1 correspondences are given by the Whitney invariant [Skopenkov2016e].
We have 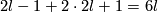 ; a description of
; a description of 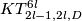 is given in [Skopenkov2016e, end of
is given in [Skopenkov2016e, end of  6.3].
6.3].
Theorem 4.1 can be generalized as follows.
Theorem 4.2. (a) If  and
and 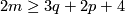 , then
, then
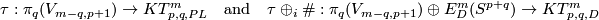
are isomorphisms.
(b) If 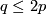 , then
, then
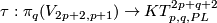
(c) If 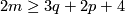 , then there is a 1-1 correspondence
, then there is a 1-1 correspondence
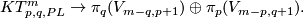
This follows for 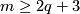 from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving configuration space of distinct pairs. For  there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for
there is an alternative direct proof of (a) [Skopenkov2006], [Skopenkov2015a], but for 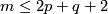 no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
no proof of Theorem 4.2.(b)(c) without referring to `the Haefliger-Wu invariant' is known.
For 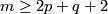 we have
we have 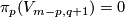 , so part (c) reduces to part (b) and the PL case of part (a).
, so part (c) reduces to part (b) and the PL case of part (a).
Theorem 4.3 [Skopenkov2015a, Corollary 1.5.bd].
Assume that 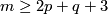 .
.
(a) If 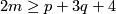 , then
, then 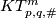 and
and 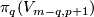 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
(b) If 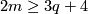 , then
, then 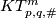 has a subgroup isomorphic to
has a subgroup isomorphic to 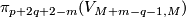 (
( large),
whose quotient and
large),
whose quotient and 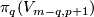 have isomorphic subgroups with isomorphic quotients.
have isomorphic subgroups with isomorphic quotients.
The following conjecture and results reduce description of 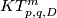 to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,
to description of objects which are easier to calculate, at least in some cases, see [Skopenkov2015a,  1.3] for methods of their calculations.
1.3] for methods of their calculations.
Abelian group structures on 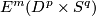 for
for  is defined analogously to the well-known case
is defined analogously to the well-known case 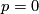 . The sum operation on
. The sum operation on 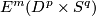 is `connected sum of
is `connected sum of  -spheres together with normal
-spheres together with normal
 -framings' or `
-framings' or `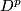 -parametric connected sum'. Define
-parametric connected sum'. Define 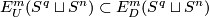 to be the subgroup of links all whose components are unknotted. Let
to be the subgroup of links all whose components are unknotted. Let 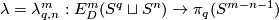 be the linking coefficient. Denote
be the linking coefficient. Denote 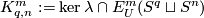 .
.
Conjecture 4.4. (a) If 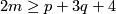 , then
, then 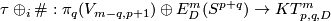 is an
isomorphism.
is an
isomorphism.
(b) For 
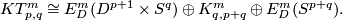
For a discussion see [Skopenkov2015a, Remark 1.9].
Denote by 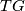 the torsion subgroup of an abelian group
the torsion subgroup of an abelian group  .
.
Theorem 4.5 [Skopenkov2015, Corollary 1.7], [Skopenkov2015a, Corollary 1.4].
Assume that 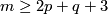 .
.
(a) ![KT^m_{D,p,q}\otimes\Q\cong[\pi_q(V_{m-q,p+1})\oplus E^m_D(S^q)\oplus K^m_{q,p+q}\oplus E^m_D(S^{p+q})]\otimes\Q](/images/math/e/8/c/e8ccc475e3ae649245d27594d1ffea82.png) .
.
(b) 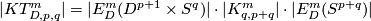 (more precisely, whenever one part is finite, the other is finite and they are equal).
(more precisely, whenever one part is finite, the other is finite and they are equal).
(c) 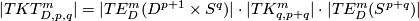 , unless
, unless 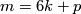 and
and 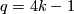 for some
for some  .
.
The above results were obtained using more `theoretical' results [Skopenkov2015, Theorem 1.6], [Skopenkov2015a, Theorem 1.2], see also [Cencelj&Repovš&Skopenkov2008, Theorem 2.1].
5 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans  , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 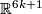 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
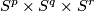 in
in 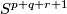 , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Schmidt1971] R. Schultz, On the inertia groups of a product of spheres, Trans. AMS, 156 (1971), 137–153.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
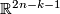 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
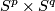 ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602