Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for  one constructs a smooth embedding
one constructs a smooth embedding 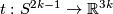 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even this embedding is a generator of
even this embedding is a generator of 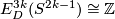 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 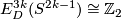 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for  .
.
3 Classification
Theorem 3.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 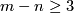 the group
the group  is finite unless
is finite unless 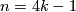 and
and 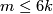 , when
, when  is the sum of
is the sum of 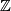 and a finite group.
and a finite group.
Theorem 3.2 (Haefliger-Milgram).
We have the following table for the group  ; in the table
; in the table 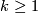 :
:
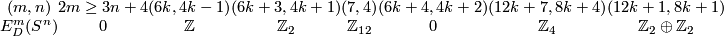
Proof for the first four columns, and for the fifth column,  even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,
even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case
3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case 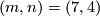 are given in [Skopenkov2005], [Crowley&Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008].
Theorem 3.3 [Milgram1972, Corollary G].
We have 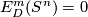 if and only if either
if and only if either 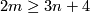 , or
, or 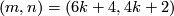 , or
, or 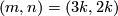 and
and 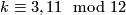 , or
, or 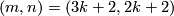 and
and 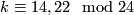 .
.
For a description of 2-components of  see [Milgram1972, Theorem F].
see [Milgram1972, Theorem F].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 3.4 [Haefliger1966].
For 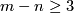 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
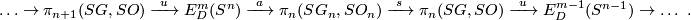
Here 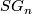 be the space of maps
be the space of maps 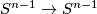 of degree
of degree  .
Restricting an element of
.
Restricting an element of 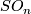 to
to 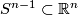 identifies
identifies 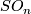 as a subspace of
as a subspace of 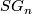 .
Let
.
Let 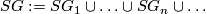 . Analogously define
. Analogously define 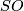 . Let
. Let  be the stabilization homomorphism.
The attaching invariant
be the stabilization homomorphism.
The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 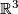 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
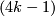 -spheres in
-spheres in 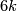 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
 3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for  one constructs a smooth embedding
one constructs a smooth embedding 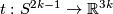 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even this embedding is a generator of
even this embedding is a generator of 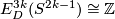 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 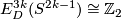 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 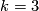 .
.
3 Classification
Theorem 3.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 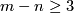 the group
the group  is finite unless
is finite unless 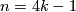 and
and 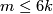 , when
, when  is the sum of
is the sum of 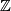 and a finite group.
and a finite group.
Theorem 3.2 (Haefliger-Milgram).
We have the following table for the group  ; in the table
; in the table 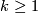 :
:
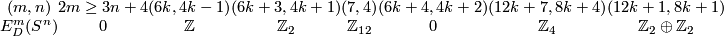
Proof for the first four columns, and for the fifth column,  even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,
even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case
3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case 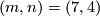 are given in [Skopenkov2005], [Crowley&Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008].
Theorem 3.3 [Milgram1972, Corollary G].
We have 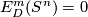 if and only if either
if and only if either 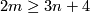 , or
, or 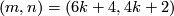 , or
, or 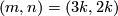 and
and 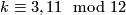 , or
, or 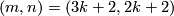 and
and 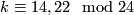 .
.
For a description of 2-components of  see [Milgram1972, Theorem F].
see [Milgram1972, Theorem F].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 3.4 [Haefliger1966].
For 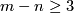 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
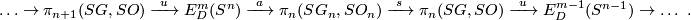
Here 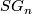 be the space of maps
be the space of maps 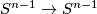 of degree
of degree  .
Restricting an element of
.
Restricting an element of 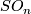 to
to 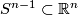 identifies
identifies 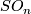 as a subspace of
as a subspace of 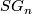 .
Let
.
Let 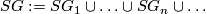 . Analogously define
. Analogously define 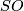 . Let
. Let  be the stabilization homomorphism.
The attaching invariant
be the stabilization homomorphism.
The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 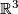 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
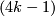 -spheres in
-spheres in 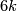 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
 3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for  one constructs a smooth embedding
one constructs a smooth embedding 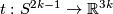 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even this embedding is a generator of
even this embedding is a generator of 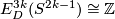 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 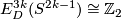 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 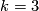 .
.
3 Classification
Theorem 3.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 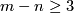 the group
the group  is finite unless
is finite unless 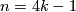 and
and 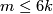 , when
, when  is the sum of
is the sum of 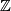 and a finite group.
and a finite group.
Theorem 3.2 (Haefliger-Milgram).
We have the following table for the group  ; in the table
; in the table 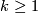 :
:
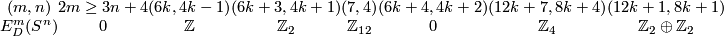
Proof for the first four columns, and for the fifth column,  even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,
even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case
3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case 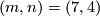 are given in [Skopenkov2005], [Crowley&Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008].
Theorem 3.3 [Milgram1972, Corollary G].
We have 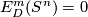 if and only if either
if and only if either 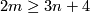 , or
, or 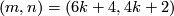 , or
, or 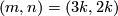 and
and 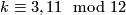 , or
, or 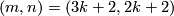 and
and 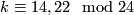 .
.
For a description of 2-components of  see [Milgram1972, Theorem F].
see [Milgram1972, Theorem F].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 3.4 [Haefliger1966].
For 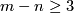 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
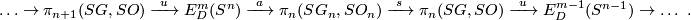
Here 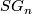 be the space of maps
be the space of maps 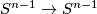 of degree
of degree  .
Restricting an element of
.
Restricting an element of 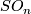 to
to 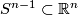 identifies
identifies 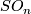 as a subspace of
as a subspace of 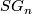 .
Let
.
Let 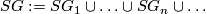 . Analogously define
. Analogously define 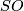 . Let
. Let  be the stabilization homomorphism.
The attaching invariant
be the stabilization homomorphism.
The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 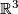 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
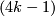 -spheres in
-spheres in 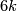 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.