Intersection number of immersions
Askopenkov (Talk | contribs) |
Askopenkov (Talk | contribs) (→Statement) |
||
| Line 30: | Line 30: | ||
{{endthm}} | {{endthm}} | ||
| − | This clasical fact is either a theorem or a definition depending on which definition of homology intersection pairing one accepts. For a proof see \cite{Scorpan2005|Section 3.2} or \cite{Ranicki2002|Proposition 7.22}. Unless this equality is a definition, the left- and right- hand sides of the equality can be called ''algebraic'' and ''geometric'' intersection number of $f_1$ and $f_2$. | + | This clasical fact is either a theorem or a definition depending on which definition of [[Intersection_form#Definition|homology intersection pairing]] one accepts. For a proof see \cite{Scorpan2005|Section 3.2} or \cite{Ranicki2002|Proposition 7.22}. Unless this equality is a definition, the left- and right- hand sides of the equality can be called ''algebraic'' and ''geometric'' intersection number of $f_1$ and $f_2$. |
<!-- | <!-- | ||
$\lambda^{\mathrm{geo}}(N_1,N_2)$ defined below. | $\lambda^{\mathrm{geo}}(N_1,N_2)$ defined below. | ||
Latest revision as of 15:17, 2 April 2019
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Introduction
Let  be a connected oriented manifold of dimension
be a connected oriented manifold of dimension 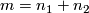 and
and 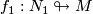 ,
, 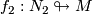 immersions of oriented
immersions of oriented 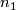 - and
- and 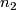 -manifolds. The intersection number of
-manifolds. The intersection number of  and
and  counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
This page is based on [Ranicki2002], see also [Broecker&Jaenich1982, Excercise 14.9.6].
[edit] 2 Statement
Let
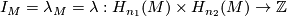
be the homology intersection pairing (or product) of  .
.
The double point set of  and
and  is defined by
is defined by
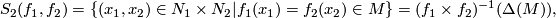
where 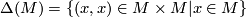 the diagonal.
the diagonal.
A double point 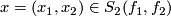 of
of  and
and  is transverse if the linear map
is transverse if the linear map

is an isomorphism.
Immersions  and
and  are transverse (or have transverse intersection) if
are transverse (or have transverse intersection) if 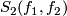 is finite and every double point is transverse.
is finite and every double point is transverse.
The index, or the sign 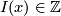 of a transverse double point
of a transverse double point 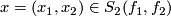 is
is
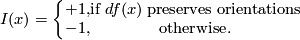
Theorem 2.1. If  and
and  are transverse, then
are transverse, then
![\displaystyle \lambda(f_{1*}[N_1],f_{2*}[N_2])=\sum_{x\in S_2(f_1,f_2)}{I(x)}.](/images/math/6/a/d/6adfe6a8168c927468d1cb8f9c5c707d.png)
This clasical fact is either a theorem or a definition depending on which definition of homology intersection pairing one accepts. For a proof see [Scorpan2005, Section 3.2] or [Ranicki2002, Proposition 7.22]. Unless this equality is a definition, the left- and right- hand sides of the equality can be called algebraic and geometric intersection number of  and
and  .
.
[edit] References
- [Broecker&Jaenich1982] Th. Br\"ocker and K. J\"anich Introduction to Differential Topology, Cambridge University Press, 1982. ISBN-13: 978-0521284707, ISBN-10: 0521284708.
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
- [Scorpan2005] A. Scorpan, The wild world of 4-manifolds, American Mathematical Society, 2005. MR2136212 (2006h:57018) Zbl 1075.57001