Intersection number of immersions
Askopenkov (Talk | contribs) |
Askopenkov (Talk | contribs) |
||
| Line 12: | Line 12: | ||
$$I_M=\lambda_M=\lambda: H_{n_1}(M)\times H_{n_2}(M) \to \Z$$ | $$I_M=\lambda_M=\lambda: H_{n_1}(M)\times H_{n_2}(M) \to \Z$$ | ||
the [[Intersection_form#Definition|''homology intersection pairing (or product)'']] of $M$. | the [[Intersection_form#Definition|''homology intersection pairing (or product)'']] of $M$. | ||
| + | |||
| + | Let $N_i$ be oriented $n_i$-manifolds $(i=1,2)$. | ||
| + | The ''double point set'' of maps $f_i:N_i\to M$ $(i=1,2)$ is defined by | ||
| + | $$S_2(f_1,f_2) = \{(x_1,x_2)\in N_1\times N_2 | f_1(x_1) = f_2(x_2)\in M\} = | ||
| + | (f_1\times f_2)^{-1}(\Delta(M)),$$ | ||
| + | where $\Delta(M) = \{(x,x)\in M\times M | x\in M\}$ the diagonal. | ||
| + | |||
| + | A double point $x=(x_1,x_2)\in S_2(f_1,f_2)$ of immersions $f_i:N_i\looparrowright M$ $(i=1,2)$ is ''transverse'' if the linear map | ||
| + | $$df(x) = df_1(x_1)\oplus df_2(x_2): \tau_{N_1}(x_1)\oplus \tau_{N_2}(x_2) \to \tau_M(f(x))$$ | ||
| + | is an isomorphism. | ||
| + | Immersions $f_i:N_i\looparrowright M$ $(i=1,2)$ have ''transverse intersection'' (or are ''transverse'') if $S_2(f_1,f_2)$ is finite and every double point is transverse. | ||
| + | |||
| + | The ''index'', or the ''sign'' $I(x)\in\Z$ of a transverse double point $x=(x_1,x_2)\in S_2(f_1,f_2)$ is | ||
| + | $$I(x) = \left\{ \begin{array}{cc} +1, & \mathrm{if}\; df(x)\; \mathrm{preserves}\; \mathrm{orientations}\\ -1, & \mathrm{otherwise}.\end{array}\right.$$ | ||
{{beginthm|Theorem}}\label{t:algeo} | {{beginthm|Theorem}}\label{t:algeo} | ||
| − | For any immersions $f_1:N_1\looparrowright M$, $f_2:N_2\looparrowright M$ of oriented $n_1$- and $n_2$-manifolds | + | For any transverse immersions $f_1:N_1\looparrowright M$, $f_2:N_2\looparrowright M$ of oriented $n_1$- and $n_2$-manifolds |
| + | $$\lambda(f_{1*}[N_1],f_{2*}[N_2])=\sum_{x\in S_2(f_1,f_2)}{I(x)}.$$ | ||
{{endthm}} | {{endthm}} | ||
This this clasical fact is either a theorem or a definition depending on which definition of homology intersection pairing one accepts. | This this clasical fact is either a theorem or a definition depending on which definition of homology intersection pairing one accepts. | ||
For a proof see \cite{Scorpan2005|Section 3.2} or \cite{Ranicki2002|Proposition 7.22}. | For a proof see \cite{Scorpan2005|Section 3.2} or \cite{Ranicki2002|Proposition 7.22}. | ||
| − | + | Unless this equality is a definition, the left- and right- hand sides of the equality can be called ''algebraic'' and ''geometric'' intersection number of $f_1$ and $f_2$. | |
| − | + | ||
<!-- | <!-- | ||
| + | $\lambda^{\mathrm{geo}}(N_1,N_2)$ defined below. | ||
$\lambda^{\mathrm{alg}}(f_1,f_2)\in\Z$ $$\lambda^{\mathrm{alg}}(N_1,N_2) := \lambda((f_1)_*[N_1],(f_2)_*[N_2]).$$ | $\lambda^{\mathrm{alg}}(f_1,f_2)\in\Z$ $$\lambda^{\mathrm{alg}}(N_1,N_2) := \lambda((f_1)_*[N_1],(f_2)_*[N_2]).$$ | ||
the homology intersection of the homology classes $(f_1)_*[N_1]\in H_{n_1}(M)$, $(f_2)_*[N_2]\in H_{n_2}(M)$: | the homology intersection of the homology classes $(f_1)_*[N_1]\in H_{n_1}(M)$, $(f_2)_*[N_2]\in H_{n_2}(M)$: | ||
| − | |||
==Alternative description== | ==Alternative description== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The ''geometric'' intersection number of transverse immersions $f_i:N_i\looparrowright M$ $(i=1,2)$ is defined as | The ''geometric'' intersection number of transverse immersions $f_i:N_i\looparrowright M$ $(i=1,2)$ is defined as | ||
$$\lambda^{\mathrm{geo}}(N_1,N_2) = \sum_{x\in S_2(f_1,f_2)}{I(x)}\in \Z.$$ | $$\lambda^{\mathrm{geo}}(N_1,N_2) = \sum_{x\in S_2(f_1,f_2)}{I(x)}\in \Z.$$ | ||
| − | + | The algebraic and geometric intersection numbers agree, | |
| − | + | ||
| − | + | ||
$$\lambda^{\mathrm{alg}}(N_1,N_2)=\lambda^{\mathrm{geo}}(N_1,N_2).$$ --> | $$\lambda^{\mathrm{alg}}(N_1,N_2)=\lambda^{\mathrm{geo}}(N_1,N_2).$$ --> | ||
| − | |||
==References== | ==References== | ||
Revision as of 14:52, 2 April 2019
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
This page is based on [Ranicki2002], see also [Broecker&Jaenich1982, Excercise 14.9.6]. Let 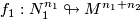 ,
, 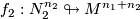 be immersions of oriented manifolds in a connected oriented manifold. The intersection number
be immersions of oriented manifolds in a connected oriented manifold. The intersection number ![\lambda([N_1],[N_2])\in\Z](/images/math/b/9/8/b9827bb99377a741b1c53c8e38e54871.png) has both an algebraic and geometric formulation; roughly speaking it counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
The intersection number of immersions is closely related to the intersection form of a manifold (and so to the signature of a
has both an algebraic and geometric formulation; roughly speaking it counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
The intersection number of immersions is closely related to the intersection form of a manifold (and so to the signature of a  -dimensional manifold) and to characteristic classes.
These are important invariants used in the classification of manifolds.
-dimensional manifold) and to characteristic classes.
These are important invariants used in the classification of manifolds.
2 Statement
Let  be a connected oriented manifold of dimension
be a connected oriented manifold of dimension 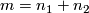 and
and
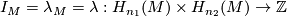
the homology intersection pairing (or product) of  .
.
Let 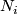 be oriented
be oriented 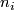 -manifolds
-manifolds 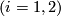 .
The double point set of maps
.
The double point set of maps 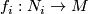
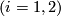 is defined by
is defined by
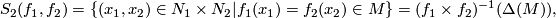
where 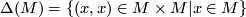 the diagonal.
the diagonal.
A double point 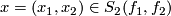 of immersions
of immersions 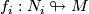
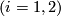 is transverse if the linear map
is transverse if the linear map

is an isomorphism.
Immersions 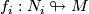
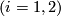 have transverse intersection (or are transverse) if
have transverse intersection (or are transverse) if 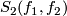 is finite and every double point is transverse.
is finite and every double point is transverse.
The index, or the sign 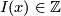 of a transverse double point
of a transverse double point 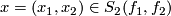 is
is
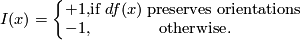
Theorem 2.1.
For any transverse immersions 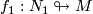 ,
, 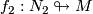 of oriented
of oriented 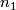 - and
- and 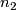 -manifolds
-manifolds
![\displaystyle \lambda(f_{1*}[N_1],f_{2*}[N_2])=\sum_{x\in S_2(f_1,f_2)}{I(x)}.](/images/math/6/a/d/6adfe6a8168c927468d1cb8f9c5c707d.png)
This this clasical fact is either a theorem or a definition depending on which definition of homology intersection pairing one accepts.
For a proof see [Scorpan2005, Section 3.2] or [Ranicki2002, Proposition 7.22].
Unless this equality is a definition, the left- and right- hand sides of the equality can be called algebraic and geometric intersection number of  and
and 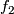 .
.
References
- [Broecker&Jaenich1982] Th. Br\"ocker and K. J\"anich Introduction to Differential Topology, Cambridge University Press, 1982. ISBN-13: 978-0521284707, ISBN-10: 0521284708.
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
- [Scorpan2005] A. Scorpan, The wild world of 4-manifolds, American Mathematical Society, 2005. MR2136212 (2006h:57018) Zbl 1075.57001