Intersection number of immersions
Askopenkov (Talk | contribs) (→Introduction) |
Askopenkov (Talk | contribs) (→Definition) |
||
| Line 9: | Line 9: | ||
== Definition == | == Definition == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $M$ be an oriented $m$-dimensional manifold. | + | Let $M$ be an oriented $m$-dimensional manifold. |
| − | + | We use the [[Intersection_form#Definition|''homology intersection pairing (or product)'']] of $M$, | |
| − | + | $$I_M=\lambda_M=\lambda: H_n(M)\times H_{m-n}(M) \to \Z; \quad (x,y) \mapsto \lambda(x,y).$$ | |
| − | $$ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
The '''algebraic intersection number''' $\lambda^{\mathrm{alg}}(f_1,f_2)\in\Z$ of immersions of oriented manifolds $f_1:N_1^{n_1} \looparrowright M^{n_1+n_2}$, $f_2:N_2^{n_2} \looparrowright M^{n_1+n_2}$ in a connected oriented manifold, is the homology intersection of the homology classes $(f_1)_*[N_1]\in H_{n_1}(M)$, $(f_2)_*[N_2]\in H_{n_2}(M)$: | The '''algebraic intersection number''' $\lambda^{\mathrm{alg}}(f_1,f_2)\in\Z$ of immersions of oriented manifolds $f_1:N_1^{n_1} \looparrowright M^{n_1+n_2}$, $f_2:N_2^{n_2} \looparrowright M^{n_1+n_2}$ in a connected oriented manifold, is the homology intersection of the homology classes $(f_1)_*[N_1]\in H_{n_1}(M)$, $(f_2)_*[N_2]\in H_{n_2}(M)$: | ||
$$\lambda^{\mathrm{alg}}(N_1,N_2) := \lambda((f_1)_*[N_1],(f_2)_*[N_2]).$$ | $$\lambda^{\mathrm{alg}}(N_1,N_2) := \lambda((f_1)_*[N_1],(f_2)_*[N_2]).$$ | ||
Revision as of 13:47, 29 March 2019
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
This page is based on [Ranicki2002]. Let 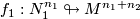 ,
, 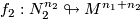 be immersions of oriented manifolds in a connected oriented manifold. The intersection number
be immersions of oriented manifolds in a connected oriented manifold. The intersection number ![\lambda([N_1],[N_2])\in\Z](/images/math/b/9/8/b9827bb99377a741b1c53c8e38e54871.png) has both an algebraic and geometric formulation; roughly speaking it counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
The intersection number of immersions is closely related to the intersection form of a manifold (and so to the signature of a
has both an algebraic and geometric formulation; roughly speaking it counts with sign the number of intersection points that the two immersions have. The intersection number is an obstruction to perturbing the immersions into being disjoint. When it vanishes this perturbation can often be achieved using the Whitney trick.
The intersection number of immersions is closely related to the intersection form of a manifold (and so to the signature of a 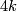 -dimensional manifold) and to characteristic classes.
These are important invariants used in the classification of manifolds.
-dimensional manifold) and to characteristic classes.
These are important invariants used in the classification of manifolds.
2 Definition
Let  be an oriented
be an oriented  -dimensional manifold.
We use the homology intersection pairing (or product) of
-dimensional manifold.
We use the homology intersection pairing (or product) of  ,
,
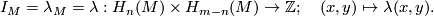
The algebraic intersection number 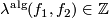 of immersions of oriented manifolds
of immersions of oriented manifolds 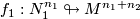 ,
, 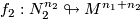 in a connected oriented manifold, is the homology intersection of the homology classes
in a connected oriented manifold, is the homology intersection of the homology classes ![(f_1)_*[N_1]\in H_{n_1}(M)](/images/math/5/0/9/509ee0909398b7f1fdcd3ac61033f43e.png) ,
, ![(f_2)_*[N_2]\in H_{n_2}(M)](/images/math/6/5/2/6526c09939b70b354f1e605991ddea1b.png) :
:
![\displaystyle \lambda^{\mathrm{alg}}(N_1,N_2) := \lambda((f_1)_*[N_1],(f_2)_*[N_2]).](/images/math/4/b/8/4b8c399582236de311aa3eb060ed9393.png)
3 Alternative description
The double point set of maps 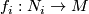
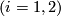 is defined by
is defined by
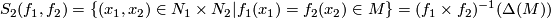
with 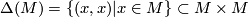 the diagonal subspace.
the diagonal subspace.
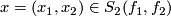 of immersions
of immersions 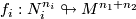
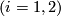 is transverse if the linear map
is transverse if the linear map 
Immersions 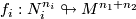
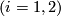 have transverse intersections (or are transverse) if each double point is transverse and
have transverse intersections (or are transverse) if each double point is transverse and 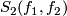 is finite.
is finite.
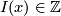 of a transverse double point
of a transverse double point 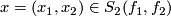 is
is 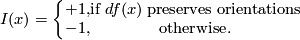
The geometric intersection number of transverse immersions 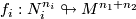
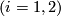 is
is
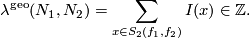
4 Equivalence of definitions
The algebraic and geometric intersection numbers agree,
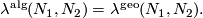
For a proof of this clasical fact see [Scorpan2005, Section 3.2] or [Ranicki2002, Proposition 7.22].
5 References
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
- [Scorpan2005] A. Scorpan, The wild world of 4-manifolds, American Mathematical Society, 2005. MR2136212 (2006h:57018) Zbl 1075.57001