Immersion
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:15, 16 May 2013 and the changes since publication. |
|
The user responsible for this page is Ulrich Koschorke. No other user may edit this page at present. |
Contents |
1 Definition
We work in a fixed category CAT of topological, piecewise linear, 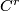 -differentiable
-differentiable 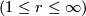 or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them.
or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them. 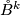 denotes the open unit ball in
denotes the open unit ball in 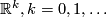 .
.
Let 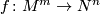 be such a map between manifolds of the indicated dimensions
be such a map between manifolds of the indicated dimensions 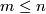 .
.
Definition 1.1.
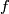 is a local immersion at a point
is a local immersion at a point 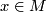 if there exist open neighbourhoods
if there exist open neighbourhoods 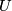 of
of  and
and 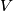 of
of 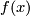 in
in  and
and 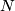 , resp., such that
, resp., such that 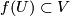 and:
and:
- there is a CAT-isomorphism
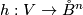 (i.e. both
(i.e. both 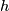 and
and 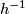 are CAT-maps) which maps
are CAT-maps) which maps 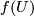 onto
onto 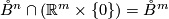 ; and
; and
-
 yields a CAT-isomorphism from
yields a CAT-isomorphism from 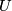 onto
onto 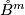 .
.
We call f an immersion (and we write 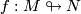 ) if
) if 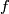 is a local immersion at every point
is a local immersion at every point 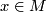 .
.
Thus an immersion looks locally like the inclusion  of Euclidean spaces. It allows us to visualize a given manifold
of Euclidean spaces. It allows us to visualize a given manifold  in a possibly more familar setting such as
in a possibly more familar setting such as 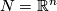 . E.g. the projective plane
. E.g. the projective plane 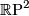 can be visualized in
can be visualized in 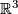 with the help of the Boy's surface, the image of a
with the help of the Boy's surface, the image of a 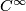 -immersion: see for example the page on surfaces.
The following two questions play an important role.
-immersion: see for example the page on surfaces.
The following two questions play an important role.
- Existence: Given
 and
and 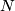 , is there any immersion
, is there any immersion 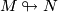 at all?
at all?
- Classification: How many `essentially different´ immersions exist?
2 The smooth case
This section is about the category of smooth, i.e. 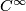 , manifolds and maps. It follows from the inverse function theorem that a smooth map
, manifolds and maps. It follows from the inverse function theorem that a smooth map 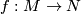 between smooth manifolds is a local immersion at
between smooth manifolds is a local immersion at 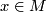 precisely if the tangent map
precisely if the tangent map 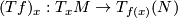 is injective. Thus
is injective. Thus 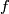 is a smooth immersion if and only if it induces a vector bundle monomorphism
is a smooth immersion if and only if it induces a vector bundle monomorphism 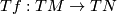 . E.g. the figure
. E.g. the figure  cannot be the image of a smooth immersion, due to the two sharp corners which don't allow a well-defined tangent line. However there exists a smooth immersion
cannot be the image of a smooth immersion, due to the two sharp corners which don't allow a well-defined tangent line. However there exists a smooth immersion 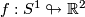 with image the figure
with image the figure  .
.
Theorem 2.1 [Hirsch1959], [Smale1959a], Phillips 1967.
If (i) 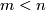 , or if (ii)
, or if (ii)  is open and
is open and 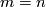 , then the map
, then the map
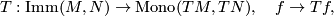
is a weak homotopy equivalence. Here the space, 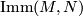 , of all smooth immersions
, of all smooth immersions 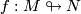 and
and 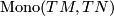 , the space of all vector bundle monomorphisms
, the space of all vector bundle monomorphisms 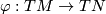 , are endowed respectively with the
, are endowed respectively with the 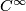 -topology and the compact-open topology.
-topology and the compact-open topology.
Remark 2.2. For a good exposition of Theorem 2.1 see [Adachi1993, pp.87 and 93].
Corollary 2.3.
Under the assumptions of theorem 2.1 there exists an immersion 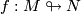 if and only if there is a vector bundle monomorphism from the tangent bundle
if and only if there is a vector bundle monomorphism from the tangent bundle 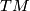 of
of  to
to 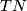 . E. g. if
. E. g. if  is parallelizable (i. e.
is parallelizable (i. e. 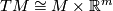 ) then
) then 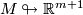 .
.
Theorem 2.4 [Whitney1944a] .
If 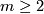 then there exists an immersion
then there exists an immersion 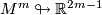 (E. g. any surface can be immersed into
(E. g. any surface can be immersed into 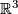 ).
).
Remark 2.5. See also e.g. [Adachi1993, p. 86ff].
Theorem 2.4 is best possible as long as we put no restrictions on  .
.
Example 2.6.
The real projective space 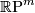 cannot be immersed into
cannot be immersed into 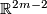 if
if 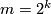 . This follows from an easy calculation using Stiefel-Whitney classes: see, [Milnor&Stasheff1974, Theorem 4,8].
. This follows from an easy calculation using Stiefel-Whitney classes: see, [Milnor&Stasheff1974, Theorem 4,8].
Definition 2.7.
Two immersions 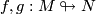 are regularly homotopic if there exists a smooth map
are regularly homotopic if there exists a smooth map 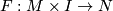 which with
which with 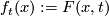 satisfies the following:
satisfies the following:
-
 ;
;
-
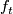 is a immersion for all
is a immersion for all 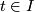 .
.
Corollary 2.8.
Assume 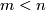 . Two immersions
. Two immersions 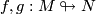 are regularly homotopic if and only if their tangent maps
are regularly homotopic if and only if their tangent maps 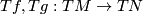 are homotopic through vector bundle monomorphisms.
are homotopic through vector bundle monomorphisms.
Example 2.9 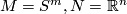 , [Smale1959a].
The regular homotopy classes of immersions
, [Smale1959a].
The regular homotopy classes of immersions 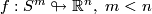 , are in one-to-one correspondance with the elements of the homotopy group
, are in one-to-one correspondance with the elements of the homotopy group 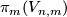 , where
, where 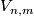 is the Stiefel manifold of
is the Stiefel manifold of  -frames in
-frames in 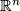 . In particular, all immersions
. In particular, all immersions 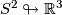 are regularly homotopic (since
are regularly homotopic (since 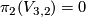 ). E. g. the standard inclusion
). E. g. the standard inclusion 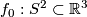 is regularly homotopic to
is regularly homotopic to 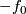 ; i. e. you can turn the sphere inside out in
; i. e. you can turn the sphere inside out in 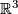 , with possible self-intersections but without creating any crease.
, with possible self-intersections but without creating any crease.
Remark 2.10. The Smale-Hirsch theorem makes existence and classification problems accessible to standard methods of algebraic topology such as classical obstruction theorem (cf. e.g. [Steenrod1951]), characteristic classes (cf. e.g. [Milnor&Stasheff1974]), Postnikov towers, the singularity method (cf. e.g. [Koschorke1981]) etc.: see [Smale1963] for the state of the art in 1963.
3 Self intersections
It is a characteristic feature of immersions - as compared to embeddings - that  -tuple selfintersections may occur for some
-tuple selfintersections may occur for some 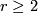 , i. e. points in
, i. e. points in 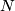 which are the image of at least
which are the image of at least  distinct elements of M (e. g. the double point in the figure 8
immersion
distinct elements of M (e. g. the double point in the figure 8
immersion 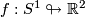 with image
with image  ). Generically the locus of r-tuple points of a smooth immersion
). Generically the locus of r-tuple points of a smooth immersion 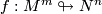 is an immersed (
is an immersed (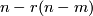 )-dimensional manifold in
)-dimensional manifold in 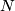 . Its properties may yield a variety of interesting invariants which link immersions to other concepts of topology. E. g. let
. Its properties may yield a variety of interesting invariants which link immersions to other concepts of topology. E. g. let 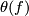 denote the
denote the 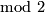 number of (
number of (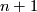 )-tuple points of a selftransverse immersion
)-tuple points of a selftransverse immersion 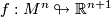 .
.
Theorem 3.1 [Eccles1981] .
Given a natural number 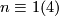 , there is an
, there is an 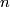 -dimensional closed smooth manifold
-dimensional closed smooth manifold 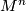 and an immersion
and an immersion 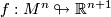 satisfying
satisfying 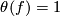 if and only if there exists a framed (
if and only if there exists a framed (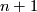 )-dimensional manifold with Kervaire invariant
)-dimensional manifold with Kervaire invariant 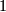 .
.
According to [Hill&Hopkins&Ravenel2009] (and previous authors) this holds precisely when 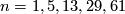 or possibly
or possibly 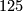 . If
. If 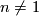 and
and 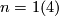 the manifold
the manifold  in question cannot be orientable (cf. [Eccles1981]). Thus the figure 8 immersion
in question cannot be orientable (cf. [Eccles1981]). Thus the figure 8 immersion 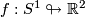 plays a rather special role here.
plays a rather special role here.
4 References
- [Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
- [Eccles1981] P. J. Eccles, Codimension one immersions and the Kervaire invariant one problem, Math. Proc. Cambridge Philos. Soc. 90 (1981), no.3, 483–493. MR628831 (83c:57015) Zbl 0479.57016
- [Hill&Hopkins&Ravenel2009] M. A. Hill, M. J. Hopkins and D. C. Ravenel, On the non-existence of elements of Kervaire invariant one, (2009). Available at the arXiv:0908.3724.
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Koschorke1981] U. Koschorke, Vector fields and other vector bundle morphisms-a singularity approach, Springer, 1981. MR611333 (82i:57026) Zbl 0459.57016
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Smale1959a] S. Smale, The classification of immersions of spheres in Euclidean spaces, Ann. of Math. (2) 69 (1959), 327–344. MR0105117 (21 #3862) Zbl 0089.18201
- [Smale1963] S. Smale, A survey of some recent developments in differential topology, Bull. Amer. Math. Soc. 69 (1963), 131–145. MR0144351 (26 #1896) Zbl 0133.16507
- [Steenrod1951] N. Steenrod, The topology of fibre bundles., (Princeton Mathematical Series No. 14.) Princeton: Princeton University Press. VIII, 224 p. , 1951. MR1688579 (2000a:55001) Zbl 0054.07103
- [Whitney1944a] H. Whitney, The singularities of a smooth
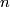 -manifold in
-manifold in 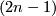 -space, Ann. of Math. (2) 45 (1944), 247–293. MR0010275 (5,274a) Zbl 0063.08238
-space, Ann. of Math. (2) 45 (1944), 247–293. MR0010275 (5,274a) Zbl 0063.08238
5 External links
- The Encyclopedia of Mathematics article on an immersion of manifold
- The Wikipedia page about immersions