Hyperbolic Surfaces
(Created page with "<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - Fo...") |
|||
| Line 19: | Line 19: | ||
== Construction and examples == | == Construction and examples == | ||
<wikitex>; | <wikitex>; | ||
| + | |||
| + | <div class="thumb tright"><div class="thumbinner" style="width:214px;"><a href="/File:Polygon_construction.png" class="image"><img alt="" src="/images/5/5e/Polygon_construction.png" width="212" height="207" class="thumbimage" /></a><div class="thumbcaption"> | ||
| + | |||
| + | <div class="magnify"> | ||
| + | <a href="/File:Polygon_construction.png" class="internal" title="Enlarge"> | ||
| + | <img src="/skins/common/images/magnify-clip.png" width="15" height="11" alt="" /> | ||
| + | </a> | ||
| + | </div>The orientable surface of genus 2 can be obtained by identifying edges in a regular octagon. | ||
| + | </div> | ||
| + | </div> | ||
| + | </div> | ||
Any hyperbolic metric on a closed, orientable surface $S_g$ of genus $g\ge 2$ is obtained by the following | Any hyperbolic metric on a closed, orientable surface $S_g$ of genus $g\ge 2$ is obtained by the following | ||
Revision as of 11:10, 29 October 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
...
2 Construction and examples
<a href="/File:Polygon_construction.png" class="internal" title="Enlarge"> <img src="/skins/common/images/magnify-clip.png" width="15" height="11" alt="" /> </a>
Any hyperbolic metric on a closed, orientable surface 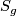 of genus
of genus 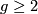 is obtained by the following
construction: choose a geodesic
is obtained by the following
construction: choose a geodesic 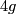 -gon in the hyperbolic plane
-gon in the hyperbolic plane 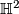 with area
with area 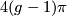 . (This implies that the sum of interior angles is
. (This implies that the sum of interior angles is 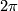 .) Then choose orientation-preserving isometries
.) Then choose orientation-preserving isometries 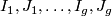 which realise the gluing pattern of
which realise the gluing pattern of 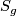 : for
: for 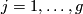 we require that
we require that 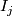 maps
maps 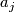 to
to 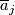 ,
, 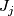 maps
maps 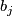 to
to 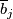 . Let
. Let 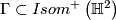 be the subgroup generated by
be the subgroup generated by 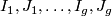 . Then
. Then 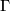 is a discrete subgroup of
is a discrete subgroup of 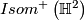 and
and 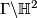 is a hyperbolic surface diffeomorphic to
is a hyperbolic surface diffeomorphic to 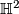 .
.
The moduli space of hyperbolic metrics on the closed, orientable surface 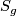 is
is 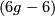 -dimensional.
-dimensional.
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...