Hyperbolic 3-manifolds
| Line 35: | Line 35: | ||
== Invariants == | == Invariants == | ||
<wikitex>; | <wikitex>; | ||
| + | By Mostow rigidity, complete hyperbolic metrics of finite volume on a 3-manifold are unique up to isometry. This implies that geometric invariants of the hyperbolic metric, such as the volume and the Chern-Simons-invariant, are topological invariants. | ||
... | ... | ||
</wikitex> | </wikitex> | ||
| Line 40: | Line 41: | ||
== Classification/Characterization == | == Classification/Characterization == | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | By the Marden tameness conjecture (proved by Agol and Calegari-Gabai) each hyperbolic 3-manifold with finitely generated fundamental group is the interior of a compact 3-manifold with boundary. |
| + | <br> | ||
| + | <br>If $M$ is an orientable 3-manifold with boundary, whose interior admits a complete hyperbolic metric of finite volume, then $\partial M$ is a (possibly empty) union of incompressible tori. | ||
| + | <br> | ||
| + | <br>Ends of infinite volume fall into two classes, geometrically finite ends and geometrically infinite ends.... | ||
</wikitex> | </wikitex> | ||
Revision as of 20:14, 1 April 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A 3-manifold is hyperbolic if it satisfies the following (equivalent) conditions:
- it admits a complete Riemannian metric of sectional curvature constant -1,
- it admits a Riemannian metric such that its universal covering (with the pull-back metric) is isometric to hyperbolic 3-space 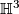 ,
,
- it is homeomorphic to 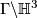 , for some discrete, torsion-free group of isometries of hyperbolic 3-space.
, for some discrete, torsion-free group of isometries of hyperbolic 3-space.
Here, hyperbolic 3-space 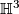 is the simply connected, complete, Riemannian manifold with sectional curvature constant -1. By Cartans Theorem,
is the simply connected, complete, Riemannian manifold with sectional curvature constant -1. By Cartans Theorem, 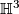 is unique up to isometry. There are different models for
is unique up to isometry. There are different models for 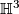 , like the upper half-space model, the Poincaré disc model or the hyperboloid model.
, like the upper half-space model, the Poincaré disc model or the hyperboloid model.
The ideal boundary 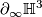 can be identified with projective space
can be identified with projective space 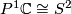 . Isometries of hyperbolic 3-space act as conformal automorphisms of the ideal boundary. Thus we can identify the isometry group
. Isometries of hyperbolic 3-space act as conformal automorphisms of the ideal boundary. Thus we can identify the isometry group 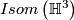 with the group of conformal automorphisms
with the group of conformal automorphisms 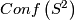 .
.
The group 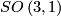 acts on the hyperboloid model and one can use this action to identify
acts on the hyperboloid model and one can use this action to identify 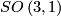 with the index two subgroup
with the index two subgroup 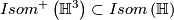 of orientation-preserving isometries. The action is transitive and has
of orientation-preserving isometries. The action is transitive and has 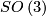 as a point stabilizer, thus
as a point stabilizer, thus 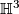 is isometric to the homogeneous space
is isometric to the homogeneous space 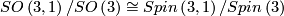 .
.
The group 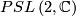 acts by fractional-linear automorphisms on
acts by fractional-linear automorphisms on 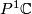 . This action on
. This action on 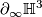 uniquely extends to an action on
uniquely extends to an action on 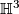 by orientation-preserving isometries. One can use this action to identify
by orientation-preserving isometries. One can use this action to identify 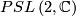 with
with
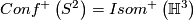 .
The action is transitive and has
.
The action is transitive and has 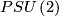 as a point stabilizer, thus
as a point stabilizer, thus 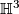 is isometric to the homogeneous space
is isometric to the homogeneous space 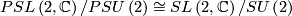 .
.
Thus, if  is oriented, then there are two more equivalent conditions:
is oriented, then there are two more equivalent conditions:
An oriented 3-manifold is hyperbolic if and only if
- it is homeomorphic to 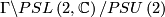 for some discrete, torsion-free subgroup
for some discrete, torsion-free subgroup 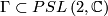 ,
,
-
it is homeomorphic to 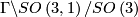 for some discrete, torsion-free subgroup
for some discrete, torsion-free subgroup 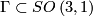 .
.
2 Construction and examples
...
3 Invariants
By Mostow rigidity, complete hyperbolic metrics of finite volume on a 3-manifold are unique up to isometry. This implies that geometric invariants of the hyperbolic metric, such as the volume and the Chern-Simons-invariant, are topological invariants. ...
4 Classification/Characterization
By the Marden tameness conjecture (proved by Agol and Calegari-Gabai) each hyperbolic 3-manifold with finitely generated fundamental group is the interior of a compact 3-manifold with boundary.
If  is an orientable 3-manifold with boundary, whose interior admits a complete hyperbolic metric of finite volume, then
is an orientable 3-manifold with boundary, whose interior admits a complete hyperbolic metric of finite volume, then 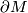 is a (possibly empty) union of incompressible tori.
is a (possibly empty) union of incompressible tori.
Ends of infinite volume fall into two classes, geometrically finite ends and geometrically infinite ends....
5 Further discussion
...