Hirsch-Smale theory
| Line 29: | Line 29: | ||
If $n=k+1=2$, then conditions for the extendibility of $\left(f,f^\prime\right)$ are given in {{cite|Blank1967}}, more details are worked out in {{cite|Frisch2010}}. | If $n=k+1=2$, then conditions for the extendibility of $\left(f,f^\prime\right)$ are given in {{cite|Blank1967}}, more details are worked out in {{cite|Frisch2010}}. | ||
| + | |||
| + | |||
| + | ==Applications== | ||
| + | |||
| + | {{beginthm|Theorem |}} | ||
| + | Let $M$ be a smooth manifold of dimension $k<n$. Then the following assertions are equivalent: | ||
| + | |||
| + | (i) $M$ can be immersed into ${\mathbb R}^n$, | ||
| + | |||
| + | (ii) there exists a $GL\left(k,{\mathbb R}\right)$-equivariant map $T_k\left(M\right)\rightarrow V_{n,k}$, where $T_k\left(M\right)\rightarrow M$ is the $k$-frame bundle and $V_{n,k}$ is the Stiefel manifold, | ||
| + | |||
| + | (iii) the bundle associated to $T_k\left(M\right)$ with fiber $V_{n,k}$ has a cross section. | ||
| + | {{endthm}} | ||
| + | {{cite|Hirsch1959}}, Theorem 6.1. | ||
| + | The equivalence between (i) and (ii) is proved by induction over the dimension of subsimplices in a triangulation of $M$ using Theorem 3.9 (which can be adapted from $\left(D^k,S^{k-1}\right)$ to $\left(\Delta^k,\partial \Delta^k\right)$) for the inductive step. The equivalence between (ii) and (iii) is a general fact from the theory of fiber bundles. | ||
| + | {{beginthm|Corollary |}} Parallelizable $k$-manifolds can be immersed into ${\mathbb R}^{k+1}$.{{endthm}} | ||
| + | |||
| + | {{beginthm|Corollary |}} Exotic $7$-spheres can be immersed into ${\mathbb R}^8$.{{endthm}} | ||
| + | |||
| + | |||
==References== | ==References== | ||
Revision as of 20:19, 6 July 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Hirsch-Smale theory is the name now given to the study of regular homotopy classes of immersions and more generally the space of immersions via their derivative maps. It is one of the spectacular success stories of geometric topology and in particular the h-principle.
2 Results
Definition 2.1. For a submanifold 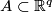 and a manifold
and a manifold  , a pair
, a pair 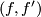 is called an
is called an 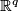 -immersion if
-immersion if
- 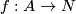 is an immersion,
is an immersion,
- 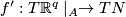 is a linear map, and
is a linear map, and
- there exists an open neighborhood  of
of  in
in 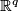 and an immersion
and an immersion 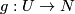 such that
such that 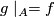 and
and 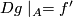 .
.
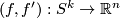 be an
be an 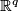 -immersion. The obstruction to extending
-immersion. The obstruction to extending 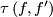 , denoted by
, denoted by 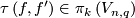 with
with 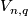 the Stiefel manifold of
the Stiefel manifold of  -frames in
-frames in 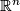 , is the homotopy class of
, is the homotopy class of 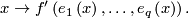
Theorem 2.3. Let 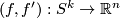 be a smooth
be a smooth 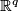 -immersion.
-immersion.
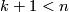 and
and 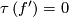 , then
, then 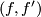 can be extended to an
can be extended to an 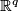 -immersion
-immersion 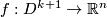 .
. [Hirsch1959], Theorem 3.9.
This Theorem does not hold for 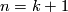 .
.
If 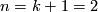 , then conditions for the extendibility of
, then conditions for the extendibility of 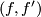 are given in [Blank1967], more details are worked out in [Frisch2010].
are given in [Blank1967], more details are worked out in [Frisch2010].
1 Applications
Theorem 4.1.
Let  be a smooth manifold of dimension
be a smooth manifold of dimension  . Then the following assertions are equivalent:
. Then the following assertions are equivalent:
(i)  can be immersed into
can be immersed into 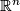 ,
,
(ii) there exists a 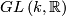 -equivariant map
-equivariant map 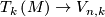 , where
, where 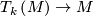 is the
is the  -frame bundle and
-frame bundle and 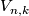 is the Stiefel manifold,
is the Stiefel manifold,
(iii) the bundle associated to 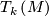 with fiber
with fiber 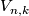 has a cross section.
has a cross section.
[Hirsch1959], Theorem 6.1.
The equivalence between (i) and (ii) is proved by induction over the dimension of subsimplices in a triangulation of  using Theorem 3.9 (which can be adapted from
using Theorem 3.9 (which can be adapted from 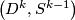 to
to 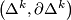 ) for the inductive step. The equivalence between (ii) and (iii) is a general fact from the theory of fiber bundles.
) for the inductive step. The equivalence between (ii) and (iii) is a general fact from the theory of fiber bundles.
 -manifolds can be immersed into
-manifolds can be immersed into 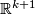 .
. -spheres can be immersed into
-spheres can be immersed into 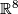 .
.
2 References
- [Blank1967] Samuel Joel Blank, Extending Immersions and regular Homotopies in Codimension 1, PhD Thesis Brandeis University, 1967.
- [Frisch2010] Dennis Frisch, Classification of Immersions which are bounded by Curves in Surfaces, PhD Thesis TU Darmstadt, 2010.
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603