High codimension links
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
Contents |
1 Introduction
This page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings.
We describe classification of embeddings 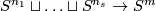 for
for 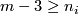 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
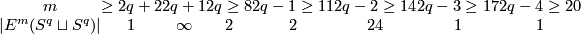
For an  -tuple
-tuple  denote
denote 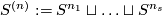 . Although
. Although 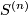 is not a manifold when
is not a manifold when 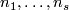 are not all equal, embeddings
are not all equal, embeddings 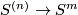 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 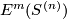 the set of embeddings
the set of embeddings 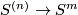 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 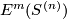 for
for 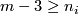 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 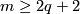 , any two embeddings
, any two embeddings 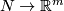 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 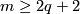 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 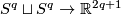 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 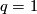 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 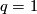 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
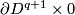 and
and 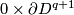 in
in 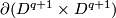 ;
;
- or given by equations:
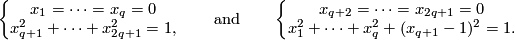
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 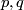 one constructs an embedding
one constructs an embedding 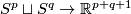 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
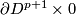 and
and 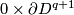 in
in 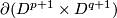 .
.
- or given by equations:
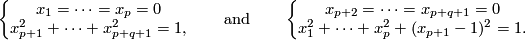
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
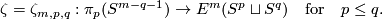
Denote by 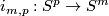 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 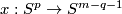 representing an element of
representing an element of 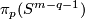 let
let
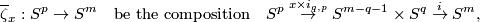
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 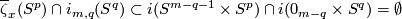 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
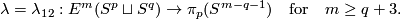
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding  such that
such that 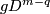 intersects
intersects 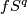 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 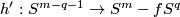 of
of  to
to 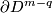 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 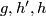 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 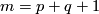 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 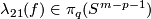 for
for 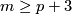 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 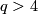 , if the restriction of
, if the restriction of  to
to 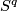 is unknotted).
is unknotted).
(e) Clearly, 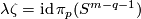 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 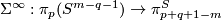 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
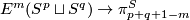 for
for 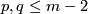 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
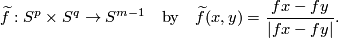
For 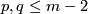 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 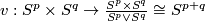 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 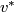 is an isomorphism for
is an isomorphism for 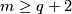 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
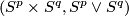 and by the existence of a retraction
and by the existence of a retraction 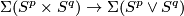 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 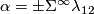 .
.
Hence 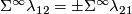 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 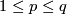 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 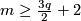 in the smooth category.
in the smooth category.
(PL) If 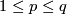 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 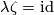 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 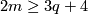 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 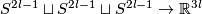 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 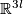 by
by 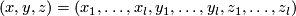 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
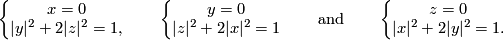
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 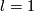 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 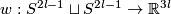 whose linking coefficient
whose linking coefficient 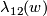 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 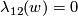 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 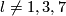 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 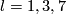 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 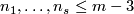 , then
, then
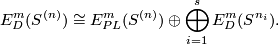
Thus 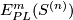 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 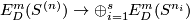 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 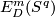 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 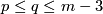 and
and 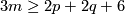 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
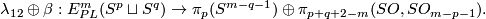
The map  and its right inverse
and its right inverse 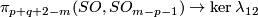 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 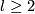 we have an isomorphism
we have an isomorphism
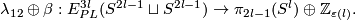
(b) When 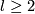 but
but 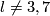 , the map
, the map
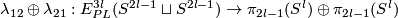
is injective and its image is 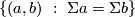 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 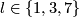 the map
the map 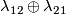 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 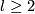 we have an isomorphism
we have an isomorphism
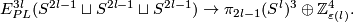
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 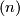 is an
is an  -tuple such that
-tuple such that 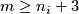 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
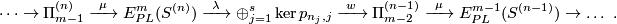
In the above sequence  -tuples
-tuples 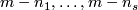 are the same for different terms. Denote
are the same for different terms. Denote 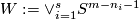 . For each
. For each 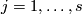 and integer
and integer 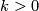 denote by
denote by 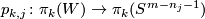 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 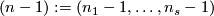 . Denote
. Denote 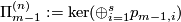 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 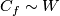 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 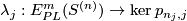 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 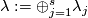 .
.
Taking the Whitehead product with the class of the identity in 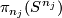 defines a homomorphism
defines a homomorphism 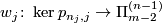 . Define
. Define 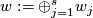 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 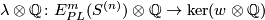 is an isomorphism.
is an isomorphism.
Part (b) follows because 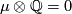 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 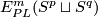 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 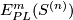 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 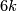 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
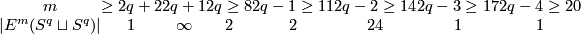
For an  -tuple
-tuple 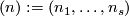 denote
denote 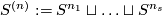 . Although
. Although 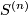 is not a manifold when
is not a manifold when 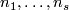 are not all equal, embeddings
are not all equal, embeddings 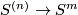 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 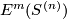 the set of embeddings
the set of embeddings 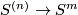 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 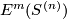 for
for 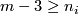 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 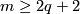 , any two embeddings
, any two embeddings  are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 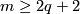 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 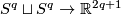 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 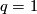 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 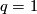 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
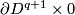 and
and 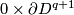 in
in 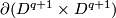 ;
;
- or given by equations:
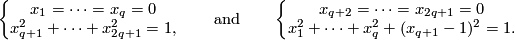
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 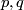 one constructs an embedding
one constructs an embedding 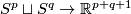 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
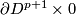 and
and 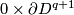 in
in 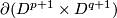 .
.
- or given by equations:
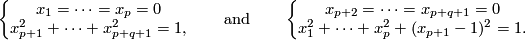
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
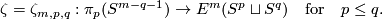
Denote by 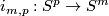 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 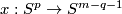 representing an element of
representing an element of 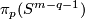 let
let
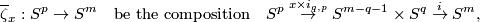
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 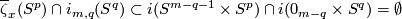 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
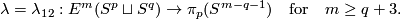
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 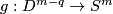 such that
such that 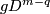 intersects
intersects 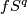 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 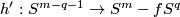 of
of  to
to 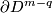 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 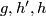 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 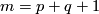 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 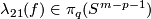 for
for 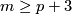 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 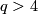 , if the restriction of
, if the restriction of  to
to 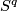 is unknotted).
is unknotted).
(e) Clearly, 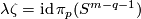 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 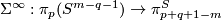 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
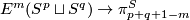 for
for 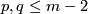 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
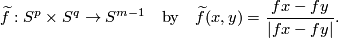
For 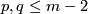 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 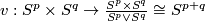 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 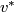 is an isomorphism for
is an isomorphism for 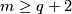 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
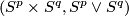 and by the existence of a retraction
and by the existence of a retraction 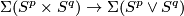 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 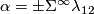 .
.
Hence 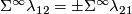 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 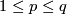 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 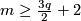 in the smooth category.
in the smooth category.
(PL) If 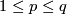 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 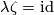 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 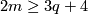 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 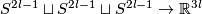 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 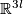 by
by 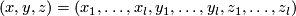 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
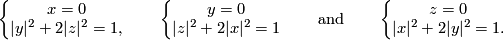
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 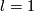 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 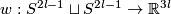 whose linking coefficient
whose linking coefficient 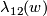 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 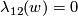 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 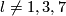 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 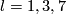 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 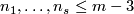 , then
, then
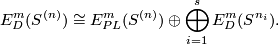
Thus 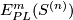 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 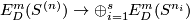 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 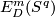 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 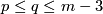 and
and 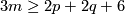 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
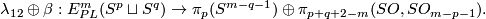
The map  and its right inverse
and its right inverse 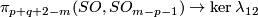 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 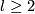 we have an isomorphism
we have an isomorphism
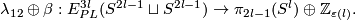
(b) When 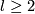 but
but  , the map
, the map
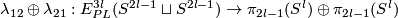
is injective and its image is 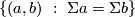 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 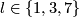 the map
the map 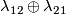 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 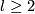 we have an isomorphism
we have an isomorphism
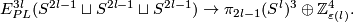
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 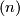 is an
is an  -tuple such that
-tuple such that 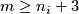 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
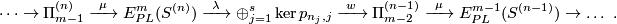
In the above sequence  -tuples
-tuples 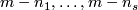 are the same for different terms. Denote
are the same for different terms. Denote 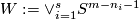 . For each
. For each 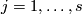 and integer
and integer 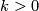 denote by
denote by 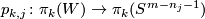 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 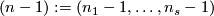 . Denote
. Denote 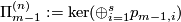 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 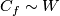 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 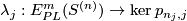 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 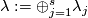 .
.
Taking the Whitehead product with the class of the identity in 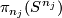 defines a homomorphism
defines a homomorphism 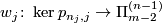 . Define
. Define 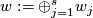 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 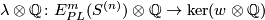 is an isomorphism.
is an isomorphism.
Part (b) follows because 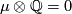 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 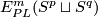 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 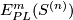 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 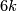 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
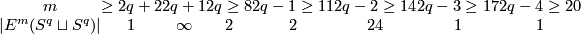
For an  -tuple
-tuple 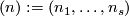 denote
denote 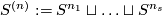 . Although
. Although 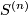 is not a manifold when
is not a manifold when 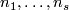 are not all equal, embeddings
are not all equal, embeddings 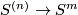 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 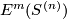 the set of embeddings
the set of embeddings 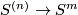 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 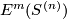 for
for 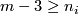 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 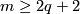 , any two embeddings
, any two embeddings 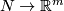 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 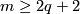 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 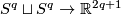 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 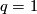 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 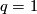 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
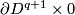 and
and 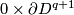 in
in 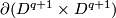 ;
;
- or given by equations:
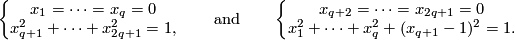
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 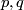 one constructs an embedding
one constructs an embedding 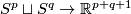 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
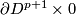 and
and 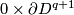 in
in 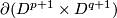 .
.
- or given by equations:
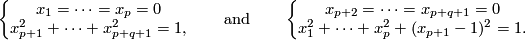
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
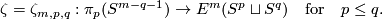
Denote by 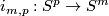 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 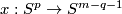 representing an element of
representing an element of 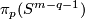 let
let
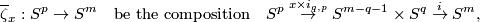
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 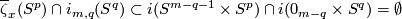 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
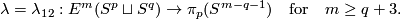
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 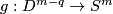 such that
such that 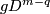 intersects
intersects 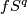 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 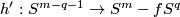 of
of  to
to  is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 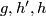 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 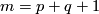 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 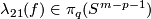 for
for 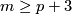 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 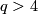 , if the restriction of
, if the restriction of  to
to 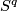 is unknotted).
is unknotted).
(e) Clearly, 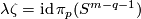 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 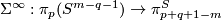 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
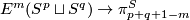 for
for 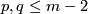 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
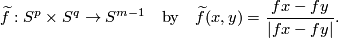
For 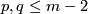 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 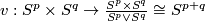 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 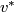 is an isomorphism for
is an isomorphism for 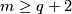 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
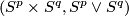 and by the existence of a retraction
and by the existence of a retraction 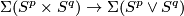 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 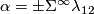 .
.
Hence 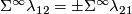 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 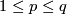 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 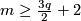 in the smooth category.
in the smooth category.
(PL) If 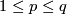 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 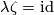 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 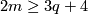 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 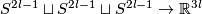 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 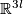 by
by 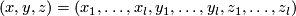 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
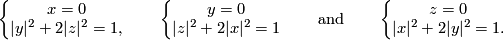
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 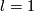 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 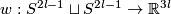 whose linking coefficient
whose linking coefficient 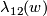 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 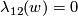 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 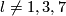 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 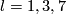 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 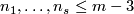 , then
, then
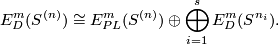
Thus 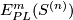 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 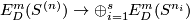 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 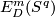 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 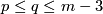 and
and 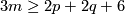 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
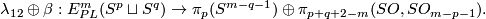
The map  and its right inverse
and its right inverse 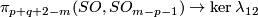 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 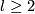 we have an isomorphism
we have an isomorphism
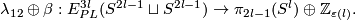
(b) When 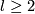 but
but 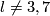 , the map
, the map
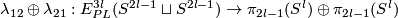
is injective and its image is 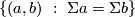 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 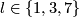 the map
the map 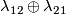 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 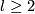 we have an isomorphism
we have an isomorphism
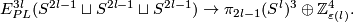
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 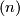 is an
is an  -tuple such that
-tuple such that 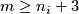 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
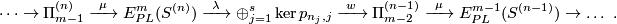
In the above sequence  -tuples
-tuples 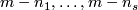 are the same for different terms. Denote
are the same for different terms. Denote 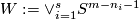 . For each
. For each 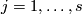 and integer
and integer 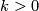 denote by
denote by 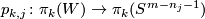 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 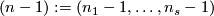 . Denote
. Denote 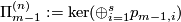 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 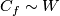 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 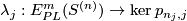 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 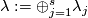 .
.
Taking the Whitehead product with the class of the identity in 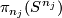 defines a homomorphism
defines a homomorphism 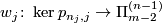 . Define
. Define 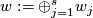 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 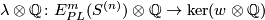 is an isomorphism.
is an isomorphism.
Part (b) follows because 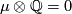 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 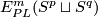 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 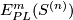 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 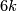 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
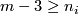 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
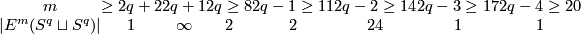
For an  -tuple
-tuple 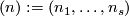 denote
denote 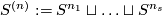 . Although
. Although 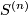 is not a manifold when
is not a manifold when 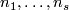 are not all equal, embeddings
are not all equal, embeddings 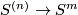 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 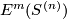 the set of embeddings
the set of embeddings 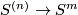 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 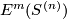 for
for 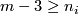 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 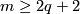 , any two embeddings
, any two embeddings 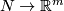 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 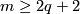 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 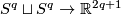 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 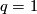 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 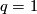 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
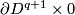 and
and 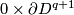 in
in 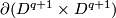 ;
;
- or given by equations:
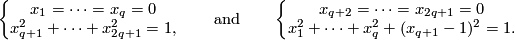
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 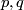 one constructs an embedding
one constructs an embedding 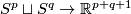 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
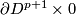 and
and 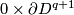 in
in 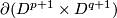 .
.
- or given by equations:
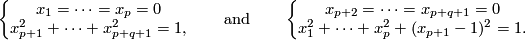
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
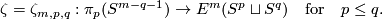
Denote by 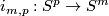 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 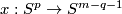 representing an element of
representing an element of  let
let
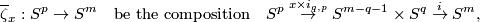
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 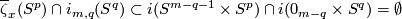 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
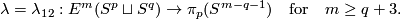
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 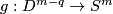 such that
such that 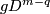 intersects
intersects 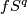 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 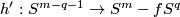 of
of  to
to 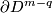 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 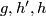 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 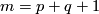 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 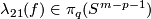 for
for 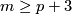 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 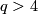 , if the restriction of
, if the restriction of  to
to 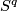 is unknotted).
is unknotted).
(e) Clearly, 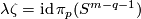 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 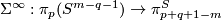 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
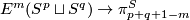 for
for 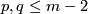 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
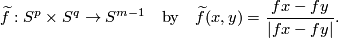
For 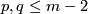 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 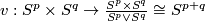 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 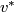 is an isomorphism for
is an isomorphism for 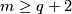 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
 and by the existence of a retraction
and by the existence of a retraction 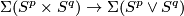 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 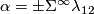 .
.
Hence 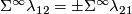 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 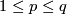 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 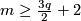 in the smooth category.
in the smooth category.
(PL) If 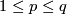 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 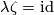 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 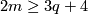 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 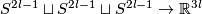 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 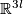 by
by 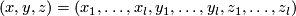 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
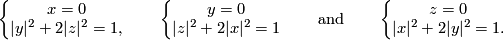
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 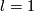 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 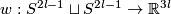 whose linking coefficient
whose linking coefficient 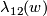 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 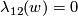 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For  the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 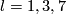 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 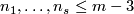 , then
, then
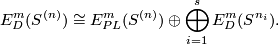
Thus 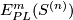 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 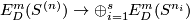 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 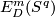 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 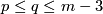 and
and 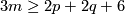 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
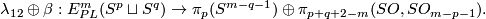
The map  and its right inverse
and its right inverse 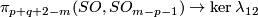 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 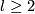 we have an isomorphism
we have an isomorphism
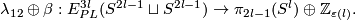
(b) When 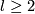 but
but 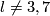 , the map
, the map
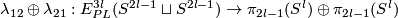
is injective and its image is 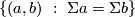 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 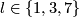 the map
the map 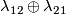 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 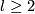 we have an isomorphism
we have an isomorphism
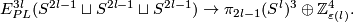
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 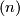 is an
is an  -tuple such that
-tuple such that 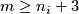 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
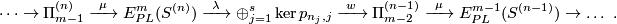
In the above sequence  -tuples
-tuples 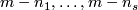 are the same for different terms. Denote
are the same for different terms. Denote 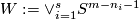 . For each
. For each 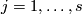 and integer
and integer 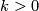 denote by
denote by 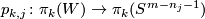 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 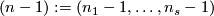 . Denote
. Denote 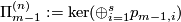 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 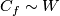 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 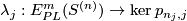 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 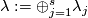 .
.
Taking the Whitehead product with the class of the identity in 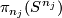 defines a homomorphism
defines a homomorphism 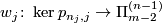 . Define
. Define 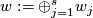 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 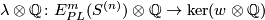 is an isomorphism.
is an isomorphism.
Part (b) follows because 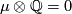 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 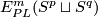 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 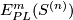 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 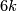 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
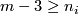 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
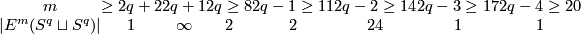
For an  -tuple
-tuple 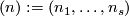 denote
denote 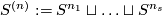 . Although
. Although 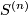 is not a manifold when
is not a manifold when 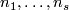 are not all equal, embeddings
are not all equal, embeddings 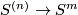 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 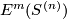 the set of embeddings
the set of embeddings 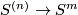 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 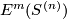 for
for 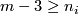 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 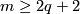 , any two embeddings
, any two embeddings 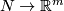 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 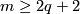 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 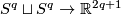 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 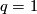 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 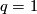 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
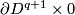 and
and 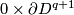 in
in 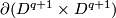 ;
;
- or given by equations:
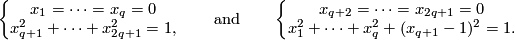
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each  one constructs an embedding
one constructs an embedding 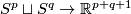 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
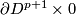 and
and 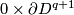 in
in 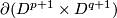 .
.
- or given by equations:
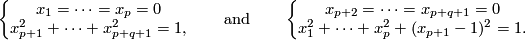
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
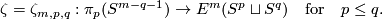
Denote by 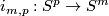 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 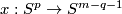 representing an element of
representing an element of 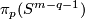 let
let
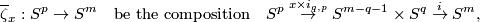
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 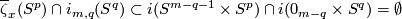 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
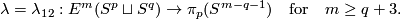
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding  such that
such that 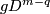 intersects
intersects 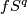 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 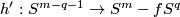 of
of  to
to 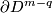 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 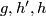 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 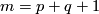 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 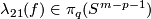 for
for 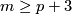 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 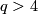 , if the restriction of
, if the restriction of  to
to 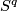 is unknotted).
is unknotted).
(e) Clearly, 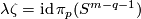 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 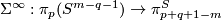 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
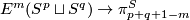 for
for 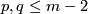 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
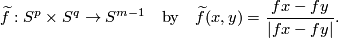
For 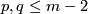 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 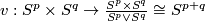 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 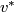 is an isomorphism for
is an isomorphism for 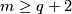 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
 and by the existence of a retraction
and by the existence of a retraction 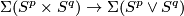 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 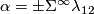 .
.
Hence 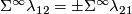 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If  , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 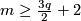 in the smooth category.
in the smooth category.
(PL) If 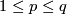 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 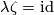 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 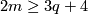 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 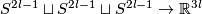 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 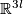 by
by 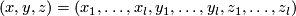 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
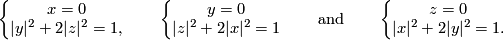
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 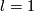 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 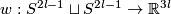 whose linking coefficient
whose linking coefficient 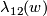 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 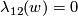 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 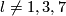 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 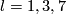 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 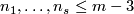 , then
, then
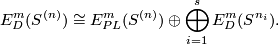
Thus 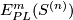 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 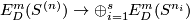 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 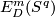 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 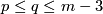 and
and 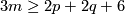 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
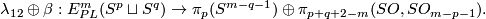
The map  and its right inverse
and its right inverse 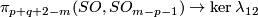 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each  we have an isomorphism
we have an isomorphism
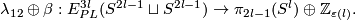
(b) When  but
but 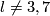 , the map
, the map
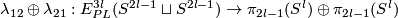
is injective and its image is 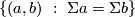 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 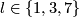 the map
the map 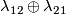 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 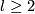 we have an isomorphism
we have an isomorphism
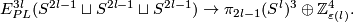
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 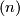 is an
is an  -tuple such that
-tuple such that  .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
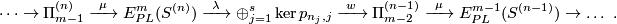
In the above sequence  -tuples
-tuples 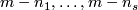 are the same for different terms. Denote
are the same for different terms. Denote 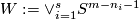 . For each
. For each  and integer
and integer  denote by
denote by 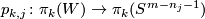 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 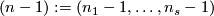 . Denote
. Denote 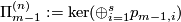 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence  . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 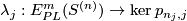 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 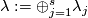 .
.
Taking the Whitehead product with the class of the identity in 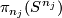 defines a homomorphism
defines a homomorphism 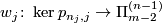 . Define
. Define 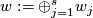 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 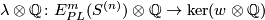 is an isomorphism.
is an isomorphism.
Part (b) follows because 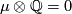 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 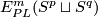 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 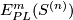 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in  -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
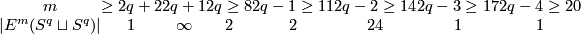
For an  -tuple
-tuple 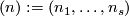 denote
denote 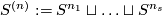 . Although
. Although 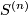 is not a manifold when
is not a manifold when  are not all equal, embeddings
are not all equal, embeddings 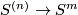 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 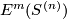 the set of embeddings
the set of embeddings 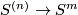 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 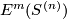 for
for 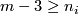 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 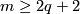 , any two embeddings
, any two embeddings 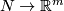 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 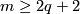 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 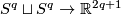 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 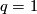 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 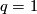 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
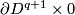 and
and 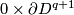 in
in 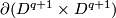 ;
;
- or given by equations:
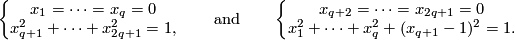
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 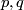 one constructs an embedding
one constructs an embedding 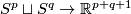 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
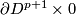 and
and 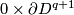 in
in 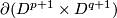 .
.
- or given by equations:
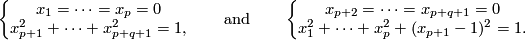
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
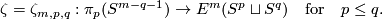
Denote by 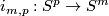 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 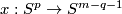 representing an element of
representing an element of 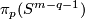 let
let
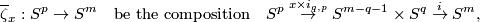
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 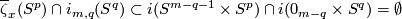 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
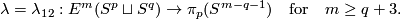
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 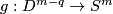 such that
such that 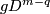 intersects
intersects 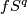 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 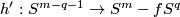 of
of  to
to 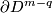 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 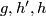 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 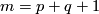 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 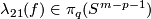 for
for 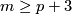 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 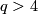 , if the restriction of
, if the restriction of  to
to 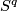 is unknotted).
is unknotted).
(e) Clearly, 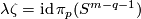 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 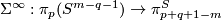 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
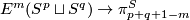 for
for 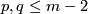 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
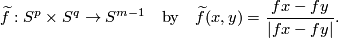
For 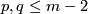 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 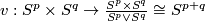 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 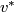 is an isomorphism for
is an isomorphism for 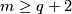 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
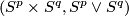 and by the existence of a retraction
and by the existence of a retraction 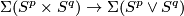 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 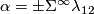 .
.
Hence 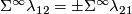 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 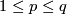 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 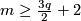 in the smooth category.
in the smooth category.
(PL) If 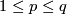 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 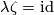 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 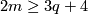 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 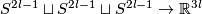 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in  by
by 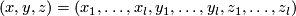 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
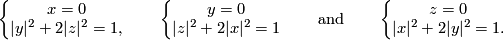
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 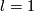 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 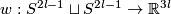 whose linking coefficient
whose linking coefficient 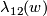 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 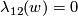 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 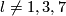 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 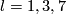 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 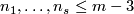 , then
, then
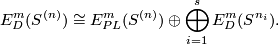
Thus 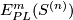 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 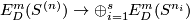 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 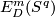 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 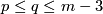 and
and 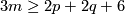 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
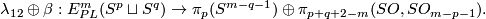
The map  and its right inverse
and its right inverse 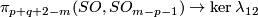 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 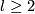 we have an isomorphism
we have an isomorphism
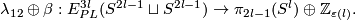
(b) When 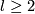 but
but 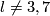 , the map
, the map
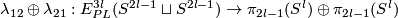
is injective and its image is 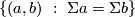 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 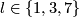 the map
the map 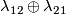 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 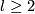 we have an isomorphism
we have an isomorphism
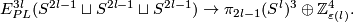
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 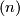 is an
is an  -tuple such that
-tuple such that 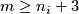 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
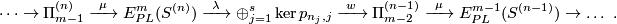
In the above sequence  -tuples
-tuples 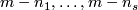 are the same for different terms. Denote
are the same for different terms. Denote 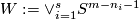 . For each
. For each  and integer
and integer 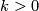 denote by
denote by 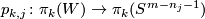 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 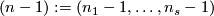 . Denote
. Denote 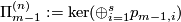 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 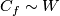 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 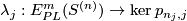 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 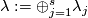 .
.
Taking the Whitehead product with the class of the identity in 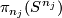 defines a homomorphism
defines a homomorphism 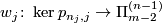 . Define
. Define 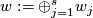 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 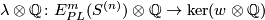 is an isomorphism.
is an isomorphism.
Part (b) follows because  [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 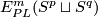 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 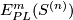 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 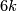 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
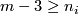 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
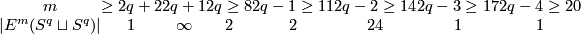
For an  -tuple
-tuple 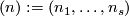 denote
denote 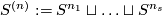 . Although
. Although 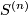 is not a manifold when
is not a manifold when 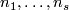 are not all equal, embeddings
are not all equal, embeddings 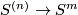 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 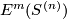 the set of embeddings
the set of embeddings 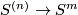 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 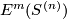 for
for 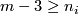 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 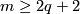 , any two embeddings
, any two embeddings 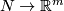 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 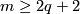 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 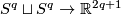 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For  the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including  ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
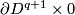 and
and 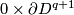 in
in 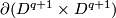 ;
;
- or given by equations:
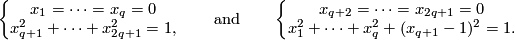
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 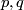 one constructs an embedding
one constructs an embedding 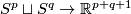 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
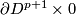 and
and 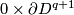 in
in 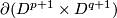 .
.
- or given by equations:
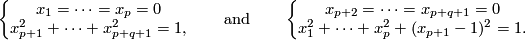
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
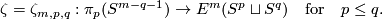
Denote by  the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 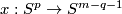 representing an element of
representing an element of 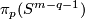 let
let
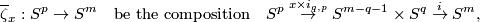
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 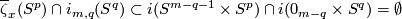 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
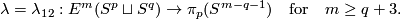
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 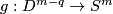 such that
such that 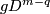 intersects
intersects 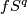 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 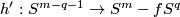 of
of  to
to  is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 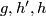 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 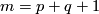 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 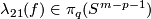 for
for 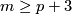 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 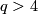 , if the restriction of
, if the restriction of  to
to 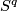 is unknotted).
is unknotted).
(e) Clearly, 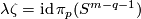 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 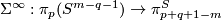 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
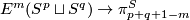 for
for  .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
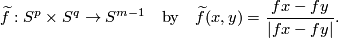
For 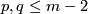 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 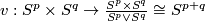 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 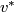 is an isomorphism for
is an isomorphism for 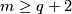 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
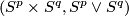 and by the existence of a retraction
and by the existence of a retraction 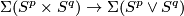 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 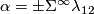 .
.
Hence 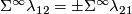 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 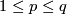 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 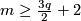 in the smooth category.
in the smooth category.
(PL) If 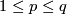 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 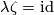 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 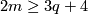 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 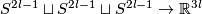 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 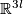 by
by 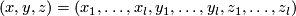 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
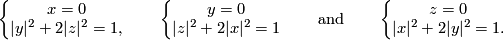
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For  this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 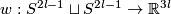 whose linking coefficient
whose linking coefficient 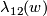 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 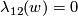 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For  the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For  the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 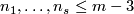 , then
, then
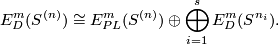
Thus  is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 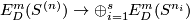 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 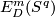 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 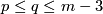 and
and 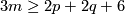 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
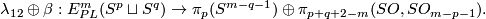
The map  and its right inverse
and its right inverse 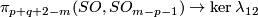 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each 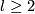 we have an isomorphism
we have an isomorphism
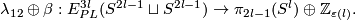
(b) When 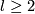 but
but 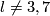 , the map
, the map
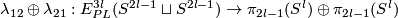
is injective and its image is 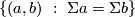 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For  the map
the map 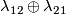 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 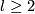 we have an isomorphism
we have an isomorphism
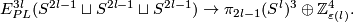
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 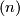 is an
is an  -tuple such that
-tuple such that 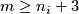 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
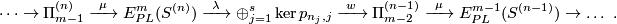
In the above sequence  -tuples
-tuples 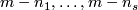 are the same for different terms. Denote
are the same for different terms. Denote 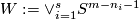 . For each
. For each 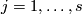 and integer
and integer 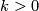 denote by
denote by 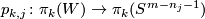 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 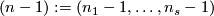 . Denote
. Denote 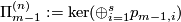 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 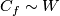 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 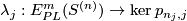 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 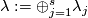 .
.
Taking the Whitehead product with the class of the identity in 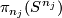 defines a homomorphism
defines a homomorphism 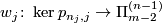 . Define
. Define 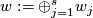 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 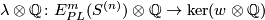 is an isomorphism.
is an isomorphism.
Part (b) follows because 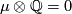 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 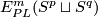 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 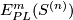 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 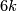 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
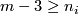 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
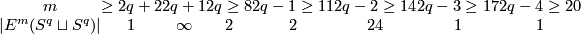
For an  -tuple
-tuple 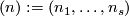 denote
denote 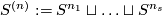 . Although
. Although 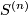 is not a manifold when
is not a manifold when 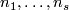 are not all equal, embeddings
are not all equal, embeddings 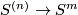 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 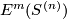 the set of embeddings
the set of embeddings 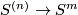 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 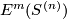 for
for 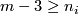 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 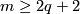 , any two embeddings
, any two embeddings 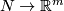 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 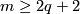 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 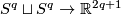 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 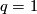 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 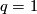 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
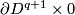 and
and 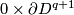 in
in 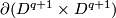 ;
;
- or given by equations:
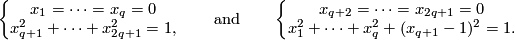
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each 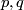 one constructs an embedding
one constructs an embedding 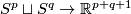 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
 and
and 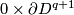 in
in 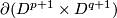 .
.
- or given by equations:
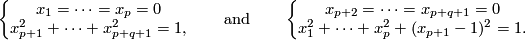
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
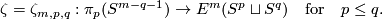
Denote by 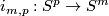 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 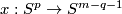 representing an element of
representing an element of  let
let
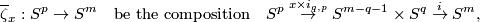
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 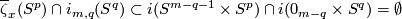 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
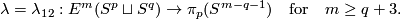
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding  such that
such that  intersects
intersects 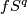 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 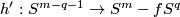 of
of  to
to  is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of  .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 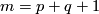 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 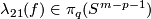 for
for 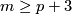 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 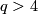 , if the restriction of
, if the restriction of  to
to 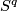 is unknotted).
is unknotted).
(e) Clearly, 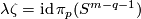 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 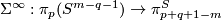 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
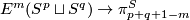 for
for 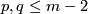 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
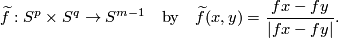
For 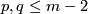 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 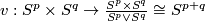 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 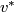 is an isomorphism for
is an isomorphism for 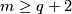 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
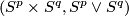 and by the existence of a retraction
and by the existence of a retraction 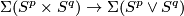 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 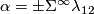 .
.
Hence 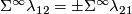 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If 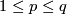 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 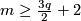 in the smooth category.
in the smooth category.
(PL) If 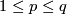 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 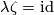 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 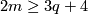 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 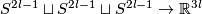 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 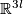 by
by 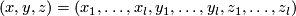 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
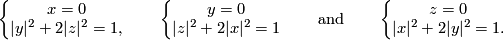
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For  this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 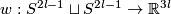 whose linking coefficient
whose linking coefficient 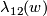 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 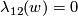 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For  the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 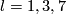 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 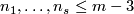 , then
, then
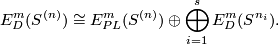
Thus 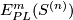 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 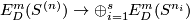 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 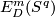 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If  and
and  , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
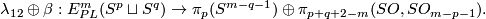
The map  and its right inverse
and its right inverse 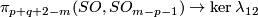 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each  we have an isomorphism
we have an isomorphism
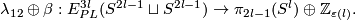
(b) When 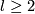 but
but 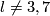 , the map
, the map
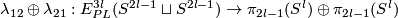
is injective and its image is 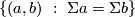 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 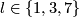 the map
the map 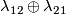 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 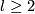 we have an isomorphism
we have an isomorphism
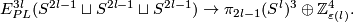
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that 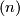 is an
is an  -tuple such that
-tuple such that 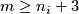 .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
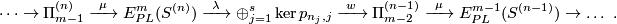
In the above sequence  -tuples
-tuples 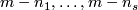 are the same for different terms. Denote
are the same for different terms. Denote 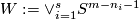 . For each
. For each  and integer
and integer  denote by
denote by 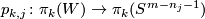 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 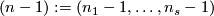 . Denote
. Denote 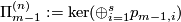 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 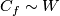 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 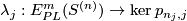 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 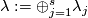 .
.
Taking the Whitehead product with the class of the identity in 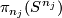 defines a homomorphism
defines a homomorphism 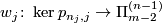 . Define
. Define 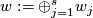 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 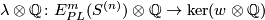 is an isomorphism.
is an isomorphism.
Part (b) follows because 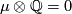 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 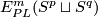 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 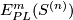 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 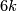 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
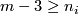 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
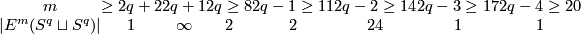
For an  -tuple
-tuple 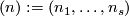 denote
denote 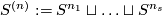 . Although
. Although 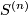 is not a manifold when
is not a manifold when 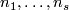 are not all equal, embeddings
are not all equal, embeddings 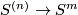 and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds. Denote by 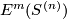 the set of embeddings
the set of embeddings 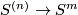 up to isotopy.
up to isotopy.
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 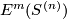 for
for 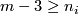 [Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
[Haefliger1966], [Haefliger1966a], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], see [Skopenkov2006, Figure 3.3].
2 Examples
Recall that for each  -manifold
-manifold  and
and 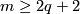 , any two embeddings
, any two embeddings 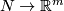 are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1].
The following example shows that the restriction 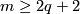 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
For each  there is an embedding
there is an embedding 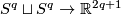 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
For 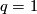 the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary
the Hopf link is shown in [Skopenkov2006, Figure 2.1.a].
For arbitrary  (including
(including 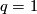 ) the image of the Hopf link is the union of two
) the image of the Hopf link is the union of two  -spheres:
-spheres:
- either
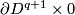 and
and 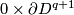 in
in 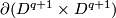 ;
;
- or given by equations:
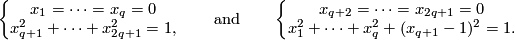
This embedding is distinguished from the standard embedding by the linking coefficient ( 3).
3).
Analogously for each  one constructs an embedding
one constructs an embedding 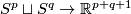 which is not isotopic to the standard embedding. The image is the union of two spheres:
which is not isotopic to the standard embedding. The image is the union of two spheres:
- either
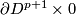 and
and 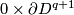 in
in 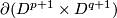 .
.
- or given by equations:
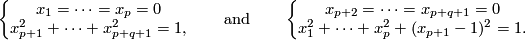
This embedding is distinguished from the standard embedding also by the linking coefficient ( 3).
3).
Definition 2.2 (The Zeeman map). We define a map
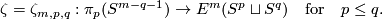
Denote by 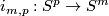 the equatorial inclusion.
For a map
the equatorial inclusion.
For a map 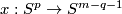 representing an element of
representing an element of 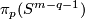 let
let
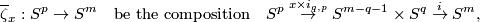
where  is the standard embedding [Skopenkov2006, Figure 3.2].
We have
is the standard embedding [Skopenkov2006, Figure 3.2].
We have 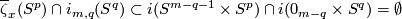 .
Let
.
Let ![\zeta[x]:=[\overline\zeta_x\sqcup i_{m,q}]](/images/math/c/4/2/c422fd90544a98b1e4657ae3f73d57f1.png) .
.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss is properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
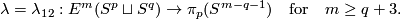
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding  such that
such that 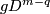 intersects
intersects 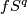 transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction
transversely at exactly one point with positive sign [Skopenkov2006, Figure 3.1].
Then the restriction 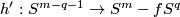 of
of  to
to 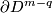 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since  , by general position the complement
, by general position the complement  is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality,  induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems  is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of  .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is indeed independent of
is indeed independent of 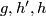 .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) For 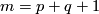 or
or  there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
there are simpler alternative definitions using homological ideas. These definitions can be generalized to the case where the components are closed orientable manifolds, cf. Remark 5.3.f of [Skopenkov2016e].
(c) Analogously one can define 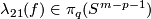 for
for 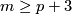 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(d) This definition extends to the case  when
when  is simply-connected
(or, equivalently for
is simply-connected
(or, equivalently for 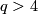 , if the restriction of
, if the restriction of  to
to 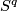 is unknotted).
is unknotted).
(e) Clearly, 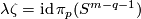 , even for
, even for  (see Definition 2.2). So
(see Definition 2.2). So  is surjective and
is surjective and  is injective.
is injective.
By the Freudenthal Suspension Theorem 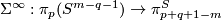 is an isomorphism for
is an isomorphism for
 .
The stabilization of the linking coefficient can be described as follows.
.
The stabilization of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
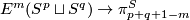 for
for 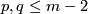 .
Take an embedding
.
Take an embedding  representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define a map [Skopenkov2006, Figure 3.1]
.
Define a map [Skopenkov2006, Figure 3.1]
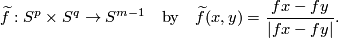
For 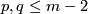 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha(f)=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/8/3/f/83faec70806146f2d1f254e1efe2193d.png)
The second isomorphism in this formula is given by the Freudenthal Suspension Theorem.
The map 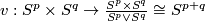 is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map
is the quotient map.
See [Skopenkov2006, Figure 3.4].
The map 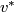 is an isomorphism for
is an isomorphism for 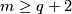 .
(For
.
(For  this follows by general position and for
this follows by general position and for  by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair
 and by the existence of a retraction
and by the existence of a retraction 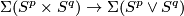 .)
.)
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 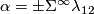 .
.
Hence 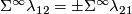 .
.
Note that  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
(D) If  , then both
, then both  and
and  are isomorphisms for
are isomorphisms for 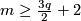 in the smooth category.
in the smooth category.
(PL) If 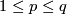 , then both
, then both  and
and  are isomorphisms for
are isomorphisms for  in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 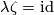 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of  ) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
) is proved in [Haefliger1962t], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components [Haefliger1966a].
Theorem 4.2.
The collection of pairwise linking coefficients is bijective for 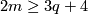 and
and  -dimensional links in
-dimensional links in  .
.
5 Examples beyond the metastable range
We present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Borromean rings example 5.1.
The embedding defined below is a non-trivial embedding 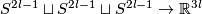 whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
whose restrictions to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t].
Denote coordinates in 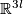 by
by 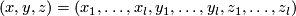 .
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
.
The (higher-dimensional) Borromean rings [Skopenkov2006, Figures 3.5 and 3.6], i
are the three spheres given by the following three systems of equations:
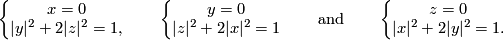
The required embedding is any embedding whose image consists of Borromean rings.
This embedding is distinguished from the standard embedding by the well-known Massey invariant [Skopenkov2017] (or because joining the three components with two tubes, i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c], yields a non-trivial knot [Haefliger1962], cf. the Haefliger Trefoil knot [Skopenkov2016t]).
For 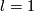 this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
this and other results of this section are parts of low-dimensional link theory and so were known well before given references.
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Whitehead link example 5.2. There is a non-trivial embedding 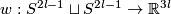 whose linking coefficient
whose linking coefficient 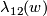 is trivial.
is trivial.
The (higher-dimensional) Whitehead link is obtained from the Borromean rings embedding by joining two components with a tube, i.e. by `linked analogue' of embedded connected sum of the components [Skopenkov2016c].
We have 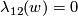 because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For
because by moving two of the three Borromean rings and self-intersecting them, we can drag the third ring apart (see details in [Skopenkov2006a]).
For 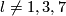 the Whitehead link is distinguished from the standard embedding by
the Whitehead link is distinguished from the standard embedding by ![\lambda_{21}(w)=[\iota_l,\iota_l]\ne0](/images/math/f/3/8/f38dc5df61caddfa7ae0c9df1fef1933.png) .
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For
.
This fact should be well-known, but I do not know a published proof except [Skopenkov2015a, Lemma 2.18].
For 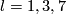 the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,
the Whitehead link is is distinguished from the standard embedding by more complicated invariants
[Skopenkov2006a], [Haefliger1962t,  3].
3].
This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
6 Classification beyond the metastable range
Theorem 6.1.
[Haefliger1966a] If 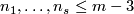 , then
, then
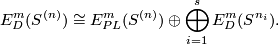
Thus 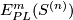 is isomorphic to the kernel of the restriction homomorphism
is isomorphic to the kernel of the restriction homomorphism 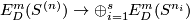 and to the group of
and to the group of  -Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups
-Brunnian links (i.e. of links whose restrictions to the components are unknotted). For some information on the groups 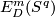 see [Skopenkov2006,
see [Skopenkov2006,  3.3].
3.3].
The Haefliger Theorem 6.2.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009]
If 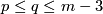 and
and 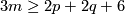 , then there is a homomorphism
, then there is a homomorphism  for which the following map is an isomorphism
for which the following map is an isomorphism
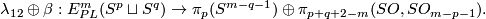
The map  and its right inverse
and its right inverse 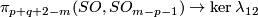 are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
are constructed in [Haefliger1966] and [Haefliger1966a], cf. [Skopenkov2009].
Remark 6.3.
(a) The Haefliger Theorem 6.2(b) implies that for each  we have an isomorphism
we have an isomorphism
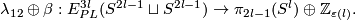
(b) When 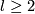 but
but 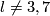 , the map
, the map
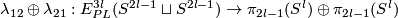
is injective and its image is 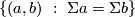 .
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
.
This is proved in [Haefliger1962t] and also follows from Theorem 6.2(b).
(c) For 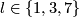 the map
the map 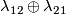 in (b) above is not injective [Haefliger1962t].
in (b) above is not injective [Haefliger1962t].
(d) [Haefliger1962t] For each 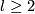 we have an isomorphism
we have an isomorphism
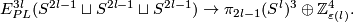
which is the sum of 3 pairwise linking coefficients, 3 pairwise  -invariants and triplewise Massey invariant.
-invariants and triplewise Massey invariant.
7 Classification in codimension 3
In this subsection we assume that  is an
is an  -tuple such that
-tuple such that  .
.
Definition 7.1 (The Haefliger link sequence). We define the following long sequence of abelian groups
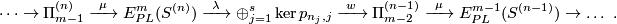
In the above sequence  -tuples
-tuples 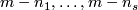 are the same for different terms. Denote
are the same for different terms. Denote 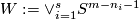 . For each
. For each  and integer
and integer  denote by
denote by 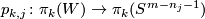 the homomorphisms induced by the projection to the
the homomorphisms induced by the projection to the  -component of the wedge. Denote
-component of the wedge. Denote 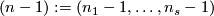 . Denote
. Denote 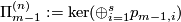 .
.
Analogously to Definition 3.1 there is a canonical homotopy equivalence 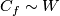 . The homotopy class of one component in the complement of the others gives then a map
. The homotopy class of one component in the complement of the others gives then a map 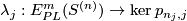 , see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define
, see details in [Haefliger1966a, 1.4] (this is a generalization of linking coefficient). Define 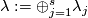 .
.
Taking the Whitehead product with the class of the identity in 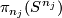 defines a homomorphism
defines a homomorphism 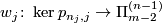 . Define
. Define 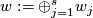 .
.
The definition of the homomorphism  is sketched in [Haefliger1966a, 1.5].
is sketched in [Haefliger1966a, 1.5].
Theorem 7.2. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) [Crowley&Ferry&Skopenkov2011] The map 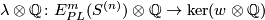 is an isomorphism.
is an isomorphism.
Part (b) follows because 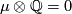 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the link Haefliger sequence splits into short exact sequences.
In [Crowley&Ferry&Skopenkov2011,  1.2,
1.2,  1.3] one can find necessary and sufficient conditions on
1.3] one can find necessary and sufficient conditions on  and
and  when
when 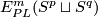 is finite, as well as an effective procedure for computing the rank of the group
is finite, as well as an effective procedure for computing the rank of the group 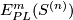 .
.
For more results related to high codimension links we refer the reader to [Skopenkov2009], [Avvakumov2016], [Skopenkov2015a,  2.5], [Skopenkov2016k].
2.5], [Skopenkov2016k].
8 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in  -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2017] A. Skopenkov, Algebraic Topology From Algorithmic Viewpoint, draft of a book.
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069