Gluck construction
(→Examples) |
|||
| Line 1: | Line 1: | ||
| − | {{Authors|Selman Akbulut}} | + | {{Authors|Selman Akbulut}}{{Definition reviewed}} |
==Definition== | ==Definition== | ||
<wikitex>; | <wikitex>; | ||
Revision as of 11:45, 15 April 2013
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:18, 16 May 2013 and the changes since publication. |
|
The user responsible for this page is Selman Akbulut. No other user may edit this page at present. |
|
This page is being independently reviewed under the supervision of the Editorial Board. |
Contents |
1 Definition
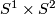 is either isotopic to identity or to the map
is either isotopic to identity or to the map 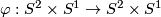 defined by
defined by 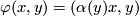 , where
, where 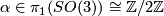 is the generator (e.g. [Wall1970b] p.232). For any smooth
is the generator (e.g. [Wall1970b] p.232). For any smooth  -manifold
-manifold  , and an imbedded 2-sphere in
, and an imbedded 2-sphere in 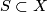 with a trivial normal bundle, the operation of removing the regular neighborhood
with a trivial normal bundle, the operation of removing the regular neighborhood 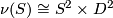 of
of 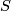 from
from  and then regluing it via the nontrivial diffeomorphism:
and then regluing it via the nontrivial diffeomorphism: 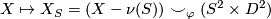
 along
along 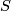 . This operation was introduced in [Gluck1962].
. This operation was introduced in [Gluck1962].
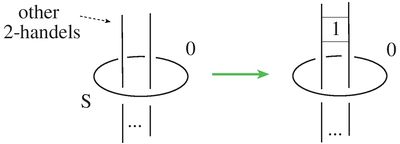
2 Examples
 is described as a handlebody, and
is described as a handlebody, and 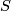 is represented by a
is represented by a  -handle attached along an unknotted circle with zero framing, then the handlebody of
-handle attached along an unknotted circle with zero framing, then the handlebody of 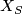 is obtained from the handlebody of
is obtained from the handlebody of  by putting one full right (or left) twist to all of the attaching framed circles of the other
by putting one full right (or left) twist to all of the attaching framed circles of the other  -handles going through this circle.
-handles going through this circle.
3 Some Results
It is known that 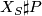 is diffeomorphic to
is diffeomorphic to 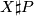 , when
, when  is a copy of
is a copy of 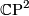 with either orientation. When
with either orientation. When 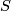 is null-homologous and
is null-homologous and  is simply connected this operation does not change the homeomorphism type of
is simply connected this operation does not change the homeomorphism type of  . It is not known whether a Gluck twisting operation can change the diffeomorphism type of any smooth orientable manifold, while it is known that this is possible in the nonorientable case ([Akbulut1988]). In many instances Gluck twisting of manifolds appear naturally, where this operation do not change their diffeomorphism types (e.g. [Gluck1962], [Akbulut1999], [Akbulut2010], [Akbulut&Yasui2012]).
. It is not known whether a Gluck twisting operation can change the diffeomorphism type of any smooth orientable manifold, while it is known that this is possible in the nonorientable case ([Akbulut1988]). In many instances Gluck twisting of manifolds appear naturally, where this operation do not change their diffeomorphism types (e.g. [Gluck1962], [Akbulut1999], [Akbulut2010], [Akbulut&Yasui2012]).
4 References
- [Akbulut&Yasui2012] S. Akbulut and K. Yasui, Gluck twisting 4-manifolds with odd intersection form, (2012). Available at the arXiv:1205.6038.
- [Akbulut1988] S. Akbulut, Constructing a fake
 -manifold by Gluck construction to a standard
-manifold by Gluck construction to a standard  -manifold, Topology 27 (1988), no.2, 239–243. MR948185 (89j:57014) Zbl 0649.57011
-manifold, Topology 27 (1988), no.2, 239–243. MR948185 (89j:57014) Zbl 0649.57011
- [Akbulut1999] S. Akbulut, Scharlemann's manifold is standard, Ann. of Math. (2) 149 (1999), no.2, 497–510. MR1689337 (2000d:57033) Zbl 0931.57016
- [Akbulut2010] S. Akbulut, Cappell-Shaneson homotopy spheres are standard, Ann. of Math. (2) 171 (2010), no.3, 2171–2175. MR2680408 (2011i:57024) Zbl 1216.57017
- [Gluck1962] H. Gluck, The embedding of two-spheres in the four-sphere, Trans. Amer. Math. Soc. 104 (1962), 308–333. MR0146807 (26 #4327) Zbl 0111.18804
- [Wall1970b] C. T. C. Wall, Surgery on compact manifolds, Academic Press, London, 1970. MR0431216 (55 #4217) Zbl 0935.57003
5 External references
The Gluck construction on the Wikipedia page about exotic spheres