Geometric 3-manifolds
From Manifold Atlas
Contents |
1 Introduction
Let a group  act on a manifold
act on a manifold  by homeomorphisms.
by homeomorphisms.
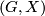 -manifold is a manifold
-manifold is a manifold  with a
with a 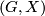 -atlas, that is, a collection
-atlas, that is, a collection 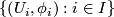 of homeomorphisms
of homeomorphisms 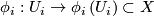
 such that all coordinate changes
such that all coordinate changes 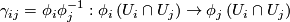
 .
Fix a basepoint
.
Fix a basepoint 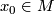 and a chart
and a chart 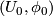 with
with 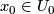 . Let
. Let 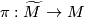 be the universal covering. These data determine the developing map
be the universal covering. These data determine the developing map 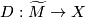
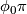 along each path, in a neighborhood of the path's endpoint.
along each path, in a neighborhood of the path's endpoint.
If we change the initial data 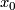 and
and 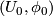 , the developing map
, the developing map 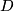 changes by composition with an element of
changes by composition with an element of  .
.
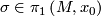 , analytic continuation along a loop representing
, analytic continuation along a loop representing 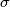 gives a chart
gives a chart 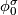 that is comparable to
that is comparable to  x_0
x_0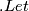 g_\sigma
g_\sigma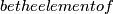 G
G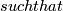 \phi_0^\sigma=g_\sigma\phi_0$. The map
\phi_0^\sigma=g_\sigma\phi_0$. The map 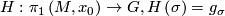
is a group homomorphism and is called the holonomy of  .
.
If we change the initial data 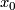 and
and 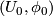 , the holonomy homomorphisms
, the holonomy homomorphisms  changes by conjugation with an element of
changes by conjugation with an element of  .
.
A 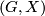 -manifold is complete if the developing map
-manifold is complete if the developing map 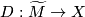 is surjective.
is surjective.
2 Construction and examples
...
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |