Geometric 3-manifolds
(→Introduction) |
|||
| Line 21: | Line 21: | ||
If we change the initial data $x_0$ and $\left(U_0,\phi_0\right)$, the developing map $D$ changes by composition with an element of $G$. | If we change the initial data $x_0$ and $\left(U_0,\phi_0\right)$, the developing map $D$ changes by composition with an element of $G$. | ||
| − | If $\sigma\in\pi_1\left(M,x_0\right)$, analytic continuation along a loop representing $\sigma$ gives a chart $\phi_0^\sigma$ that is comparable to $\phi_0, since they are both defined at $x_0$. Let $g_\sigma$ be the element of $G$ such that $\phi_0^\sigma=g_\sigma\phi_0$. The map $$H:\pi_1\left(M,x_0\right)\rightarrow G, H\left(\sigma\right)=g_\sigma$$ | + | If $\sigma\in\pi_1\left(M,x_0\right)$, analytic continuation along a loop representing $\sigma$ gives a chart $\phi_0^\sigma$ that is comparable to $\phi_0$, since they are both defined at $x_0$. Let $g_\sigma$ be the element of $G$ such that $\phi_0^\sigma=g_\sigma\phi_0$. The map $$H:\pi_1\left(M,x_0\right)\rightarrow G, H\left(\sigma\right)=g_\sigma$$ |
is a group homomorphism and is called the holonomy of $M$. | is a group homomorphism and is called the holonomy of $M$. | ||
| Line 27: | Line 27: | ||
A $\left(G,X\right)$-manifold is complete if the developing map $D:\widetilde{M}\rightarrow X$ is surjective. | A $\left(G,X\right)$-manifold is complete if the developing map $D:\widetilde{M}\rightarrow X$ is surjective. | ||
| + | |||
| + | {{cite|Thurston1997}} Section 3.4 | ||
| + | |||
| + | {{beginthm|Definition}} | ||
| + | A model geometry $\left(G,X\right)$ is a smooth manifold $X$ together with a Lie group of diffeomorphisms of $X$, such that: | ||
| + | |||
| + | a) $X$ is connected and simply connected; | ||
| + | |||
| + | b) $G$ acts transitively on $X$, with compact point stabilizers; | ||
| + | |||
| + | c) $G$ is not contained in any larger group of diffeomorphisms of $X$ with compact point stabilizers; | ||
| + | |||
| + | d) there exists at least one compact $\left(G,X\right)$-manifold. | ||
| + | {{endthm}} | ||
| + | {{cite|Thurston1997}} Definition 3.8.1 | ||
| + | |||
| + | A 3-manifold is said to be a geometric manifold if it is a $\left(G,X\right)$-manifold for a 3-dimensional model geometry $\left(G,X\right)$. | ||
</wikitex> | </wikitex> | ||
Revision as of 10:35, 8 June 2010
Contents |
1 Introduction
Let a group  act on a manifold
act on a manifold  by homeomorphisms.
by homeomorphisms.
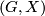 -manifold is a manifold
-manifold is a manifold Tex syntax errorwith a
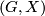 -atlas, that is, a collection
-atlas, that is, a collection 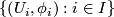 of homeomorphisms
of homeomorphisms 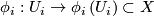
 such that all coordinate changes
such that all coordinate changes 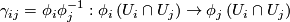
 .
Fix a basepoint
.
Fix a basepoint 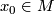 and a chart
and a chart 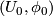 with
with 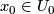 . Let
. Let 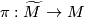 be the universal covering. These data determine the developing map
be the universal covering. These data determine the developing map 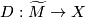
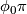 along each path, in a neighborhood of the path's endpoint.
along each path, in a neighborhood of the path's endpoint.
If we change the initial data 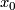 and
and 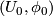 , the developing map
, the developing map 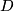 changes by composition with an element of
changes by composition with an element of  .
.
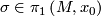 , analytic continuation along a loop representing
, analytic continuation along a loop representing 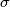 gives a chart
gives a chart 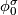 that is comparable to
that is comparable to 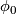 , since they are both defined at
, since they are both defined at 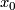 . Let
. Let 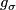 be the element of
be the element of  such that
such that 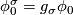 . The map
. The map 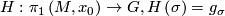
Tex syntax error.
If we change the initial data 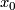 and
and 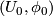 , the holonomy homomorphisms
, the holonomy homomorphisms  changes by conjugation with an element of
changes by conjugation with an element of  .
.
A 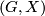 -manifold is complete if the developing map
-manifold is complete if the developing map 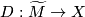 is surjective.
is surjective.
[Thurston1997] Section 3.4
Definition 1.1.
A model geometry 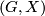 is a smooth manifold
is a smooth manifold  together with a Lie group of diffeomorphisms of
together with a Lie group of diffeomorphisms of  , such that:
, such that:
a)  is connected and simply connected;
is connected and simply connected;
b)  acts transitively on
acts transitively on  , with compact point stabilizers;
, with compact point stabilizers;
c)  is not contained in any larger group of diffeomorphisms of
is not contained in any larger group of diffeomorphisms of  with compact point stabilizers;
with compact point stabilizers;
d) there exists at least one compact 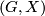 -manifold.
-manifold.
[Thurston1997] Definition 3.8.1
A 3-manifold is said to be a geometric manifold if it is a 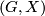 -manifold for a 3-dimensional model geometry
-manifold for a 3-dimensional model geometry 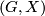 .
.
2 Construction and examples
...
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
- [Thurston1997] W. P. Thurston, Three-dimensional geometry and topology. Vol. 1, Princeton University Press, Princeton, NJ, 1997. MR1435975 (97m:57016) Zbl 0873.57001
|
This page has not been refereed. The information given here might be incomplete or provisional. |