Framed bordism
(Created page with '== Introduction == <wikitex>; The framed bordism groups $\Omega_n^{fr}$ of manifolds with a framing of the stable normal bundle (or equivalently the stable tangent bundle) are i…') |
|||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Stub}} | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
The framed bordism groups $\Omega_n^{fr}$ of manifolds with a framing of the stable normal bundle (or equivalently the stable tangent bundle) are isomorphic to the [[wikipedia:Homotopy_groups_of_spheres#Stable_and_unstable_groups|stable homotopy groups of spheres]] $\pi_n^{s}$. | The framed bordism groups $\Omega_n^{fr}$ of manifolds with a framing of the stable normal bundle (or equivalently the stable tangent bundle) are isomorphic to the [[wikipedia:Homotopy_groups_of_spheres#Stable_and_unstable_groups|stable homotopy groups of spheres]] $\pi_n^{s}$. | ||
| − | + | These groups are now completely known only in a range up to 62: They seem to be very complicated, and no general description is known. | |
(As an illustration: there is $p$-torsion in $\Omega_*^{fr}$ for all primes $p$.) | (As an illustration: there is $p$-torsion in $\Omega_*^{fr}$ for all primes $p$.) | ||
</wikitex> | </wikitex> | ||
| Line 11: | Line 12: | ||
* $\Omega_0^{fr}=\Zz$, generated by a point. | * $\Omega_0^{fr}=\Zz$, generated by a point. | ||
| − | * $\Omega_1^{fr}=\Zz_2$, generated by $S^1$. | + | * $\Omega_1^{fr}=\Zz_2$, generated by $S^1$ with the Lie group framing. |
* $\Omega_2^{fr}=\Zz_2$, | * $\Omega_2^{fr}=\Zz_2$, | ||
| − | * $\Omega_3^{fr}=\Zz_{24}$, generated by | + | * $\Omega_3^{fr}=\Zz_{24}$, generated by $S^3=SU(2)$ with the Lie group framing of |
* $\Omega_4^{fr}=\Omega_5^{fr}=0$. | * $\Omega_4^{fr}=\Omega_5^{fr}=0$. | ||
| − | See [[ | + | * $\Omega_6^{fr} = \Zz_2$, generated $S^3 \times S^3$ with the Lie group framing. |
| + | |||
| + | * $\Omega_7^{fr} \cong \Zz_{240} \cong \Zz_{16} \oplus \Zz_3 \oplus \Zz_5$, generated by $S^7$ with twisted framing defined by the generator of $\pi_7(O) \cong \Zz$. | ||
| + | |||
| + | See also: | ||
| + | *[[Wikipedia:Homotopy_groups_of_spheres#Table_of_stable_homotopy_groups|this table]] from the Wikipedia article on homotopy groups of spheres for more values. | ||
| + | *[http://www.math.cornell.edu/~hatcher/stemfigs/stems.html this table] from Allen Hatchers home page. | ||
Serre {{cite|Serre1951}} proved that $\Omega_n^{fr}$ is a finite abelian group for $n>0$. | Serre {{cite|Serre1951}} proved that $\Omega_n^{fr}$ is a finite abelian group for $n>0$. | ||
| Line 27: | Line 34: | ||
<wikitex>; | <wikitex>; | ||
Degree of a map $S^n\to S^n$. Since stably framed manifolds have stably trivial tangent bundles, all other characteristic numbers are zero. | Degree of a map $S^n\to S^n$. Since stably framed manifolds have stably trivial tangent bundles, all other characteristic numbers are zero. | ||
| − | |||
</wikitex> | </wikitex> | ||
== Classification == | == Classification == | ||
<wikitex>; | <wikitex>; | ||
| − | The case of framed bordism | + | The case of framed bordism is the original case of the [[B-Bordism#The Pontrjagin-Thom isomorphism|Pontrjagin-Thom isomorphism]], discovered by Pontryagin. The Thom spectrum $MPBO$ corresponding to the path fibration over $BO$ is homotopy equivalent to the sphere spectrum $S$ since the path space is contractible. Thus we get $$\Omega_n^{fr} \cong \pi_n(MPBO) \cong \pi_n^s.$$ |
Consequently most of the classification results use homotopy theory. | Consequently most of the classification results use homotopy theory. | ||
| Line 42: | Line 48: | ||
== Further topics == | == Further topics == | ||
| − | Kervaire invariant 1, Hopf invariant 1 problems, J-homomorphism, first $p$-torsion in degree | + | <wikitex>; |
| + | Kervaire invariant 1, Hopf invariant 1 problems, J-homomorphism, first $p$-torsion in degree. | ||
| + | </wikitex> | ||
== References == | == References == | ||
| Line 51: | Line 59: | ||
[[Category:Manifolds]] | [[Category:Manifolds]] | ||
| − | + | [[Category:Bordism]] | |
Latest revision as of 11:40, 8 July 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
The framed bordism groups 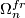 of manifolds with a framing of the stable normal bundle (or equivalently the stable tangent bundle) are isomorphic to the stable homotopy groups of spheres
of manifolds with a framing of the stable normal bundle (or equivalently the stable tangent bundle) are isomorphic to the stable homotopy groups of spheres 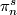 .
These groups are now completely known only in a range up to 62: They seem to be very complicated, and no general description is known.
(As an illustration: there is
.
These groups are now completely known only in a range up to 62: They seem to be very complicated, and no general description is known.
(As an illustration: there is  -torsion in
-torsion in 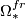 for all primes
for all primes  .)
.)
[edit] 2 Generators
-
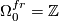 , generated by a point.
, generated by a point.
-
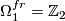 , generated by
, generated by  with the Lie group framing.
with the Lie group framing.
-
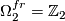 ,
,
-
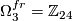 , generated by
, generated by 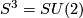 with the Lie group framing of
with the Lie group framing of
-
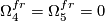 .
.
-
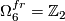 , generated
, generated 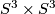 with the Lie group framing.
with the Lie group framing.
-
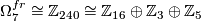 , generated by
, generated by 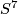 with twisted framing defined by the generator of
with twisted framing defined by the generator of 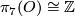 .
.
See also:
- this table from the Wikipedia article on homotopy groups of spheres for more values.
- this table from Allen Hatchers home page.
Serre [Serre1951] proved that 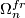 is a finite abelian group for
is a finite abelian group for 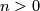 .
.
[edit] 3 Invariants
Degree of a map 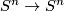 . Since stably framed manifolds have stably trivial tangent bundles, all other characteristic numbers are zero.
. Since stably framed manifolds have stably trivial tangent bundles, all other characteristic numbers are zero.
[edit] 4 Classification
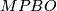 corresponding to the path fibration over
corresponding to the path fibration over 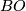 is homotopy equivalent to the sphere spectrum
is homotopy equivalent to the sphere spectrum  since the path space is contractible. Thus we get
since the path space is contractible. Thus we get 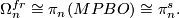
Consequently most of the classification results use homotopy theory.
Adams spectral sequence and Novikov's generalization [Ravenel1986].
Toda brackets.
Nishida [Nishida1973] proved that in the ring 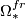 all elements of positive degree are nilpotent.
all elements of positive degree are nilpotent.
[edit] 5 Further topics
Kervaire invariant 1, Hopf invariant 1 problems, J-homomorphism, first  -torsion in degree.
-torsion in degree.
[edit] 6 References
- [Nishida1973] G. Nishida, The nilpotency of elements of the stable homotopy groups of spheres, J. Math. Soc. Japan 25 (1973), 707–732. MR0341485 (49 #6236) Zbl 0316.55014
- [Ravenel1986] D. C. Ravenel, Complex cobordism and stable homotopy groups of spheres, Academic Press Inc., Orlando, FL, 1986. MR860042 (87j:55003) Zbl 1073.55001
- [Serre1951] J. Serre, Homologie singulière des espaces fibrès. Applications, Ann. of Math. (2) 54 (1951), 425–505. MR0045386 (13,574g) Zbl 0045.26003