Foliations
(→Bundles) |
(→Suspensions) |
||
| Line 36: | Line 36: | ||
<wikitex>; | <wikitex>; | ||
A flat bundle has a foliation by fibres and it also has a foliation transverse to the fibers, whose leaves are $$L_f:= | A flat bundle has a foliation by fibres and it also has a foliation transverse to the fibers, whose leaves are $$L_f:= | ||
| − | \left\{p\left(\tilde{b},f\right): \tilde{b}\in\widetilde{B}\right\}\mbox{ | + | \left\{p\left(\tilde{b},f\right): \tilde{b}\in\widetilde{B}\right\}\ \mbox{ for }\ f\in F,$$ |
where $p:\widetilde{B}\times F\rightarrow M$ is the canonical projection. This foliation is called the suspension of the representation $\rho:\pi_1B\rightarrow \Homeo\left(F\right)$. | where $p:\widetilde{B}\times F\rightarrow M$ is the canonical projection. This foliation is called the suspension of the representation $\rho:\pi_1B\rightarrow \Homeo\left(F\right)$. | ||
Revision as of 13:41, 20 September 2012
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
 be an
be an  -manifold, possibly with boundary, and let
-manifold, possibly with boundary, and let 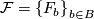 be a decomposition of
be a decomposition of  into connected, topologically immersed submanifolds of dimension
into connected, topologically immersed submanifolds of dimension  .
. 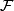 is said to be a codimension
is said to be a codimension  (smooth) foliation of
(smooth) foliation of  if
if  admits an (smooth) atlas
admits an (smooth) atlas 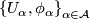 of foliated charts, that is (diffeomorphisms) homeomorphisms
of foliated charts, that is (diffeomorphisms) homeomorphisms 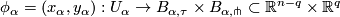
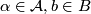 the intersection
the intersection 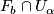 is a union of plaques
is a union of plaques 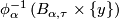 .
.
The leaves of  are the immersed submanifolds
are the immersed submanifolds 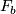 . Each
. Each 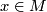 belongs to a unique leaf. The foliation
belongs to a unique leaf. The foliation  determines its tangential plane field
determines its tangential plane field 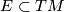 by
by 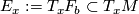 if
if 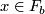 .
.
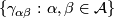 of the atlas is given by
of the atlas is given by 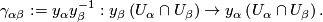
A smooth foliation 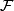 is said to be transversely orientable if
is said to be transversely orientable if 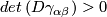 everywhere.
everywhere.
If  is a smooth, transversely orientable codimension
is a smooth, transversely orientable codimension  foliation and
foliation and  its tangential plane field, then there is a nonsingular
its tangential plane field, then there is a nonsingular  -form
-form 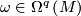 such that, for each
such that, for each 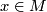 ,
,
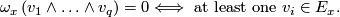
This implies that 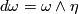 for some
for some 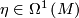 .
.
The space of leaves is 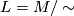 with the quotient topology, where
with the quotient topology, where 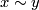 if and only if
if and only if  and
and  belong to the same leaf of
belong to the same leaf of  .
.
2 Construction and examples
2.1 Bundles
The most trivial examples of foliations are products 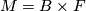 , foliated by the leaves
, foliated by the leaves 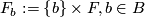 . (Another foliation of
. (Another foliation of  is given by
is given by 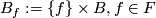 .)
.)
A more general class are flat  -bundles with
-bundles with 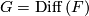 or
or  for a (smooth or topological) manifold
for a (smooth or topological) manifold  . Given a representation
. Given a representation 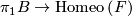 , the flat
, the flat 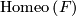 -bundle with monodromy
-bundle with monodromy 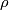 is given as
is given as 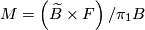 , where
, where 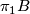 acts on the universal cober
acts on the universal cober 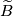 by deck transformations and on
by deck transformations and on  by means of the representation
by means of the representation 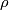 . (
. ( is a flat
is a flat 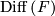 -bundle if
-bundle if 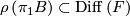 .)
.)
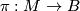
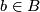 has an open neighborhood
has an open neighborhood  such that there is a homeomorphism (diffeomorphism)
such that there is a homeomorphism (diffeomorphism) 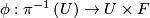 making the following diagram (with
making the following diagram (with 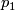 projection to the first factor) commutative:
projection to the first factor) commutative:
![\displaystyle \begin{xy} \xymatrix{ \pi^{-1}\left(U\right)\ar[d]^\pi\ar[r]^\phi &U\times F\ar[d]^{p_1}\\ U\ar[r]^{id}&U} \end{xy}](/images/math/7/2/5/72500c17d10d6bf99f9c071ac752f9d6.png)
The fiber bundle yields a foliation by fibers 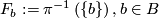 . Its space of leaves
. Its space of leaves  is (diffeomeorphic) homeomorphic to
is (diffeomeorphic) homeomorphic to  , in particular
, in particular  is a Hausdorff manifold.
is a Hausdorff manifold.
2.2 Suspensions
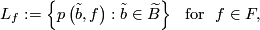
where 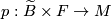 is the canonical projection. This foliation is called the suspension of the representation
is the canonical projection. This foliation is called the suspension of the representation 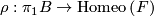 .
.
In particular, if 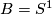 and
and 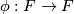 is a homeomorphism of
is a homeomorphism of  , then the suspension foliation of
, then the suspension foliation of 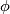 is defined to be the suspension foliation of the representation
is defined to be the suspension foliation of the representation  given by
given by 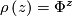 . Its space of leaves is
. Its space of leaves is 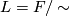 , where
, where 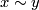 if
if 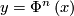 for some
for some 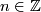 .
.
The simplest examples of suspensions are the Kronecker foliations 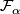 of the 2-torus, that is the suspension foliation of the rotation
of the 2-torus, that is the suspension foliation of the rotation 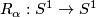 by angle
by angle 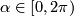 .
If
.
If  is a rational multiple of
is a rational multiple of 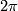 , then the leaves of
, then the leaves of 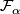 are compact. If
are compact. If  is an irrational multiple of
is an irrational multiple of 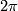 , then the leaves of
, then the leaves of 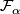 are dense on the 2-torus.
are dense on the 2-torus.
2.3 Submersions
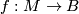
 is foliated by the preimages
is foliated by the preimages 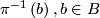 . This includes the case of fiber bundles.
. This includes the case of fiber bundles.
An example of a submersion, which is not a fiber bundle, is given by
![\displaystyle f:\left[-1,1\right]\times {\mathbb R}\rightarrow{\mathbb R}](/images/math/0/5/2/052fdc10e3d29facd86cb6b6e41e53de.png)
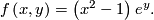
![\left[-1,1\right]\times{\mathbb R}](/images/math/5/e/0/5e00477f106f9f9bfc1dcd3bfb0c4693.png) which is invariant under the
which is invariant under the 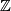 -actions given by
-actions given by 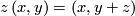
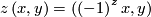
for ![\left(x,y\right)\in\left[-1,1\right]\times{\mathbb R}, z\in{\mathbb Z}](/images/math/e/c/1/ec1378db59bcd94449abc3a736c7e8d2.png) . The induced foliations of
. The induced foliations of ![{\mathbb Z}\backslash \left(\left[-1,1\right]\times{\mathbb R}\right)](/images/math/0/1/e/01ee19ac50fc1824419d5eb447938895.png) are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliaton (of the Möbius band). Their leaf spaces are not Hausdorff.
are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliaton (of the Möbius band). Their leaf spaces are not Hausdorff.
2.4 Reeb foliations
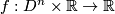
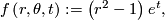
![\left(r,\theta\right)\in \left[0,1\right]\times S^{n-1}](/images/math/3/c/b/3cb41268dbbd7e42abfb3366f15c615a.png) are cylindrical coordinates on
are cylindrical coordinates on 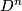 . This submersion yields a foliation of
. This submersion yields a foliation of 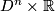 which is invariant under the
which is invariant under the 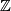 -actions given by
-actions given by 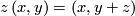
for 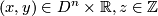 . The induced foliation of
. The induced foliation of 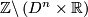 is called the n-dimensional Reeb foliation. Its leaf space is not Hausdorff.
is called the n-dimensional Reeb foliation. Its leaf space is not Hausdorff.
2.5 Taut foliations
A codimension one foliation  of
of  is taut if for every leaf
is taut if for every leaf  of
of  there is a circle transverse to
there is a circle transverse to  which intersects
which intersects  .
.
Theorem 2.1 (Rummler, Sullivan).
The following conditions are equivalent for transversely orientable codimension one foliations 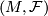 of closed, orientable, smooth manifolds
of closed, orientable, smooth manifolds  :
:
a)  is taut;
is taut;
b) there is a flow transverse to  which preserves some volume form on
which preserves some volume form on  ;
;
 for which the leaves of
for which the leaves of  are least area surfaces.
are least area surfaces.
2.6 Constructing new foliations from old ones
2.6.1 Pullbacks
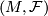 is a foliated manifold of codimension
is a foliated manifold of codimension  and
and 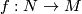 is a smooth manifold transverse to
is a smooth manifold transverse to  , then
, then  is foliated by connected components of
is foliated by connected components of 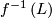 as
as  ranges over the leaves of
ranges over the leaves of  .
. [Candel&Conlon2000], Theorem 3.2.2
2.6.2 Glueing
Let 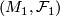 and
and 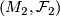 be
be  -manifolds with foliations of the same codimension. Assume there is a homeomorphism
-manifolds with foliations of the same codimension. Assume there is a homeomorphism 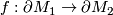 .
If either both foliations are tangent or both foliations are transverse to the boundaries of
.
If either both foliations are tangent or both foliations are transverse to the boundaries of  and
and 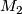 , then they can be glued to a foliation on
, then they can be glued to a foliation on 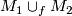 . This is called the tangential resp. the transversal glueing of
. This is called the tangential resp. the transversal glueing of 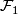 and
and 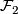 .
.
2.6.3 Turbulization
Let 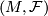 be a transversely orientable codimension 1 foliation, and let
be a transversely orientable codimension 1 foliation, and let 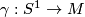 be an embedding transverse to
be an embedding transverse to  .
.
Define a foliation 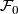 on a small neighborhood
on a small neighborhood 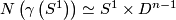 by
by
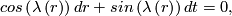
![\left(t,r,\theta\right)\in S^1\times \left[0,1\right]\times S^{n-2}\rightarrow S^1\times D^{n-1}](/images/math/3/f/b/3fbf98245ae610938482eae5495cd808.png) , and
, and ![\lambda:\left[0,1\right]\rightarrow\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](/images/math/8/c/b/8cb553a8127f8d2b0f60d91295f357f5.png) is a smooth function with
is a smooth function with ![\displaystyle \lambda\left(0\right)=-\frac{\pi}{2}, \lambda\mid_{\left[1-\epsilon,1\right]}\equiv \frac{\pi}{2}\mbox{\ for\ some\ }\epsilon>0, \lambda^\prime\left(t\right)>0\mbox{\ for\ all\ }t\in\left(0,1-\epsilon\right), \lambda^{\left(k\right)}\left(0\right)=0\mbox{\ for\ all\ }k\ge 1.](/images/math/a/1/d/a1ddc238831322e1d4b47eccae92edd7.png)
The foliations 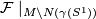 and
and 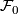 agree on a neighborhood of the boundary of
agree on a neighborhood of the boundary of 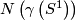 . The result of glueing these foliations is called the turbulization
. The result of glueing these foliations is called the turbulization 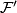 of
of  .
.
3 Invariants
3.1 Holonomy
Let 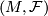 be a foliation and
be a foliation and  a leaf. For a path
a leaf. For a path ![\gamma:\left[0,1\right]\rightarrow L](/images/math/9/9/7/997482171295cc82253b2ea2976119b1.png) contained in the intersection of the leaf
contained in the intersection of the leaf  with
with
 , and two transversals
, and two transversals 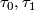 to
to 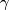 at the endpoints, the product structure of the foliation chart determines a homeomorphism
at the endpoints, the product structure of the foliation chart determines a homeomorphism 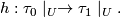
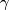 is covered by foliation charts
is covered by foliation charts 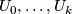 , then one obtains a sequence of homeomorphisms
, then one obtains a sequence of homeomorphisms 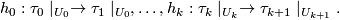
The composition yields a well-defined map  from the germ of
from the germ of 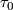 at
at 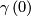 to the germ of
to the germ of 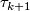 at
at 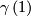 , the so-called holonomy transport. The holonomy transport only depends on the relative homotopy class of
, the so-called holonomy transport. The holonomy transport only depends on the relative homotopy class of 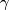 .
.
Lemma 3.1.
Let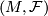 be a foliation,
be a foliation,  a leaf,
a leaf, 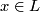 and
and  a transversal at
a transversal at  . Holonomy transport defines a homomorphism
. Holonomy transport defines a homomorphism 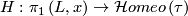
 .
.
Corollary 3.2 (Reeb).
Let 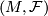 be a transversely orientable codimension one foliation of a 3-manifold such that some leaf
be a transversely orientable codimension one foliation of a 3-manifold such that some leaf  is homeomorphic to
is homeomorphic to  . Then
. Then 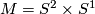 and
and  is the product foliation by spheres.
is the product foliation by spheres.
[Calegari2007] Theorem 4.5
3.2 Godbillon-Vey invariant
If  is a smooth, transversely orientable codimension
is a smooth, transversely orientable codimension  foliation of a manifold
foliation of a manifold  , then its tangential plane field
, then its tangential plane field  is defined by a nonsingular
is defined by a nonsingular  -form
-form 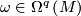 and
and 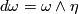 for some
for some 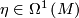 . The Godbillon-Vey invariant of
. The Godbillon-Vey invariant of  is defined as
is defined as
![\displaystyle gv\left({\mathcal{F}}\right):=\left[\eta\wedge\left(d\eta\right)^q\right]\in H^{2q+1}_{dR}\left(M\right).](/images/math/3/b/2/3b2c7cfde68606b7d423ffdf55998ae0.png)
The Godbillion-Vey invariant is related to resilience of leaves. A leaf is said to be resilient if it is not properly embedded and its holonomy is not trivial.
Theorem 3.3 (Duminy).
If 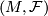 is a foliation of codimension one and no leaf is resilient, then
is a foliation of codimension one and no leaf is resilient, then 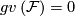 .
.
4 Classification
4.1 Codimension one foliations
4.1.1 Existence
Theorem 4.1.
A closed smooth manifold 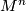 has a smooth codimension one foliation if and only if
has a smooth codimension one foliation if and only if 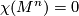 , where
, where 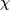 denotes the Euler characteristic.
denotes the Euler characteristic.
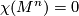 , then every
, then every  -plane field
-plane field 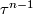 on
on 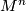 is homotopic to the tangent plane field of a smooth codimension one foliation.
is homotopic to the tangent plane field of a smooth codimension one foliation.4.1.2 Foliations of surfaces
If 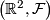 is a codimension one foliation of the plane
is a codimension one foliation of the plane 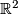 , then its space of leaves is a (possibly non-Hausdorff) simply connected 1-manifold
, then its space of leaves is a (possibly non-Hausdorff) simply connected 1-manifold  . This provides a 1-1-correspondence between foliations of
. This provides a 1-1-correspondence between foliations of 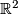 and simply connected 1-manifolds.
and simply connected 1-manifolds.
Codimension one foliations on compact surfaces 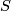 exist only if
exist only if 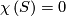 , that is on the Torus, the Klein bottle, the annulus and the Möbius band.
, that is on the Torus, the Klein bottle, the annulus and the Möbius band.
A foliation 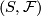 is said to contain a Reeb component resp. a non-orientable Reeb component if the restriction of
is said to contain a Reeb component resp. a non-orientable Reeb component if the restriction of 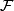 to some subsurface
to some subsurface 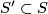 is a Reeb foliation resp. a non-orientable Reeb foliation. (This implies that
is a Reeb foliation resp. a non-orientable Reeb foliation. (This implies that 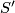 is an annulus resp. a Möbius band.)
is an annulus resp. a Möbius band.)
Theorem 4.2.
a) Let 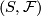 be a foliated torus or Klein bottle. Then we have one of the two exclusive situations:
be a foliated torus or Klein bottle. Then we have one of the two exclusive situations:
(1)  is the suspension of a homeomorphism
is the suspension of a homeomorphism 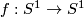 or
or
(2)  contains a Reeb component (orientable or not).
contains a Reeb component (orientable or not).
b) Every foliation of the annulus 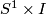 tangent to the boundary is obtained by glueing together a finite number of Reeb components and a finite number of suspensions
tangent to the boundary is obtained by glueing together a finite number of Reeb components and a finite number of suspensions
c) Every foliation of the Möbius band tangent to the boundary is one of the following three possibly glued together with a foliation on 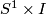 :
:
(1) the non-orientable Reeb component
(2) the orientable Reeb component identified on one boundary circle by means of a fixed point free involution
(3) the suspension of an orientation-reversing homeomorpism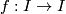 .
.[Hector&Hirsch1981], Theorem 4.2.15 and Proposition 4.3.2
4.1.3 Foliations of 3-manifolds
 admits a foliation
admits a foliation  without Reeb components, then
without Reeb components, then 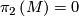 , every leaf of
, every leaf of  is incompressible, and every transverse loop is essential in
is incompressible, and every transverse loop is essential in 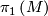 .
. [Calegari2007] Theorem 4.37
A taut foliation has no Reeb component. If  is an atoroidal 3-manifold, then, conversely, every foliation without Reeb components is taut.
is an atoroidal 3-manifold, then, conversely, every foliation without Reeb components is taut.
 is a taut foliation of a 3-manifold
is a taut foliation of a 3-manifold  not finitely covered by
not finitely covered by 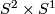 , then the universal covering
, then the universal covering 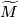 is homeomorphic to
is homeomorphic to 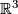 and the pull-back foliation
and the pull-back foliation 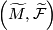 is homeomorphic to a product foliation
is homeomorphic to a product foliation 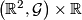 , where
, where 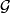 is a foliation of
is a foliation of 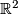 by lines.
by lines.[Calegari2007] Theorem 4.38
In particular, a taut foliation of a 3-manifold  yields an action of
yields an action of 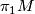 on a (possibly non-Hausdorff) simply connected 1-manifold
on a (possibly non-Hausdorff) simply connected 1-manifold  , the space of leaves of
, the space of leaves of 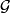 .
.
Theorem 4.5 (Gabai). Let  be a closed, irreducible 3-manifold.
be a closed, irreducible 3-manifold.
a) If 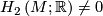 , then
, then  admits a taut foliation.
admits a taut foliation.
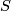 is a surface which minimizes the Thurston norm in its homology class
is a surface which minimizes the Thurston norm in its homology class ![\left[S\right]\in H_2\left(M;{\mathbb R}\right)](/images/math/8/7/5/875ecfe79ac320198542724d4cacb126.png) , then
, then  admits a taut foliaton for which
admits a taut foliaton for which 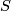 is a leaf.
is a leaf.1 Codimension two foliations
1.1  -foliations of 3-manifolds
-foliations of 3-manifolds
Example 4.7.
a) For every rational number 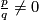 there exists a foliaton of
there exists a foliaton of 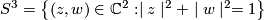 by circles such that restriction to the standard embedded torus
by circles such that restriction to the standard embedded torus 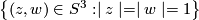 is the suspension foliation of
is the suspension foliation of 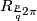 .
.
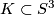 admits a foliation by circles if and only if
admits a foliation by circles if and only if  is a torus knot.
is a torus knot. admits a foliation by circles, then any 3-manifold obtained by removing finitely many points from
admits a foliation by circles, then any 3-manifold obtained by removing finitely many points from  admits a (not necessarily smooth) foliation by circles.
admits a (not necessarily smooth) foliation by circles.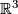 admits a foliation by circles.
admits a foliation by circles.2 Further discussion
...
5 References
- [Calegari2007] D. Calegari, Foliations and the geometry of 3-manifolds., Oxford Mathematical Monographs; Oxford Science Publications. Oxford University Press, Oxford, 2007. MR2327361 (2008k:57048) Zbl 1118.57002
- [Candel&Conlon2000] A. Candel and L. Conlon, Foliations. I, American Mathematical Society, Providence, RI, 2000. MR1732868 (2002f:57058) Zbl 0936.57001
- [Hector&Hirsch1981] G. Hector and U. Hirsch, Introduction to the geometry of foliations. Part A, Friedr. Vieweg \& Sohn, Braunschweig, 1981. MR639738 (83d:57019) Zbl 0628.57001
- [Thurston1976] W. P. Thurston, Existence of codimension-one foliations, Ann. of Math. (2) 104 (1976), no.2, 249–268. MR0425985 (54 #13934) Zbl 0347.57014
|
This page has not been refereed. The information given here might be incomplete or provisional. |

