Foliations
(→Pullbacks) |
(→Foliations of surfaces) |
||
| Line 81: | Line 81: | ||
==== Foliations of surfaces ==== | ==== Foliations of surfaces ==== | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | Codimension one foliations exist only on surfaces $S$ with $\chi\left(S\right)=0$, that is on the Torus, the Klein bottle, the annulus and the M\"obius band. |
| + | |||
| + | {{beginthm|Theorem}} | ||
| + | a) Let $\left(S,{\mathcal{F}}\right) be a foliated torus or Klein bottle. Then we have one of the two exclusive situations: | ||
| + | (1) $\mathcal{F}$ is the foliation by fibres of a flat $Homeo\left(S^1\right)$-bundle or | ||
| + | (2) $\mathcal{F}$ contains a Reeb component (orientable or not). | ||
| + | b) Every foliation of the annulus $S^1\times I$ tangent to the boundary is obtained by glueing together a finite number of Reeb components and a finite number of flat $Homeo\left(I\right)$-bundles | ||
| + | c) Every foliation of the Möbius band tangent to the boundary is one of the fllowing three possibly glued together with a foliation on $S^1\times I$: | ||
| + | (1) the non-orientable Reeb component | ||
| + | (2) the orientable Reeb component identified on one boundary circle by means of a fixed point free involution | ||
| + | (3) a flat $Homeo\left(I\right)$-bundle with monodromy $\rho:{\mathbb Z}\rightarrow Homeo\left(I\right)$ such that $\rho\left(1\right)$ is orientation-reversing.{{endthm}} | ||
| + | |||
</wikitex> | </wikitex> | ||
Revision as of 15:52, 7 June 2010
Contents |
1 Introduction
 be an
be an  -manifold, possibly with boundary, and let
-manifold, possibly with boundary, and let 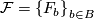 be a decomposition of
be a decomposition of  into connected, topologically immersed submanifolds of dimension
into connected, topologically immersed submanifolds of dimension  .
. 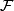 is said to be a codimension
is said to be a codimension  foliation of
foliation of  if
if  admits an atlas
admits an atlas 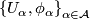 of foliated charts, that is charts (diffeomorphisms)
of foliated charts, that is charts (diffeomorphisms) 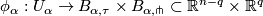
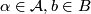 the intersection
the intersection 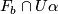 is a union of plaques
is a union of plaques 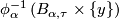 .
.
2 Construction and examples
2.1 Bundles
The most trivial examples of foliations are products 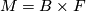 , foliated by the leaves
, foliated by the leaves 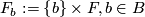 . (Another foliation of
. (Another foliation of  is given by
is given by 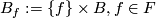 .)
.)
A more general class are flat 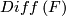 -bundles. Given a representation
-bundles. Given a representation 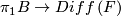 , the flat
, the flat 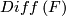 -bundle with monodromy
-bundle with monodromy  is given as
is given as 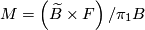 , where
, where 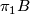 acts on the universal cober
acts on the universal cober 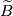 by deck transformations and on
by deck transformations and on  by means of the representation
by means of the representation  .
A flat bundle has a foliation by fibres and it also has a foliation transverse to the fibers.
.
A flat bundle has a foliation by fibres and it also has a foliation transverse to the fibers.
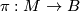
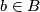 has an open neighborhood
has an open neighborhood  such that there is a diffeomorphism
such that there is a diffeomorphism 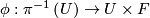 making the following diagram (with
making the following diagram (with 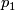 projection to the first factor) commutative:
projection to the first factor) commutative:
![\displaystyle \begin{xy} \xymatrix{ \pi^{-1}\left(U\right)\ar[d]^\pi\ar[r]^\phi &U\times F\ar[d]^{p_1}\\ U\ar[r]^{id}&U} \end{xy}](/images/math/7/2/5/72500c17d10d6bf99f9c071ac752f9d6.png)
The fiber bundle yields a foliation by fibers 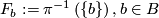 . Its leaf space is (diffeomeorphic) homeomorphic to
. Its leaf space is (diffeomeorphic) homeomorphic to  .
.
2.2 Submersions
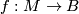
 is foliated by the preimages
is foliated by the preimages 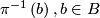 . This includes the case of fiber bundles. An example of a submersion, which is not a fiber bundle, is given by
. This includes the case of fiber bundles. An example of a submersion, which is not a fiber bundle, is given by
![\displaystyle f:\left[-1,1\right]\times {\mathbb R}\rightarrow{\mathbb R}](/images/math/0/5/2/052fdc10e3d29facd86cb6b6e41e53de.png)
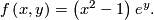
This submersion yields a foliation of ![\left[-1,1\right]\times{\mathbb R}](/images/math/5/e/0/5e00477f106f9f9bfc1dcd3bfb0c4693.png) which is invariant under the
which is invariant under the 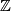 -action given by
-action given by 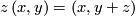 for
for ![\left(x,y\right)\in\left[[-1,1\right]\times{\mathbb R}, z\in{\mathbb Z}](/images/math/c/4/7/c47737e8bd94d6860f9fed3b291edd89.png) . The induced foliation of
. The induced foliation of ![{\mathbb Z}\backslash \left(\left[-1,1\right]\times{\mathbb R}\right)=\left[-1,1\right]\times S^1](/images/math/4/2/b/42b46b7e1e189189426195ea68f14e2f.png) is called the 2-dimensional Reeb foliation. Its leaf space is not Hausdorff.
is called the 2-dimensional Reeb foliation. Its leaf space is not Hausdorff.
2.3 Constructing new foliations from old ones
2.3.1 Pullbacks
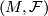 is a foliated manifold of codimension
is a foliated manifold of codimension  and
and 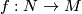 is a smooth manifold transverse to
is a smooth manifold transverse to  , then
, then  is foliated by connected components of
is foliated by connected components of 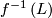 as
as  ranges over the leaves of
ranges over the leaves of  .
. 2.3.2 Glueing
Let 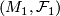 and
and 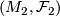 be
be  -manifolds with foliations of the same codimension. Assume there is a homeomorphism
-manifolds with foliations of the same codimension. Assume there is a homeomorphism 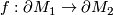 .
If either both foliations are tangent or both foliations are transverse to the boundaries of
.
If either both foliations are tangent or both foliations are transverse to the boundaries of  and
and 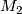 , then they can be glued to a foliation on
, then they can be glued to a foliation on 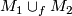 . This called the tangential resp. the transversal glueing of
. This called the tangential resp. the transversal glueing of 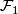 and
and 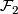 .
.
2.3.3 Turbulization
Let 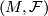 be a transversely orientable codimension 1 foliation, and let
be a transversely orientable codimension 1 foliation, and let 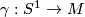 be an embedding transverse to
be an embedding transverse to  .
.
Define a foliation 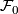 on a small neighborhood
on a small neighborhood 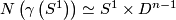 by
by
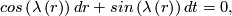
![\left(t,r,\theta\right)\in S^1\times \left[0,1\right]\times S^{n-2}\rightarrow S^1\times D^{n-1}](/images/math/3/f/b/3fbf98245ae610938482eae5495cd808.png) , and
, and ![\lambda:\left[0,1\right]\rightarrow\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](/images/math/8/c/b/8cb553a8127f8d2b0f60d91295f357f5.png) is a smooth function with
is a smooth function with ![\displaystyle \lambda\left(0\right)=-\frac{\pi}{2}, \lambda\mid_{\left[1-\epsilon,1\right]}\equiv \frac{\pi}{2}\mbox{\ for\ some\ }\epsilon>0, \lambda^\prime\left(t\right)>0\mbox{\ for\ all\ }t\in\left(0,1-\epsilon\right), \lambda^{\left(k\right)}\left(0\right)=0\mbox{\ for\ all\ }k\ge 1.](/images/math/a/1/d/a1ddc238831322e1d4b47eccae92edd7.png)
The foliations 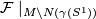 and
and 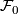 agree on a neighborhod of the boundary of
agree on a neighborhod of the boundary of 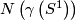 . The result of glueing these foliations is called the turbulization
. The result of glueing these foliations is called the turbulization 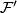 of
of  .
.
Invariants
...
3 Classification/Characterization
3.1 Codimension one foliations
A necessary condition for the existence of a codimension one foliation on a manifold  is the vanishing of the Euler characteristic
is the vanishing of the Euler characteristic 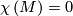 .
.
3.1.1 Foliations of surfaces
Codimension one foliations exist only on surfaces  with
with 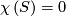 , that is on the Torus, the Klein bottle, the annulus and the M\"obius band.
, that is on the Torus, the Klein bottle, the annulus and the M\"obius band.
Theorem 5.1.
a) Let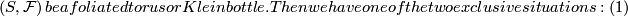 \mathcal{F}
\mathcal{F}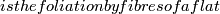 Homeo\left(S^1\right)
Homeo\left(S^1\right)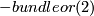 \mathcal{F}
\mathcal{F}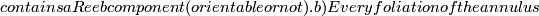 S^1\times I
S^1\times I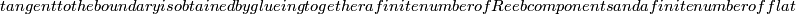 Homeo\left(I\right)
Homeo\left(I\right) S^1\times I
S^1\times I Homeo\left(I\right)
Homeo\left(I\right) \rho:{\mathbb Z}\rightarrow Homeo\left(I\right)
\rho:{\mathbb Z}\rightarrow Homeo\left(I\right) \rho\left(1\right)$ is orientation-reversing.
\rho\left(1\right)$ is orientation-reversing.
4 Further discussion
...
5 References
- [Candel&Conlon2000] A. Candel and L. Conlon, Foliations. I, American Mathematical Society, Providence, RI, 2000. MR1732868 (2002f:57058) Zbl 0936.57001
|
This page has not been refereed. The information given here might be incomplete or provisional. |