Foliation
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
This page gives the definition of the term foliation. For further information, see the page Foliations.
1.1 Foliations
 be an
be an  -manifold, possibly with boundary, and let
-manifold, possibly with boundary, and let 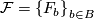 be a decomposition of
be a decomposition of  into connected, topologically immersed submanifolds of dimension
into connected, topologically immersed submanifolds of dimension  .
. 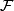 is said to be a codimension
is said to be a codimension  (smooth) foliation of
(smooth) foliation of  if
if  admits an (smooth) atlas
admits an (smooth) atlas 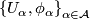 of foliated charts, that is (diffeomorphisms) homeomorphisms
of foliated charts, that is (diffeomorphisms) homeomorphisms 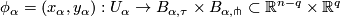
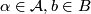 the intersection
the intersection 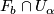 is a union of plaques
is a union of plaques 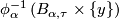 .
.
1.2 Defining differential form
If  is a smooth, transversely orientable codimension
is a smooth, transversely orientable codimension  foliation and
foliation and  its tangential plane field, then there is a nonsingular
its tangential plane field, then there is a nonsingular  -form
-form 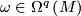 such that, for each
such that, for each 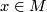 ,
,
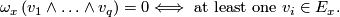
This implies that 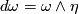 for some
for some 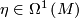 .
.
1.3 Leaves
The leaves of  are the immersed submanifolds
are the immersed submanifolds 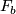 . Each
. Each 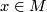 belongs to a unique leaf. The foliation
belongs to a unique leaf. The foliation  determines its tangential plane field
determines its tangential plane field 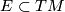 by
by 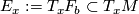 if
if 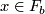 .
.
The space of leaves is 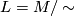 with the quotient topology, where
with the quotient topology, where 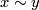 if and only if
if and only if  and
and  belong to the same leaf of
belong to the same leaf of  .
.
1.4 Holonomy Cocycle
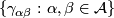 of the atlas is given by
of the atlas is given by 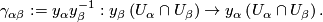
A smooth foliation 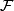 is said to be transversely orientable if
is said to be transversely orientable if 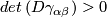 everywhere.
everywhere.
2 Special classes of foliations
2.1 Bundles
The most trivial examples of foliations are products 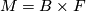 , foliated by the leaves
, foliated by the leaves 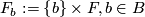 . (Another foliation of
. (Another foliation of  is given by
is given by 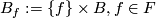 .)
.)
A more general class are flat  -bundles with
-bundles with 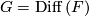 or
or  for a (smooth or topological) manifold
for a (smooth or topological) manifold  . Given a representation
. Given a representation 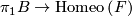 , the flat
, the flat 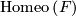 -bundle with monodromy
-bundle with monodromy  is given as
is given as 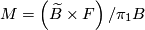 , where
, where 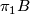 acts on the universal cober
acts on the universal cober 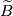 by deck transformations and on
by deck transformations and on  by means of the representation
by means of the representation  . (
. ( is a flat
is a flat 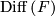 -bundle if
-bundle if 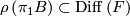 .)
.)
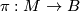
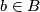 has an open neighborhood
has an open neighborhood  such that there is a homeomorphism (diffeomorphism)
such that there is a homeomorphism (diffeomorphism) 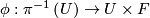 making the following diagram (with
making the following diagram (with 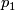 projection to the first factor) commutative:
projection to the first factor) commutative:
![\displaystyle \begin{xy} \xymatrix{ \pi^{-1}\left(U\right)\ar[d]^\pi\ar[r]^\phi &U\times F\ar[d]^{p_1}\\ U\ar[r]^{id}&U} \end{xy}](/images/math/7/2/5/72500c17d10d6bf99f9c071ac752f9d6.png)
The fiber bundle yields a foliation by fibers 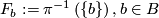 . Its space of leaves
. Its space of leaves  is (diffeomeorphic) homeomorphic to
is (diffeomeorphic) homeomorphic to  , in particular
, in particular  is a Hausdorff manifold.
is a Hausdorff manifold.
2.2 Suspensions
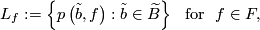
where 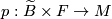 is the canonical projection. This foliation is called the suspension of the representation
is the canonical projection. This foliation is called the suspension of the representation 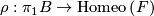 .
.
In particular, if 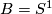 and
and 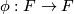 is a homeomorphism of
is a homeomorphism of  , then the suspension foliation of
, then the suspension foliation of  is defined to be the suspension foliation of the representation
is defined to be the suspension foliation of the representation  given by
given by 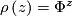 . Its space of leaves is
. Its space of leaves is 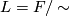 , where
, where 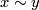 if
if 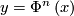 for some
for some 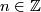 .
.
The simplest examples of suspensions are the Kronecker foliations 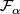 of the 2-torus, that is the suspension foliation of the rotation
of the 2-torus, that is the suspension foliation of the rotation 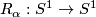 by angle
by angle 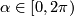 .
If
.
If  is a rational multiple of
is a rational multiple of 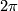 , then the leaves of
, then the leaves of 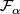 are compact. If
are compact. If  is an irrational multiple of
is an irrational multiple of 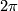 , then the leaves of
, then the leaves of 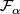 are dense on the 2-torus.
are dense on the 2-torus.
2.3 Submersions
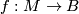
 is foliated by the preimages
is foliated by the preimages 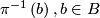 . This includes the case of fiber bundles.
. This includes the case of fiber bundles.
An example of a submersion, which is not a fiber bundle, is given by
![\displaystyle f:\left[-1,1\right]\times {\mathbb R}\rightarrow{\mathbb R}](/images/math/0/5/2/052fdc10e3d29facd86cb6b6e41e53de.png)
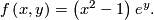
![\left[-1,1\right]\times{\mathbb R}](/images/math/5/e/0/5e00477f106f9f9bfc1dcd3bfb0c4693.png) which is invariant under the
which is invariant under the 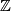 -actions given by
-actions given by 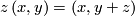
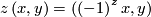
for ![\left(x,y\right)\in\left[-1,1\right]\times{\mathbb R}, z\in{\mathbb Z}](/images/math/e/c/1/ec1378db59bcd94449abc3a736c7e8d2.png) . The induced foliations of
. The induced foliations of ![{\mathbb Z}\backslash \left(\left[-1,1\right]\times{\mathbb R}\right)](/images/math/0/1/e/01ee19ac50fc1824419d5eb447938895.png) are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliaton (of the Möbius band). Their leaf spaces are not Hausdorff.
are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliaton (of the Möbius band). Their leaf spaces are not Hausdorff.
2.4 Reeb foliations
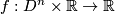
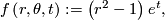
![\left(r,\theta\right)\in \left[0,1\right]\times S^{n-1}](/images/math/3/c/b/3cb41268dbbd7e42abfb3366f15c615a.png) are cylindrical coordinates on
are cylindrical coordinates on 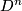 . This submersion yields a foliation of
. This submersion yields a foliation of 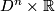 which is invariant under the
which is invariant under the 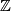 -actions given by
-actions given by 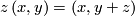
for 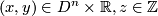 . The induced foliation of
. The induced foliation of 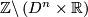 is called the n-dimensional Reeb foliation. Its leaf space is not Hausdorff.
is called the n-dimensional Reeb foliation. Its leaf space is not Hausdorff.
2.5 Taut foliations
A codimension one foliation  of
of  is taut if for every leaf
is taut if for every leaf  of
of  there is a circle transverse to
there is a circle transverse to  which intersects
which intersects  .
.
3 References
- [Godbillon1991] C. Godbillon, Feuilletages, Birkhäuser Verlag, 1991. MR1120547 (93i:57038) Zbl 0724.58002
4 External links
- The Encylopedia of Mathematics article on foliations
- The Wikipedia page about foliations

