Foliation
From Manifold Atlas
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Introduction
1 Foliations
Let be an
be an  -manifold, possibly with boundary, and let
-manifold, possibly with boundary, and let 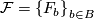 be a decomposition of
be a decomposition of  into connected, topologically immersed submanifolds of dimension
into connected, topologically immersed submanifolds of dimension  .
. 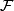 is said to be a codimension
is said to be a codimension  (smooth) foliation of
(smooth) foliation of  if
if  admits an (smooth) atlas
admits an (smooth) atlas 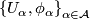 of foliated charts, that is (diffeomorphisms) homeomorphisms
of foliated charts, that is (diffeomorphisms) homeomorphisms 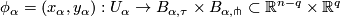
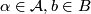 the intersection
the intersection 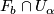 is a union of plaques
is a union of plaques 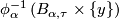 .
.
2 Defining differential form
If  is a smooth, transversely orientable codimension
is a smooth, transversely orientable codimension  foliation and
foliation and  its tangential plane field, then there is a nonsingular
its tangential plane field, then there is a nonsingular  -form
-form 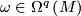 such that, for each
such that, for each 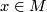 ,
,
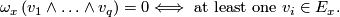
This implies that 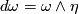 for some
for some 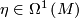 .
.
3 Leaves
The leaves of  are the immersed submanifolds
are the immersed submanifolds 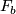 . Each
. Each 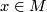 belongs to a unique leaf. The foliation
belongs to a unique leaf. The foliation  determines its tangential plane field
determines its tangential plane field 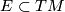 by
by 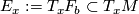 if
if 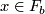 .
.
The space of leaves is 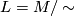 with the quotient topology, where
with the quotient topology, where 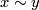 if and only if
if and only if  and
and  belong to the same leaf of
belong to the same leaf of  .
.
4 Holonomy Cocycle
The holonomy cocycle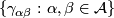 of the atlas is given by
of the atlas is given by 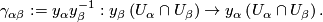
A smooth foliation 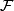 is said to be transversely orientable if
is said to be transversely orientable if 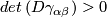 everywhere.
everywhere.
</wikitex>
2 Definition
...
3 Examples
...