Fake projective spaces in dim 6 (Ex)
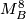 be a closed Milnor manifold. There exist a natural degree 1 normal map
be a closed Milnor manifold. There exist a natural degree 1 normal map 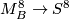 which induces a degree 1 normal map
which induces a degree 1 normal map 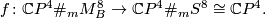
We may pull back the Hopf bundle 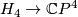 to
to 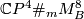 . The sphere bundle of the Hopf bundle over sphere is the true sphere, hence we get a map:
. The sphere bundle of the Hopf bundle over sphere is the true sphere, hence we get a map:
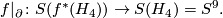
Prove the following:
Lemma 0.1. The map induced above is a degree 1 normal map.
Now, since we are working between odd dimensional manifolds we can by surgery below middle dimension assume that 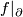 bordant to a homotopy equivalence
bordant to a homotopy equivalence  . Thus by Poincare Conjecture it is indeed normally bordant to a PL-homeomorphism. Choose
. Thus by Poincare Conjecture it is indeed normally bordant to a PL-homeomorphism. Choose ![W'\to S^9\times[0,1]](/images/math/2/8/c/28c9e5199771985065257f4fbbe09c1c.png) to be such bordism.
to be such bordism.
![\displaystyle \bar{g}\colon W'\cup_\partial D(f^*(H_4))\to D(H_4)\cup_\partial S^9\times [0,1]\cong D(H_4)](/images/math/7/c/a/7ca01b2d8568f20d13553583113a7158.png)
Describe these surgeries.
We obtain a manifold with boundary 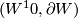 homotopy homotopy equivalent to
homotopy homotopy equivalent to 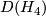 with boundary PL-homeomorphic to
with boundary PL-homeomorphic to 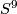 . Thus we may cone off common boundaries extending the homotopy equivalence at the same time. We define
. Thus we may cone off common boundaries extending the homotopy equivalence at the same time. We define
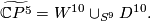
Lemma 0.3.
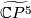 and
and 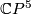 are not homeomorphic.
are not homeomorphic.
Prove the above lemma.
The above construction gives us a degree 1 normal map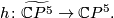
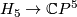 over
over 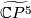 . By the Poincaré conjecture, the sphere bundle
. By the Poincaré conjecture, the sphere bundle 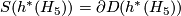 is
is  -homeomorphic to the sphere
-homeomorphic to the sphere 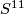 .
. 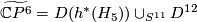 is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
Similarly we may form the connected sum 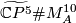 , where
, where 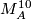 is the Kervaire manifold, and once again, we take pullback of
is the Kervaire manifold, and once again, we take pullback of 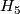 line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence
line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence 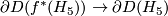 we have to use a little bit of surgery.
we have to use a little bit of surgery.
Describe these surgeries.
Nevertheless there exists a manifold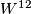 such that
such that 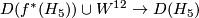
 -homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
-homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
Lemma 0.4.
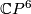 ,
, 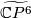 and
and 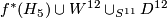 , are topologically distinct homotopy projective spaces.
, are topologically distinct homotopy projective spaces.
The aim of this exercise is to write full details of proof of the above Lemma (which is Lemma 8.24 form [Madsen&Milgram1979]).
A sketch of this proof can be found in the book, on page 170.
References
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002