Fake projective spaces in dim 6 (Ex)
From Manifold Atlas
Revision as of 14:59, 23 March 2012 by Marek Kaluba (Talk | contribs)
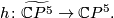
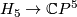 over
over 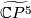 . By the Poincaré conjecture, the sphere bundle
. By the Poincaré conjecture, the sphere bundle 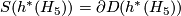 is
is  -homeomorphic to the sphere
-homeomorphic to the sphere 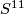 .
. 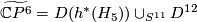 is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
Similarly we may form the connected sum
is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
Similarly we may form the connected sum 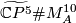 , where
, where 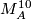 is the Kervaire manifold, and once again, we take pullback of
is the Kervaire manifold, and once again, we take pullback of 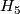 line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence
line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence 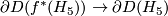 we have to use a little bit of surgery. Nevertheless there exists a manifold
we have to use a little bit of surgery. Nevertheless there exists a manifold 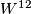 such that
such that 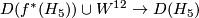
 -homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
-homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
Lemma 0.1.
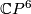 ,
, 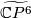 and
and 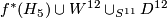 , are topologically distinct homotopy projective spaces.
, are topologically distinct homotopy projective spaces.
The aim of this exercise is to write full details of proof of Lemma 8.24 form [Madsen&Milgram1979].
A sketch of this proof can be found in the book, on page 170.
References
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002