Fake projective spaces in dim 6 (Ex)

From Manifold Atlas
(Difference between revisions)
Jump to: navigation, search
m
m
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
<wikitex>;
<wikitex>;
+
Let $M_B^8$ be a closed [[Milnor manifold]]. There exist a natural degree 1 normal map $M_B^8\to S^8$ which induces a degree 1 normal map $$f\colon\mathbb{C}P^4\#_mM_B^8\to \mathbb{C}P^4\#_m S^8\cong \mathbb{C}P^4.$$
−
There is a degree 1 normal map $$h\colon\widetilde{\mathbb{C}P^5}\to \mathbb{C}P^5.$$ We may pull back the canonical line bundle $H_5\to \mathbb{C}P^5$ over $\widetilde{\mathbb{C}P^5}$. By the Poincaré conjecture, the sphere bundle $S(h^*(H_5))=\partial D(h^*(H_5))$ is $PL$-homeomorphic to the sphere $S^{11}$. $\widetilde{\mathbb{C}P^6}=D(h^*(H_5))\cup_{S^{11}}D^{12}$ is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
+
We may pull back the Hopf bundle $H_4\to \mathbb{C}P^4$ to $\mathbb{C}P^4\#_mM_B^8$. The sphere bundle of the Hopf bundle over sphere is the true sphere, hence we get a map:
+
$$f|_\partial\colon S(f^*(H_4))\to S(H_4)=S^9.$$
+
'''Prove the following:'''
+
\begin{lemma}
+
The map induced above is a degree 1 normal map.
+
\end{lemma}
−
Similarly we may form the connected sum $\widetilde{\mathbb{C}P^5}\# M^{10}_A$, where $M^{10}_A$ is the [[Kervaire_sphere|Kervaire manifold]], and once again, we take pullback of $H_5$ line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence $\partial D(f^*(H_5))\to \partial D(H_5)$ we have to use a little bit of surgery. Nevertheless there exists a manifold $W^{12}$ such that $$D(f^*(H_5))\cup W^{12}\to D(H_5)$$ is a homotopy equivalence of manifolds with boundary. Again since the boundary is already $PL$-homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
+
Now, since we are working between odd dimensional manifolds we can by surgery below middle dimension assume that $f|_\partial$ bordant to a homotopy equivalence $g$. Thus by Poincare Conjecture it is indeed normally bordant to a PL-homeomorphism. Choose $W'\to S^9\times[0,1]$ to be such bordism.
+
+
\begin{lemma} We can perform surgery on $$\bar{g}\colon W'\cup_\partial D(f^*(H_4))\to D(H_4)\cup_\partial S^9\times [0,1]\cong D(H_4)$$ to make it a homotopy equivalence.
+
\end{lemma}
+
+
'''Describe these surgeries.'''
+
+
We obtain a manifold with boundary $(W^10,\partial W)$ homotopy homotopy equivalent to $D(H_4)$ with boundary PL-homeomorphic to $S^9$. Thus we may cone off common boundaries extending the homotopy equivalence at the same time. We define
+
$$\widetilde{\mathbb{C}P^5}=W^{10}\cup_{S^9}D^{10}.$$
+
+
\begin{lemma}
+
$\widetilde{\mathbb{C}P^5}$ and $\mathbb{C}P^5$ are not homeomorphic.
+
\end{lemma}
+
+
'''Prove the above lemma.'''
+
+
However, the construction above gives us a degree 1 normal map $$h\colon\widetilde{\mathbb{C}P^5}\to \mathbb{C}P^5.$$ We may pull back the canonical line bundle $H_5\to \mathbb{C}P^5$ over $\widetilde{\mathbb{C}P^5}$. By the Poincaré conjecture, the sphere bundle $S(h^*(H_5))=\partial D(h^*(H_5))$ is $PL$-homeomorphic to the sphere $S^{11}$. $\widetilde{\mathbb{C}P^6}=D(h^*(H_5))\cup_{S^{11}}D^{12}$ is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.
+
+
Similarly we may form the connected sum $\widetilde{\mathbb{C}P^5}\# M^{10}_A$, where $M^{10}_A$ is the [[Kervaire_sphere|Kervaire manifold]], and once again, we take pullback of $H_5$ line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence $\partial D(f^*(H_5))\to \partial D(H_5)$ we have to use a little bit of surgery.
+
+
'''Describe these surgeries.'''
+
+
Nevertheless there exists a manifold $W^{12}$ such that $$D(f^*(H_5))\cup W^{12}\to D(H_5)$$ is a homotopy equivalence of manifolds with boundary. Again since the boundary is already $PL$-homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.
{{beginthm|Lemma}}
{{beginthm|Lemma}}
Line 9: Line 37:
{{endthm}}
{{endthm}}
−
The aim of this exercise is to write full details of proof of Lemma 8.24 form \cite{Madsen&Milgram1979}.
+
The aim of this exercise is to '''write full details of proof of the above Lemma''' (which is Lemma 8.24 form \cite{Madsen&Milgram1979}).
A sketch of this proof can be found in the book, on page 170.
A sketch of this proof can be found in the book, on page 170.
Line 16: Line 44:
{{#RefList:}}
{{#RefList:}}
[[Category:Exercises]]
[[Category:Exercises]]
+
[[Category:Exercises without solution]]

Latest revision as of 00:15, 3 April 2012

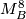Let M_B^8 be a closed Milnor manifold. There exist a natural degree 1 normal map 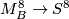M_B^8\to S^8 which induces a degree 1 normal map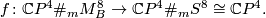
\displaystyle f\colon\mathbb{C}P^4\#_mM_B^8\to \mathbb{C}P^4\#_m S^8\cong \mathbb{C}P^4.

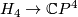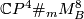We may pull back the Hopf bundle H_4\to \mathbb{C}P^4 to \mathbb{C}P^4\#_mM_B^8. The sphere bundle of the Hopf bundle over sphere is the true sphere, hence we get a map:

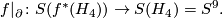
\displaystyle f|_\partial\colon S(f^*(H_4))\to S(H_4)=S^9.

Prove the following:

Lemma 0.1. The map induced above is a degree 1 normal map.

Now, since we are working between odd dimensional manifolds we can by surgery below middle dimension assume that 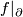f|_\partial bordant to a homotopy equivalence g. Thus by Poincare Conjecture it is indeed normally bordant to a PL-homeomorphism. Choose W'\to S^9\times[0,1] to be such bordism.

Lemma 0.2. We can perform surgery on
\displaystyle \bar{g}\colon W'\cup_\partial D(f^*(H_4))\to D(H_4)\cup_\partial S^9\times [0,1]\cong D(H_4)
to make it a homotopy equivalence.

Describe these surgeries.

We obtain a manifold with boundary 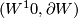(W^10,\partial W) homotopy homotopy equivalent to 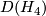D(H_4) with boundary PL-homeomorphic to 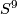S^9. Thus we may cone off common boundaries extending the homotopy equivalence at the same time. We define

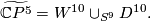
\displaystyle \widetilde{\mathbb{C}P^5}=W^{10}\cup_{S^9}D^{10}.

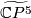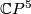Lemma 0.3. \widetilde{\mathbb{C}P^5} and \mathbb{C}P^5 are not homeomorphic.

Prove the above lemma.

However, the construction above gives us a degree 1 normal map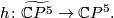
\displaystyle h\colon\widetilde{\mathbb{C}P^5}\to \mathbb{C}P^5.
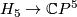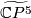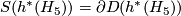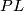We may pull back the canonical line bundle H_5\to \mathbb{C}P^5 over \widetilde{\mathbb{C}P^5}. By the Poincaré conjecture, the sphere bundle S(h^*(H_5))=\partial D(h^*(H_5)) is PL-homeomorphic to the sphere 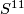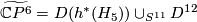S^{11}. \widetilde{\mathbb{C}P^6}=D(h^*(H_5))\cup_{S^{11}}D^{12} is a homotopy complex projective space obtained by coning off the boundary of the disk bundle.

Similarly we may form the connected sum 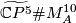\widetilde{\mathbb{C}P^5}\# M^{10}_A, where 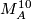M^{10}_A is the Kervaire manifold, and once again, we take pullback of 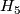H_5 line bundle via the natural degree 1 normal map. Now to obtain a homotopy equivalence 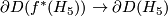\partial D(f^*(H_5))\to \partial D(H_5) we have to use a little bit of surgery.

Describe these surgeries.

Nevertheless there exists a manifold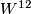 W^{12} such that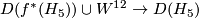
\displaystyle D(f^*(H_5))\cup W^{12}\to D(H_5)
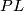is a homotopy equivalence of manifolds with boundary. Again since the boundary is already PL-homeomorphic to a sphere we may extend the homotopy equivalence after coning off the boundaries.

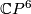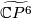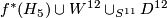Lemma 0.4. \mathbb{C}P^6, \widetilde{\mathbb{C}P^6} and f^*(H_5)\cup W^{12}\cup_{S^{11}}D^{12}, are topologically distinct homotopy projective spaces.

The aim of this exercise is to write full details of proof of the above Lemma (which is Lemma 8.24 form [Madsen&Milgram1979]).

A sketch of this proof can be found in the book, on page 170.

References

Retrieved from "http://www.map.mpim-bonn.mpg.de/index.php?title=Fake_projective_spaces_in_dim_6_(Ex)&oldid=8771"
Personal tools
Namespaces
Variants
Actions
Navigation
Interaction
Toolbox