Fake complex projective spaces
Contents |
1 Introduction
A fake complex projective space is a topological manifold which is homotopy equivalent to a complex projective space 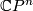 for some
for some  .
.
2 Construction and examples
Given a free tame action of the circle on a 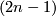 -sphere, the orbit space is a fake
-sphere, the orbit space is a fake 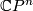 . On the other hand, if
. On the other hand, if  is a closed manifold, any homotopy equivalence
is a closed manifold, any homotopy equivalence 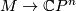 induces a principal
induces a principal  -bundle over
-bundle over  whose total space is homeomorphic to
whose total space is homeomorphic to 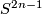 . We obtain the following result:
. We obtain the following result:
Proposition 2.1.
The surgery structure set of 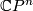 is in bijection to the set of free tame circle actions on
is in bijection to the set of free tame circle actions on 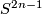 modulo
modulo  -equivariant homeomorphism.
-equivariant homeomorphism.
3 Invariants
Obviously the homology and homotopy groups of a fake complex projective space are isomorphic to the ones of the 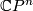 . Different fake complex projective spaces may be distinguished using the so-called splitting invariants. More precisely, for any
. Different fake complex projective spaces may be distinguished using the so-called splitting invariants. More precisely, for any 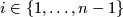 , there is a function
, there is a function
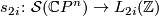
from the surgery structure set of 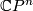 to the
to the  -groups of the integers, where
-groups of the integers, where 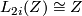 if
if  is even, and
is even, and 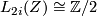 if
if  is odd.
is odd.
Theorem 3.1. The cartesian product
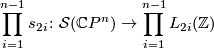
is a bijection.
Thus, all possible combination of splitting invariants are realized by elements in the structure set, and two elements of the structure set agree if and only if all the splitting invariants agree.
The splitting invariant 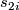 is defined as follows: Given an element
is defined as follows: Given an element 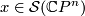 , represent it by homotopy equivalence
, represent it by homotopy equivalence 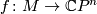 which is transverse to
which is transverse to 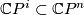 . The restriction of
. The restriction of  to a map
to a map 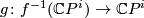 may fail to be a homotopy equivalence, but it is still a degree one normal map. Hence the surgery obstruction
may fail to be a homotopy equivalence, but it is still a degree one normal map. Hence the surgery obstruction 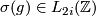 of
of  is defined. Let
is defined. Let 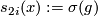 .
.
4 Classification/Characterization
...
5 Further discussion
...