Dynamics of foliations
(→Growth in groups) |
m (→Growth in groups) |
||
| (19 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
<wikitex>; | <wikitex>; | ||
Foliations of Riemannian manifolds can be considered as multidimensional dynamical systems: Riemannian structure (more precisely, Riemannian structure along the leaves) plays the role of time, the leaves play the role of orbits \cite{Walczak2004}. The dynamics of a foliation can be described in terms of its holonomy (see [[Foliations#Holonomy]]) pseudogroup. As far as we know, the notion of a pseudogroup appeared for the | Foliations of Riemannian manifolds can be considered as multidimensional dynamical systems: Riemannian structure (more precisely, Riemannian structure along the leaves) plays the role of time, the leaves play the role of orbits \cite{Walczak2004}. The dynamics of a foliation can be described in terms of its holonomy (see [[Foliations#Holonomy]]) pseudogroup. As far as we know, the notion of a pseudogroup appeared for the | ||
| − | first time in \cite{Veblen&Whitehead1932} in the context of geometric objects studied in differential geometry. Pseudogroups have been brought into the foliation theory by Haefliger \cite{Haefliger1962a}. The growth types of leaves (equivalent to the growth types of the corresponding orbits of holonomy pseudogroups) as well as the expansion growth of a foliation (or, its holonomy pseudogroup) describe some aspects of the foliation dynamics. Corresponding to the expansion growth is the notion of geometric entropy of a foliation \cite{Ghys&Langevin&Walczak1988}. Vanishing entropy can be seen as a dynamical condition which occurs to have strong geometric and topological consequences (see [[Dynamics of foliations#Results on entropy]]) below. | + | first time in \cite{Veblen&Whitehead1932} in the context of geometric objects studied in differential geometry. Pseudogroups have been brought into the foliation theory by Haefliger \cite{Haefliger1962a}. The growth types of leaves (equivalent to the growth types of the corresponding orbits of holonomy pseudogroups) as well as the expansion growth of a foliation (or, its holonomy pseudogroup) describe some aspects of the foliation dynamics. Corresponding to the expansion growth is the notion of geometric entropy of a foliation \cite{Ghys&Langevin&Walczak1988}. Vanishing entropy can be seen as a dynamical condition which occurs to have strong geometric and topological consequences (see [[Dynamics of foliations#Results on entropy]]) below.</wikitex> |
| − | </wikitex> | + | |
| − | + | ||
| − | + | ||
== Pseudogroups == | == Pseudogroups == | ||
| Line 57: | Line 54: | ||
\label{def:psgroup}{{endthm}} | \label{def:psgroup}{{endthm}} | ||
| − | |||
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, $C^k$, $k = 1, 2, \ldots, \infty, \omega$, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group $G$ of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is '''generated''' by $G$.) | As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, $C^k$, $k = 1, 2, \ldots, \infty, \omega$, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group $G$ of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is '''generated''' by $G$.) | ||
Any set $A$ of homeomorphisms bewteen open sets (with domains covering a space $X$) generates ma pseudogroup $\Gamma (A)$ which is the smallest pseudogroup containing $A$; precisely a homeomorphism $h:D_h\to R_h$ belongs to $\Gamma (A)$ if and only if for any point $x\in D_h$ there exist elements $h_1, \ldots, h_k\in A$, exponents $\epsilon _1, \ldots, \epsilon _k\in\{ \pm 1\}$ and a neighbourhood $V$ of $x$ such that $h = h_1^{\epsilon _1}\circ\ldots\circ h_k^{\epsilon _k}$ on $V$. If $A$ is finite, $\Gamma (A)$ is said to be '''finitely generated'''. | Any set $A$ of homeomorphisms bewteen open sets (with domains covering a space $X$) generates ma pseudogroup $\Gamma (A)$ which is the smallest pseudogroup containing $A$; precisely a homeomorphism $h:D_h\to R_h$ belongs to $\Gamma (A)$ if and only if for any point $x\in D_h$ there exist elements $h_1, \ldots, h_k\in A$, exponents $\epsilon _1, \ldots, \epsilon _k\in\{ \pm 1\}$ and a neighbourhood $V$ of $x$ such that $h = h_1^{\epsilon _1}\circ\ldots\circ h_k^{\epsilon _k}$ on $V$. If $A$ is finite, $\Gamma (A)$ is said to be '''finitely generated'''. | ||
| − | |||
</wikitex> | </wikitex> | ||
| Line 194: | Line 189: | ||
For most of results listed here we refer to \cite{Hector&Hirsch1981}. | For most of results listed here we refer to \cite{Hector&Hirsch1981}. | ||
| − | Let $G$ be a finitely generated group and $G_1$ a finite | + | Let $G$ be a finitely generated group and $G_1$ a finite \it{symmetric} |
(i.e. such that $e\in G_1$ and $G_1^{-1} = \{ g^{-1};\, g\in G_1\}\subset G_1$) | (i.e. such that $e\in G_1$ and $G_1^{-1} = \{ g^{-1};\, g\in G_1\}\subset G_1$) | ||
set generating it. For any $n\in\Bbb N$ let | set generating it. For any $n\in\Bbb N$ let | ||
| Line 204: | Line 199: | ||
The type of growth of $t_G$ does not depend on $G_1$, so we may write the following. | The type of growth of $t_G$ does not depend on $G_1$, so we may write the following. | ||
| − | {{beginthm|Definition}} The '''growth type''' | + | {{beginthm|Definition}} The '''growth type''' |
$gr (G)$ of $G$ is defined as $[t_G]$ for any finite symmetric generating set $G_1$. If $G$ | $gr (G)$ of $G$ is defined as $[t_G]$ for any finite symmetric generating set $G_1$. If $G$ | ||
acts on a space $X$ and $x\in X$, then the '''growth type''' $gr (G,x)$ of $G$ at $x$ | acts on a space $X$ and $x\in X$, then the '''growth type''' $gr (G,x)$ of $G$ at $x$ | ||
| Line 212: | Line 207: | ||
{{endthm}} | {{endthm}} | ||
| − | {{beginthm|Example}} A finite group has the growth type $[1]$ while the | + | {{beginthm|Example}} A finite group has the growth type $[1]$ while the |
abelian group $\Bbb Z^d$ has the polynomial growth of degree $d$. Any free | abelian group $\Bbb Z^d$ has the polynomial growth of degree $d$. Any free | ||
(non-abelian) group has the exponential growth $[e^n]$. | (non-abelian) group has the exponential growth $[e^n]$. | ||
{{endthm}} | {{endthm}} | ||
| − | {{beginthm|Proposition}}For any finitely generated group $G$ and | + | {{beginthm|Proposition}} For any finitely generated group $G$ and |
| − | any normal subgroup $H$ of $G$ we have | + | any normal subgroup $H$ of $G$ we have $gr (G/H)\preceq gr (G)\preceq [e^n].$ |
| − | $ | + | |
{{endthm}} | {{endthm}} | ||
| + | |||
| + | {{beginthm|Proposition}} Any finitely generated abelian group of rank $d$ has the growth type $[n^d]$. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Theorem}} Any finitely generated nilpotent group is of polynomial type of growth. Moreover, if a finitely generated group contains a nilpotent group of finite index, then it has a polynomial type of growth \cite{Wolf1968}. Conversely, any finitely generated group of polynomial type of growth contains a nilpotent subgroup of finite index \cite{Gromov1981}. | ||
| + | {{endthm}} | ||
| + | |||
| + | Natural examples of finitely generated groups are provided by | ||
| + | fundamental groups of compact manifolds. Below we show how the growth type | ||
| + | of the fundamental group of a compact Riemannian manifold is related to | ||
| + | its geometry. To this end let us consider a | ||
| + | complete Riemannian manifold $M$, fix a point $x\in M$ and let | ||
| + | $$t_M(n) = vol B(x,n),$$ | ||
| + | where $B(x,r)$ is the ball on $M$ of radius $r$ and centre $x$ while $vol$ | ||
| + | is the measure on $M$ induced by the Riemannian structure. If $x'$ is another point of $M$, then $B(x',r)\subset B(x, r + r_0)$, where $r_0 = | ||
| + | d(x, x')$ and $d$ is the distance function on $M$. | ||
| + | Therefore, the following definition is correct. | ||
| + | |||
| + | {{beginthm|Definition}} $gr (M) = [t_M]$ is called the '''growth type''' of a Riemannian manifold $M$. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Proposition|(\cite{Milnor1968a}, \cite{Švarc1955})}} If $M$ is compact, then the fundamental group $\pi_1 (M)$ and the universal covering $\tilde M$ of $M$ have the same growth type. If $M$ is a compact Riemannian manifold of negative sectional | ||
| + | curvature, then both $\tilde M$ and $\pi_1(M)$ have exponential growth. | ||
| + | {{endthm}} | ||
| + | |||
| + | Fundamental groups of compact manifolds of negative sectional curvature are hyperbolic in the sense of \cite{Gromov1987}. The last statement of the Proposition above can be generalized as follows, | ||
| + | |||
| + | {{beginthm|Proposition}} Any non-elementary hyperbolic group has exponential growth. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Latest revision as of 17:40, 10 December 2010
|
The user responsible for this page is Pawel Walczak. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Foliations of Riemannian manifolds can be considered as multidimensional dynamical systems: Riemannian structure (more precisely, Riemannian structure along the leaves) plays the role of time, the leaves play the role of orbits [Walczak2004]. The dynamics of a foliation can be described in terms of its holonomy (see Foliations#Holonomy) pseudogroup. As far as we know, the notion of a pseudogroup appeared for the first time in [Veblen&Whitehead1932] in the context of geometric objects studied in differential geometry. Pseudogroups have been brought into the foliation theory by Haefliger [Haefliger1962a]. The growth types of leaves (equivalent to the growth types of the corresponding orbits of holonomy pseudogroups) as well as the expansion growth of a foliation (or, its holonomy pseudogroup) describe some aspects of the foliation dynamics. Corresponding to the expansion growth is the notion of geometric entropy of a foliation [Ghys&Langevin&Walczak1988]. Vanishing entropy can be seen as a dynamical condition which occurs to have strong geometric and topological consequences (see Dynamics of foliations#Results on entropy) below.
2 Pseudogroups
The notion of a pseudogroup generalizes that of a group of
transformations. Given a space  , any group of transformations of
, any group of transformations of  consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo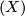 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 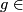 Homeo
Homeo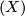 , then
, then
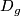 is its domain and
is its domain and 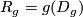 .
.
Definition 2.1.
A subfamily  of Homeo
of Homeo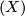 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,  should satisfy the following conditions:
should satisfy the following conditions:
(i) 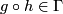 whenever
whenever  and
and 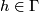 ,
,
(ii) 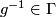 whenever
whenever 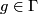 ,
,
(iii) 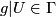 whenever
whenever 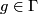 and
and 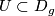 is
open,
is
open,
(iv) if 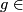 Homeo
Homeo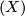 ,
, 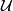 is an open cover of
is an open cover of 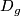 and
and
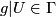 for any
for any 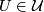 , then
, then 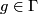 .
.
Moreover, we shall always assume that
(v] id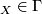 (or, equivalently,
(or, equivalently, 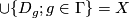 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 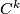 ,
, 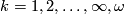 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 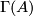 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 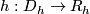 belongs to
belongs to 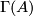 if and only if for any point
if and only if for any point 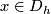 there exist elements
there exist elements 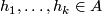 , exponents
, exponents 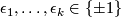 and a neighbourhood
and a neighbourhood  of
of  such that
such that 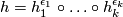 on
on  . If
. If  is finite,
is finite, 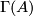 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 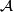 on a foliated manifold
on a foliated manifold 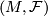 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 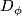 of the charts
of the charts 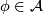 ) if
) if
(i) the covering 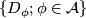 is locally finite,
is locally finite,
(ii) for any 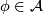 ,
, 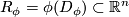 is an open cube,
is an open cube,
(iii) if 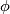 and
and 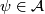 , and
, and 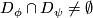 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 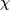 and such that
and such that
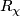 is an open cube,
is an open cube, 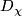 contains the closure of
contains the closure of 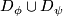 and
and 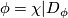 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 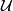 of a foliated manifold
of a foliated manifold 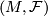 . For
any
. For
any 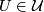 , let
, let 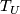 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 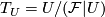 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 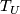 is homeomorphic
(
is homeomorphic
(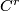 -diffeomorphic when
-diffeomorphic when  is
is 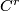 -differentiable and
-differentiable and 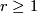 ) to an
open cube
) to an
open cube 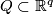 (
(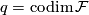 ) via the map
) via the map
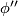 , where
, where 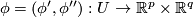 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
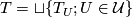
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class 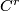 ,
,  , each of the spaces
, each of the spaces 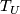 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a 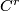 -submanifold
-submanifold 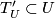 transverse to
transverse to  : if
: if 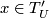 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
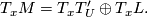
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 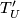 .
.
Definition 3.2. Given a nice covering 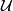 of a foliated manifold
of a foliated manifold 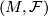 and two sets
and two sets  and
and 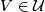 such that
such that 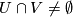 the holonomy map
the holonomy map 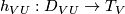 ,
,
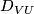 being the open subset of
being the open subset of 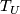 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 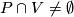 , is defined in the following
way:
, is defined in the following
way:
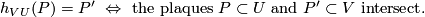
All the maps 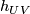 (
(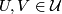 ) generate a pseudogroup
) generate a pseudogroup 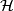 on
on  .
.
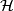 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 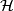 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 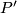 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
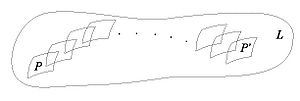
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 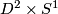 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 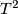 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 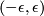 (
( ), the point of intersection
), the point of intersection 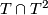 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 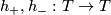 such that
such that 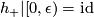 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 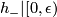 contract their domains towards
contract their domains towards  .
.
4 Growth
Let us begin with two non-decreasing sequences 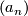 and
and 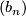 of
non-negative numbers. We shall say that
of
non-negative numbers. We shall say that 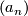 "grows slower" that
"grows slower" that
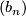 (
(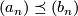 ) whenever there exist positive constants
) whenever there exist positive constants  and
and  such that the inequalities
such that the inequalities
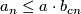
hold for all 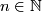 . We say that types of growth
of our sequences
. We say that types of growth
of our sequences 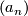 and
and 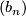 are the same whenever
are the same whenever
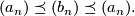
Let now 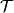 be the set of non-negative increasing functions defined on
be the set of non-negative increasing functions defined on
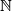 :
:
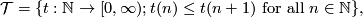
and 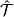 the set of increasing sequences with entries in
the set of increasing sequences with entries in 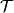 :
:
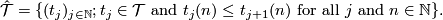
Elements  of
of 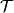 can be identified with sequences
can be identified with sequences 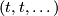 , so
, so
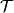 can be considered as a subset of
can be considered as a subset of 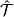 .
.
A preorder  defined by the condition:
defined by the condition:
(*) 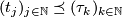 if and only
if there exists
if and only
if there exists 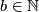 such that for all
such that for all 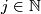 the inequalities
the inequalities
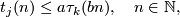
induces an equivalence relation 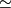 in
in 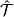 :
:
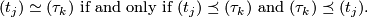
In particular, if  and
and 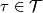 , then
, then
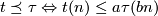
and
![\displaystyle t\simeq\tau\Leftrightarrow a^{-1}\tau ([n/b] )\le t(n)\le a\tau (bn)](/images/math/3/9/9/39920075762460750ebcb56e656ecd68.png)
for all 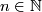 and some
and some 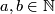 . (Here,
. (Here, ![[x]](/images/math/f/8/d/f8d486cee86578cfe4fddaf090863ff4.png) is the largest
integer which does not exceed
is the largest
integer which does not exceed  ,
, 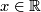 .)
.)
Definition 4.1. Elements of the quotient 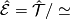 are called
growth types. The growth type of
are called
growth types. The growth type of 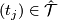 (resp., of
(resp., of 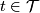 ) is denoted by
) is denoted by ![[(t_j)]](/images/math/9/3/2/9322d2bc60ea96c7550739c46a968a79.png) (resp., by
(resp., by ![[t]](/images/math/a/f/e/afe39aa48eb1ca7f242755040e1b2fec.png) ). Also,
we let
). Also,
we let ![\mathcal{E} = \{ [t];\, t\in\mathcal{T}\}](/images/math/5/f/8/5f8fa4f7ec18b28a4fae049c59f1a1b0.png) .
. 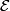 is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
 induces a partial order (denoted again by
induces a partial order (denoted again by  ) in
) in
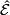 .
.
Example 4.2. ![[0]\preceq [1]\preceq [\log n]\preceq [n]\preceq [n^2]\preceq\dots\preceq [(1, n, n^2, \dots )]\preceq [2^n]\preceq [(1, 2^n, 3^n,\dots )]](/images/math/0/4/6/0466454f7d5dc21e535bfea48de683d1.png) and all the growth types listed above are different. The growth
type of any polynomial of degree
and all the growth types listed above are different. The growth
type of any polynomial of degree 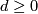 is equal to
is equal to ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) and is called
polynomial (of degree
and is called
polynomial (of degree  ).
). ![[a^n] = [e^n]](/images/math/6/a/a/6aa95a87bcd7ec3c9ae9a43d67a43db7.png) for any
for any  and this growth type is called exponential.
and this growth type is called exponential.
4.1 Growth in groups
For most of results listed here we refer to [Hector&Hirsch1981].
Let  be a finitely generated group and
be a finitely generated group and 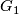 a finite symmetric
(i.e. such that
a finite symmetric
(i.e. such that 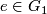 and
and 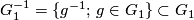 )
set generating it. For any
)
set generating it. For any 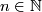 let
let
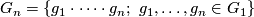
and
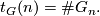
The type of growth of 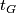 does not depend on
does not depend on 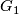 , so we may write the following.
, so we may write the following.
Definition 4.3. The growth type
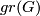 of
of  is defined as
is defined as ![[t_G]](/images/math/e/d/0/ed0a8200ade2d557c1f80768b8aeed7e.png) for any finite symmetric generating set
for any finite symmetric generating set 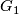 . If
. If  acts on a space
acts on a space  and
and 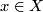 , then the growth type
, then the growth type 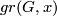 of
of  at
at  is defined in a similar way:
is defined in a similar way: ![gr (G,x) = [t_x]](/images/math/e/b/4/eb46244165e9f374642fba6efe2cbf30.png) , where
, where
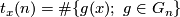
for any fixed finite symmetric generating set 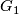 .
.
Example 4.4. A finite group has the growth type ![[1]](/images/math/e/f/1/ef1046ca56d6240cc302cb4a5fdb301c.png) while the
abelian group
while the
abelian group 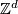 has the polynomial growth of degree
has the polynomial growth of degree  . Any free
(non-abelian) group has the exponential growth
. Any free
(non-abelian) group has the exponential growth ![[e^n]](/images/math/3/a/6/3a6f983ab43d8e3f848fab287b391a56.png) .
.
Proposition 4.5. For any finitely generated group  and
any normal subgroup
and
any normal subgroup  of
of  we have
we have ![gr (G/H)\preceq gr (G)\preceq [e^n].](/images/math/0/2/e/02ee95d5b465acf28e785980f448a21e.png)
Proposition 4.6. Any finitely generated abelian group of rank  has the growth type
has the growth type ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) .
.
Theorem 4.7. Any finitely generated nilpotent group is of polynomial type of growth. Moreover, if a finitely generated group contains a nilpotent group of finite index, then it has a polynomial type of growth [Wolf1968]. Conversely, any finitely generated group of polynomial type of growth contains a nilpotent subgroup of finite index [Gromov1981].
Natural examples of finitely generated groups are provided by
fundamental groups of compact manifolds. Below we show how the growth type
of the fundamental group of a compact Riemannian manifold is related to
its geometry. To this end let us consider a
complete Riemannian manifold  , fix a point
, fix a point 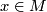 and let
and let
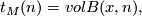
where 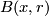 is the ball on
is the ball on  of radius
of radius  and centre
and centre  while
while 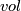 is the measure on
is the measure on  induced by the Riemannian structure. If
induced by the Riemannian structure. If 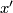 is another point of
is another point of  , then
, then 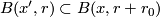 , where
, where 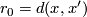 and
and  is the distance function on
is the distance function on  .
Therefore, the following definition is correct.
.
Therefore, the following definition is correct.
Definition 4.8. ![gr (M) = [t_M]](/images/math/0/5/d/05db23e360caae209afbf3bf0b30fc43.png) is called the growth type of a Riemannian manifold
is called the growth type of a Riemannian manifold  .
.
Proposition 4.9 ([Milnor1968a], [Švarc1955]). If  is compact, then the fundamental group
is compact, then the fundamental group 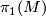 and the universal covering
and the universal covering 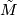 of
of  have the same growth type. If
have the same growth type. If  is a compact Riemannian manifold of negative sectional
curvature, then both
is a compact Riemannian manifold of negative sectional
curvature, then both 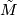 and
and 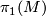 have exponential growth.
have exponential growth.
Fundamental groups of compact manifolds of negative sectional curvature are hyperbolic in the sense of [Gromov1987]. The last statement of the Proposition above can be generalized as follows,
Proposition 4.10. Any non-elementary hyperbolic group has exponential growth.
4.2 Orbit growth in pseudogroups
4.3 Expansion growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Gromov1981] M. Gromov, Groups of polynomial growth and expanding maps, Inst. Hautes Études Sci. Publ. Math. (1981), no.53, 53–73. MR623534 (83b:53041) Zbl 0474.20018
- [Gromov1987] M. Gromov, Hyperbolic groups, Essays in group theory,Math. Sci. Res. Inst. Publ., 8, Springer, New York, (1987) 75–263. MR0919829 (89e:20070) Zbl 0634.20015
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Hector&Hirsch1981] G. Hector and U. Hirsch, Introduction to the geometry of foliations. Part A, Friedr. Vieweg \& Sohn, Braunschweig, 1981. MR639738 (83d:57019) Zbl 0628.57001
- [Milnor1968a] J. Milnor, A note on curvature and fundamental group, J. Differential Geometry 2 (1968), 1–7. MR0232311 (38 #636) Zbl 0162.25401
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022
- [Wolf1968] J. A. Wolf, Growth of finitely generated solvable groups and curvature of Riemanniann manifolds, J. Differential Geometry 2 (1968), 421–446. MR0248688 (40 #1939) Zbl 0207.51803
- [Švarc1955] A. S. Švarc, A volume invariant of coverings, Dokl. Akad. Nauk SSSR (N.S.) 105 (1955), 32–34. MR0075634 (17,781d)
 consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo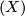 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 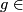 Homeo
Homeo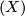 , then
, then
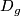 is its domain and
is its domain and 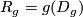 .
.
Definition 2.1.
A subfamily  of Homeo
of Homeo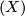 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,  should satisfy the following conditions:
should satisfy the following conditions:
(i) 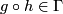 whenever
whenever  and
and 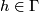 ,
,
(ii) 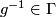 whenever
whenever 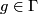 ,
,
(iii) 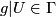 whenever
whenever 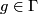 and
and 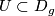 is
open,
is
open,
(iv) if 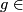 Homeo
Homeo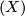 ,
, 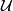 is an open cover of
is an open cover of 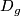 and
and
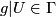 for any
for any 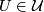 , then
, then 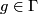 .
.
Moreover, we shall always assume that
(v] id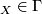 (or, equivalently,
(or, equivalently, 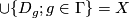 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 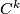 ,
, 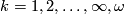 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 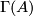 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 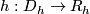 belongs to
belongs to 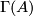 if and only if for any point
if and only if for any point 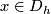 there exist elements
there exist elements 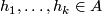 , exponents
, exponents 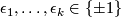 and a neighbourhood
and a neighbourhood  of
of  such that
such that 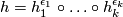 on
on  . If
. If  is finite,
is finite, 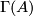 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 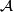 on a foliated manifold
on a foliated manifold 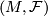 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 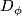 of the charts
of the charts 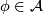 ) if
) if
(i) the covering 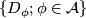 is locally finite,
is locally finite,
(ii) for any 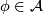 ,
, 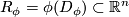 is an open cube,
is an open cube,
(iii) if 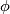 and
and 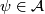 , and
, and 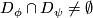 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 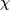 and such that
and such that
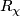 is an open cube,
is an open cube, 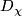 contains the closure of
contains the closure of 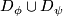 and
and 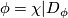 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 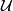 of a foliated manifold
of a foliated manifold 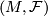 . For
any
. For
any 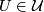 , let
, let 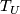 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 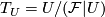 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 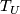 is homeomorphic
(
is homeomorphic
(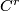 -diffeomorphic when
-diffeomorphic when  is
is 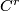 -differentiable and
-differentiable and 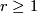 ) to an
open cube
) to an
open cube 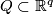 (
(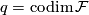 ) via the map
) via the map
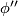 , where
, where 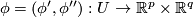 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
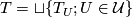
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class 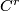 ,
,  , each of the spaces
, each of the spaces 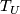 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a 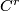 -submanifold
-submanifold 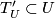 transverse to
transverse to  : if
: if 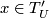 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
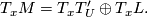
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 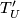 .
.
Definition 3.2. Given a nice covering 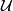 of a foliated manifold
of a foliated manifold 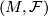 and two sets
and two sets  and
and 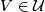 such that
such that 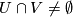 the holonomy map
the holonomy map 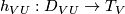 ,
,
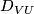 being the open subset of
being the open subset of 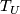 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 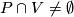 , is defined in the following
way:
, is defined in the following
way:
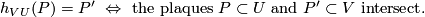
All the maps 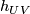 (
(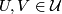 ) generate a pseudogroup
) generate a pseudogroup 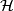 on
on  .
.
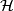 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 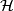 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 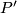 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 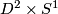 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 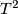 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 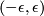 (
( ), the point of intersection
), the point of intersection 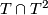 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 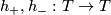 such that
such that 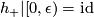 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 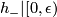 contract their domains towards
contract their domains towards  .
.
4 Growth
Let us begin with two non-decreasing sequences 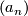 and
and 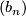 of
non-negative numbers. We shall say that
of
non-negative numbers. We shall say that 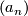 "grows slower" that
"grows slower" that
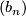 (
(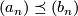 ) whenever there exist positive constants
) whenever there exist positive constants  and
and  such that the inequalities
such that the inequalities
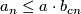
hold for all 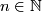 . We say that types of growth
of our sequences
. We say that types of growth
of our sequences 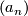 and
and 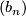 are the same whenever
are the same whenever
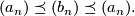
Let now 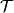 be the set of non-negative increasing functions defined on
be the set of non-negative increasing functions defined on
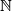 :
:
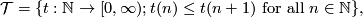
and 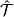 the set of increasing sequences with entries in
the set of increasing sequences with entries in 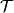 :
:
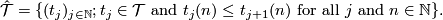
Elements  of
of 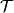 can be identified with sequences
can be identified with sequences 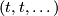 , so
, so
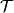 can be considered as a subset of
can be considered as a subset of 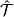 .
.
A preorder  defined by the condition:
defined by the condition:
(*) 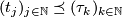 if and only
if there exists
if and only
if there exists 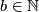 such that for all
such that for all 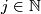 the inequalities
the inequalities
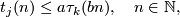
induces an equivalence relation 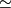 in
in 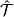 :
:
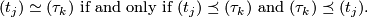
In particular, if  and
and 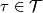 , then
, then
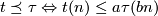
and
![\displaystyle t\simeq\tau\Leftrightarrow a^{-1}\tau ([n/b] )\le t(n)\le a\tau (bn)](/images/math/3/9/9/39920075762460750ebcb56e656ecd68.png)
for all 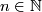 and some
and some 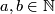 . (Here,
. (Here, ![[x]](/images/math/f/8/d/f8d486cee86578cfe4fddaf090863ff4.png) is the largest
integer which does not exceed
is the largest
integer which does not exceed  ,
, 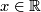 .)
.)
Definition 4.1. Elements of the quotient 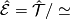 are called
growth types. The growth type of
are called
growth types. The growth type of 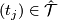 (resp., of
(resp., of 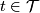 ) is denoted by
) is denoted by ![[(t_j)]](/images/math/9/3/2/9322d2bc60ea96c7550739c46a968a79.png) (resp., by
(resp., by ![[t]](/images/math/a/f/e/afe39aa48eb1ca7f242755040e1b2fec.png) ). Also,
we let
). Also,
we let ![\mathcal{E} = \{ [t];\, t\in\mathcal{T}\}](/images/math/5/f/8/5f8fa4f7ec18b28a4fae049c59f1a1b0.png) .
. 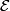 is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
 induces a partial order (denoted again by
induces a partial order (denoted again by  ) in
) in
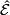 .
.
Example 4.2. ![[0]\preceq [1]\preceq [\log n]\preceq [n]\preceq [n^2]\preceq\dots\preceq [(1, n, n^2, \dots )]\preceq [2^n]\preceq [(1, 2^n, 3^n,\dots )]](/images/math/0/4/6/0466454f7d5dc21e535bfea48de683d1.png) and all the growth types listed above are different. The growth
type of any polynomial of degree
and all the growth types listed above are different. The growth
type of any polynomial of degree 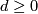 is equal to
is equal to ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) and is called
polynomial (of degree
and is called
polynomial (of degree  ).
). ![[a^n] = [e^n]](/images/math/6/a/a/6aa95a87bcd7ec3c9ae9a43d67a43db7.png) for any
for any  and this growth type is called exponential.
and this growth type is called exponential.
4.1 Growth in groups
For most of results listed here we refer to [Hector&Hirsch1981].
Let  be a finitely generated group and
be a finitely generated group and 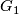 a finite symmetric
(i.e. such that
a finite symmetric
(i.e. such that 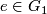 and
and 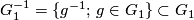 )
set generating it. For any
)
set generating it. For any 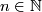 let
let
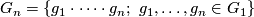
and
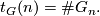
The type of growth of 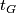 does not depend on
does not depend on 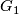 , so we may write the following.
, so we may write the following.
Definition 4.3. The growth type
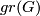 of
of  is defined as
is defined as ![[t_G]](/images/math/e/d/0/ed0a8200ade2d557c1f80768b8aeed7e.png) for any finite symmetric generating set
for any finite symmetric generating set 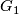 . If
. If  acts on a space
acts on a space  and
and 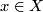 , then the growth type
, then the growth type 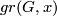 of
of  at
at  is defined in a similar way:
is defined in a similar way: ![gr (G,x) = [t_x]](/images/math/e/b/4/eb46244165e9f374642fba6efe2cbf30.png) , where
, where
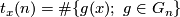
for any fixed finite symmetric generating set 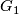 .
.
Example 4.4. A finite group has the growth type ![[1]](/images/math/e/f/1/ef1046ca56d6240cc302cb4a5fdb301c.png) while the
abelian group
while the
abelian group 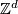 has the polynomial growth of degree
has the polynomial growth of degree  . Any free
(non-abelian) group has the exponential growth
. Any free
(non-abelian) group has the exponential growth ![[e^n]](/images/math/3/a/6/3a6f983ab43d8e3f848fab287b391a56.png) .
.
Proposition 4.5. For any finitely generated group  and
any normal subgroup
and
any normal subgroup  of
of  we have
we have ![gr (G/H)\preceq gr (G)\preceq [e^n].](/images/math/0/2/e/02ee95d5b465acf28e785980f448a21e.png)
Proposition 4.6. Any finitely generated abelian group of rank  has the growth type
has the growth type ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) .
.
Theorem 4.7. Any finitely generated nilpotent group is of polynomial type of growth. Moreover, if a finitely generated group contains a nilpotent group of finite index, then it has a polynomial type of growth [Wolf1968]. Conversely, any finitely generated group of polynomial type of growth contains a nilpotent subgroup of finite index [Gromov1981].
Natural examples of finitely generated groups are provided by
fundamental groups of compact manifolds. Below we show how the growth type
of the fundamental group of a compact Riemannian manifold is related to
its geometry. To this end let us consider a
complete Riemannian manifold  , fix a point
, fix a point 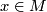 and let
and let
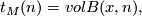
where 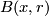 is the ball on
is the ball on  of radius
of radius  and centre
and centre  while
while 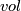 is the measure on
is the measure on  induced by the Riemannian structure. If
induced by the Riemannian structure. If 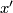 is another point of
is another point of  , then
, then 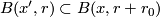 , where
, where 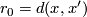 and
and  is the distance function on
is the distance function on  .
Therefore, the following definition is correct.
.
Therefore, the following definition is correct.
Definition 4.8. ![gr (M) = [t_M]](/images/math/0/5/d/05db23e360caae209afbf3bf0b30fc43.png) is called the growth type of a Riemannian manifold
is called the growth type of a Riemannian manifold  .
.
Proposition 4.9 ([Milnor1968a], [Švarc1955]). If  is compact, then the fundamental group
is compact, then the fundamental group 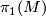 and the universal covering
and the universal covering 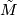 of
of  have the same growth type. If
have the same growth type. If  is a compact Riemannian manifold of negative sectional
curvature, then both
is a compact Riemannian manifold of negative sectional
curvature, then both 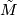 and
and 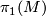 have exponential growth.
have exponential growth.
Fundamental groups of compact manifolds of negative sectional curvature are hyperbolic in the sense of [Gromov1987]. The last statement of the Proposition above can be generalized as follows,
Proposition 4.10. Any non-elementary hyperbolic group has exponential growth.
4.2 Orbit growth in pseudogroups
4.3 Expansion growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Gromov1981] M. Gromov, Groups of polynomial growth and expanding maps, Inst. Hautes Études Sci. Publ. Math. (1981), no.53, 53–73. MR623534 (83b:53041) Zbl 0474.20018
- [Gromov1987] M. Gromov, Hyperbolic groups, Essays in group theory,Math. Sci. Res. Inst. Publ., 8, Springer, New York, (1987) 75–263. MR0919829 (89e:20070) Zbl 0634.20015
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Hector&Hirsch1981] G. Hector and U. Hirsch, Introduction to the geometry of foliations. Part A, Friedr. Vieweg \& Sohn, Braunschweig, 1981. MR639738 (83d:57019) Zbl 0628.57001
- [Milnor1968a] J. Milnor, A note on curvature and fundamental group, J. Differential Geometry 2 (1968), 1–7. MR0232311 (38 #636) Zbl 0162.25401
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022
- [Wolf1968] J. A. Wolf, Growth of finitely generated solvable groups and curvature of Riemanniann manifolds, J. Differential Geometry 2 (1968), 421–446. MR0248688 (40 #1939) Zbl 0207.51803
- [Švarc1955] A. S. Švarc, A volume invariant of coverings, Dokl. Akad. Nauk SSSR (N.S.) 105 (1955), 32–34. MR0075634 (17,781d)
 consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo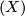 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 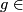 Homeo
Homeo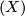 , then
, then
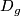 is its domain and
is its domain and 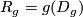 .
.
Definition 2.1.
A subfamily  of Homeo
of Homeo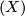 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,  should satisfy the following conditions:
should satisfy the following conditions:
(i) 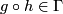 whenever
whenever  and
and 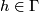 ,
,
(ii) 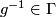 whenever
whenever 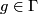 ,
,
(iii) 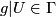 whenever
whenever 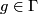 and
and 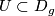 is
open,
is
open,
(iv) if 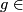 Homeo
Homeo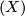 ,
, 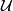 is an open cover of
is an open cover of 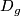 and
and
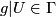 for any
for any 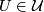 , then
, then 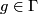 .
.
Moreover, we shall always assume that
(v] id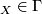 (or, equivalently,
(or, equivalently, 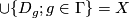 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 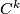 ,
, 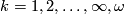 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 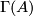 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 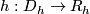 belongs to
belongs to 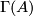 if and only if for any point
if and only if for any point 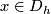 there exist elements
there exist elements 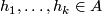 , exponents
, exponents 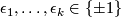 and a neighbourhood
and a neighbourhood  of
of  such that
such that 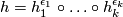 on
on  . If
. If  is finite,
is finite, 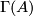 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 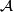 on a foliated manifold
on a foliated manifold 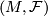 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 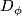 of the charts
of the charts 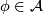 ) if
) if
(i) the covering 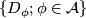 is locally finite,
is locally finite,
(ii) for any 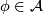 ,
, 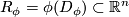 is an open cube,
is an open cube,
(iii) if 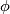 and
and 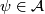 , and
, and 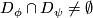 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 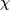 and such that
and such that
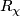 is an open cube,
is an open cube, 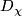 contains the closure of
contains the closure of 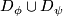 and
and 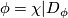 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 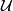 of a foliated manifold
of a foliated manifold 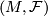 . For
any
. For
any 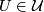 , let
, let 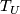 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 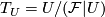 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 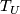 is homeomorphic
(
is homeomorphic
(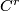 -diffeomorphic when
-diffeomorphic when  is
is 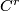 -differentiable and
-differentiable and 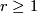 ) to an
open cube
) to an
open cube 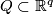 (
(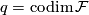 ) via the map
) via the map
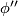 , where
, where 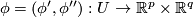 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
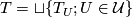
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class 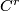 ,
,  , each of the spaces
, each of the spaces 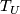 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a 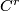 -submanifold
-submanifold 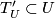 transverse to
transverse to  : if
: if 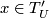 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
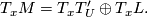
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 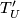 .
.
Definition 3.2. Given a nice covering 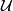 of a foliated manifold
of a foliated manifold 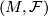 and two sets
and two sets  and
and 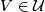 such that
such that 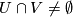 the holonomy map
the holonomy map 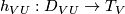 ,
,
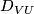 being the open subset of
being the open subset of 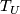 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 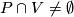 , is defined in the following
way:
, is defined in the following
way:
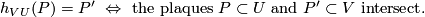
All the maps 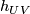 (
(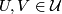 ) generate a pseudogroup
) generate a pseudogroup 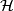 on
on  .
.
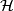 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 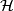 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 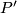 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 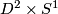 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 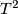 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 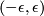 (
( ), the point of intersection
), the point of intersection 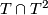 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 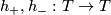 such that
such that 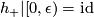 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 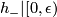 contract their domains towards
contract their domains towards  .
.
4 Growth
Let us begin with two non-decreasing sequences 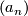 and
and 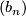 of
non-negative numbers. We shall say that
of
non-negative numbers. We shall say that 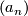 "grows slower" that
"grows slower" that
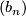 (
(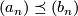 ) whenever there exist positive constants
) whenever there exist positive constants  and
and  such that the inequalities
such that the inequalities
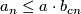
hold for all 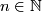 . We say that types of growth
of our sequences
. We say that types of growth
of our sequences 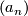 and
and 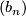 are the same whenever
are the same whenever
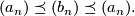
Let now 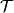 be the set of non-negative increasing functions defined on
be the set of non-negative increasing functions defined on
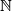 :
:
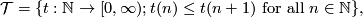
and 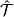 the set of increasing sequences with entries in
the set of increasing sequences with entries in 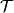 :
:
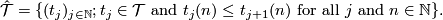
Elements  of
of 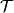 can be identified with sequences
can be identified with sequences 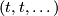 , so
, so
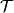 can be considered as a subset of
can be considered as a subset of 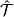 .
.
A preorder  defined by the condition:
defined by the condition:
(*) 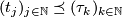 if and only
if there exists
if and only
if there exists 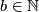 such that for all
such that for all 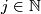 the inequalities
the inequalities
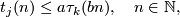
induces an equivalence relation 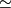 in
in 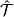 :
:
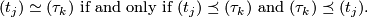
In particular, if  and
and 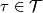 , then
, then
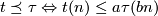
and
![\displaystyle t\simeq\tau\Leftrightarrow a^{-1}\tau ([n/b] )\le t(n)\le a\tau (bn)](/images/math/3/9/9/39920075762460750ebcb56e656ecd68.png)
for all 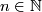 and some
and some 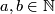 . (Here,
. (Here, ![[x]](/images/math/f/8/d/f8d486cee86578cfe4fddaf090863ff4.png) is the largest
integer which does not exceed
is the largest
integer which does not exceed  ,
, 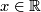 .)
.)
Definition 4.1. Elements of the quotient 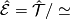 are called
growth types. The growth type of
are called
growth types. The growth type of 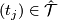 (resp., of
(resp., of 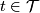 ) is denoted by
) is denoted by ![[(t_j)]](/images/math/9/3/2/9322d2bc60ea96c7550739c46a968a79.png) (resp., by
(resp., by ![[t]](/images/math/a/f/e/afe39aa48eb1ca7f242755040e1b2fec.png) ). Also,
we let
). Also,
we let ![\mathcal{E} = \{ [t];\, t\in\mathcal{T}\}](/images/math/5/f/8/5f8fa4f7ec18b28a4fae049c59f1a1b0.png) .
. 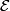 is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
is the set of growth
types of monotone functions (in the sense of [Hector&Hirsch1981]). The preorder
 induces a partial order (denoted again by
induces a partial order (denoted again by  ) in
) in
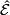 .
.
Example 4.2. ![[0]\preceq [1]\preceq [\log n]\preceq [n]\preceq [n^2]\preceq\dots\preceq [(1, n, n^2, \dots )]\preceq [2^n]\preceq [(1, 2^n, 3^n,\dots )]](/images/math/0/4/6/0466454f7d5dc21e535bfea48de683d1.png) and all the growth types listed above are different. The growth
type of any polynomial of degree
and all the growth types listed above are different. The growth
type of any polynomial of degree 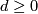 is equal to
is equal to ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) and is called
polynomial (of degree
and is called
polynomial (of degree  ).
). ![[a^n] = [e^n]](/images/math/6/a/a/6aa95a87bcd7ec3c9ae9a43d67a43db7.png) for any
for any  and this growth type is called exponential.
and this growth type is called exponential.
4.1 Growth in groups
For most of results listed here we refer to [Hector&Hirsch1981].
Let  be a finitely generated group and
be a finitely generated group and 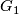 a finite symmetric
(i.e. such that
a finite symmetric
(i.e. such that 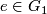 and
and 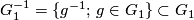 )
set generating it. For any
)
set generating it. For any 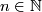 let
let
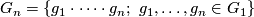
and
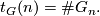
The type of growth of 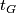 does not depend on
does not depend on 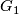 , so we may write the following.
, so we may write the following.
Definition 4.3. The growth type
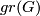 of
of  is defined as
is defined as ![[t_G]](/images/math/e/d/0/ed0a8200ade2d557c1f80768b8aeed7e.png) for any finite symmetric generating set
for any finite symmetric generating set 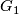 . If
. If  acts on a space
acts on a space  and
and 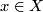 , then the growth type
, then the growth type 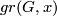 of
of  at
at  is defined in a similar way:
is defined in a similar way: ![gr (G,x) = [t_x]](/images/math/e/b/4/eb46244165e9f374642fba6efe2cbf30.png) , where
, where
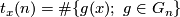
for any fixed finite symmetric generating set 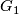 .
.
Example 4.4. A finite group has the growth type ![[1]](/images/math/e/f/1/ef1046ca56d6240cc302cb4a5fdb301c.png) while the
abelian group
while the
abelian group 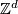 has the polynomial growth of degree
has the polynomial growth of degree  . Any free
(non-abelian) group has the exponential growth
. Any free
(non-abelian) group has the exponential growth ![[e^n]](/images/math/3/a/6/3a6f983ab43d8e3f848fab287b391a56.png) .
.
Proposition 4.5. For any finitely generated group  and
any normal subgroup
and
any normal subgroup  of
of  we have
we have ![gr (G/H)\preceq gr (G)\preceq [e^n].](/images/math/0/2/e/02ee95d5b465acf28e785980f448a21e.png)
Proposition 4.6. Any finitely generated abelian group of rank  has the growth type
has the growth type ![[n^d]](/images/math/2/b/e/2befa1bf181192d8e036bd0ca974af9b.png) .
.
Theorem 4.7. Any finitely generated nilpotent group is of polynomial type of growth. Moreover, if a finitely generated group contains a nilpotent group of finite index, then it has a polynomial type of growth [Wolf1968]. Conversely, any finitely generated group of polynomial type of growth contains a nilpotent subgroup of finite index [Gromov1981].
Natural examples of finitely generated groups are provided by
fundamental groups of compact manifolds. Below we show how the growth type
of the fundamental group of a compact Riemannian manifold is related to
its geometry. To this end let us consider a
complete Riemannian manifold  , fix a point
, fix a point 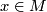 and let
and let
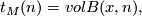
where 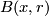 is the ball on
is the ball on  of radius
of radius  and centre
and centre  while
while 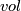 is the measure on
is the measure on  induced by the Riemannian structure. If
induced by the Riemannian structure. If 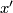 is another point of
is another point of  , then
, then 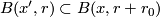 , where
, where 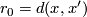 and
and  is the distance function on
is the distance function on  .
Therefore, the following definition is correct.
.
Therefore, the following definition is correct.
Definition 4.8. ![gr (M) = [t_M]](/images/math/0/5/d/05db23e360caae209afbf3bf0b30fc43.png) is called the growth type of a Riemannian manifold
is called the growth type of a Riemannian manifold  .
.
Proposition 4.9 ([Milnor1968a], [Švarc1955]). If  is compact, then the fundamental group
is compact, then the fundamental group 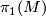 and the universal covering
and the universal covering 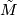 of
of  have the same growth type. If
have the same growth type. If  is a compact Riemannian manifold of negative sectional
curvature, then both
is a compact Riemannian manifold of negative sectional
curvature, then both 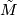 and
and 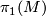 have exponential growth.
have exponential growth.
Fundamental groups of compact manifolds of negative sectional curvature are hyperbolic in the sense of [Gromov1987]. The last statement of the Proposition above can be generalized as follows,
Proposition 4.10. Any non-elementary hyperbolic group has exponential growth.
4.2 Orbit growth in pseudogroups
4.3 Expansion growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Gromov1981] M. Gromov, Groups of polynomial growth and expanding maps, Inst. Hautes Études Sci. Publ. Math. (1981), no.53, 53–73. MR623534 (83b:53041) Zbl 0474.20018
- [Gromov1987] M. Gromov, Hyperbolic groups, Essays in group theory,Math. Sci. Res. Inst. Publ., 8, Springer, New York, (1987) 75–263. MR0919829 (89e:20070) Zbl 0634.20015
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Hector&Hirsch1981] G. Hector and U. Hirsch, Introduction to the geometry of foliations. Part A, Friedr. Vieweg \& Sohn, Braunschweig, 1981. MR639738 (83d:57019) Zbl 0628.57001
- [Milnor1968a] J. Milnor, A note on curvature and fundamental group, J. Differential Geometry 2 (1968), 1–7. MR0232311 (38 #636) Zbl 0162.25401
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022
- [Wolf1968] J. A. Wolf, Growth of finitely generated solvable groups and curvature of Riemanniann manifolds, J. Differential Geometry 2 (1968), 421–446. MR0248688 (40 #1939) Zbl 0207.51803
- [Švarc1955] A. S. Švarc, A volume invariant of coverings, Dokl. Akad. Nauk SSSR (N.S.) 105 (1955), 32–34. MR0075634 (17,781d)