Dold manifold
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A Dold manifold is a manifold of the form
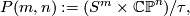
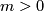 , and the involution
, and the involution  sends
sends ![(x,[y])](/images/math/5/f/4/5f4498f04b89f91ead4518908defc4a5.png) to
to ![(-x, [\bar y])](/images/math/d/b/a/dba628c4f8c13c856cc15d4ca98d20dd.png) where
where 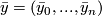 for
for 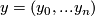 .
.
Dold used these manifolds in [Dold1956] as generators for the unoriented bordism ring.
2 Construction and examples
...
3 Invariants
The fibre bundle 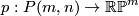 has a section
has a section ![s([x]) := [(x,[1,...,1])]](/images/math/f/0/b/f0bc2e5170189927bc8b9e2c1f82f6ac.png) and we consider the cohomology classes (always with
and we consider the cohomology classes (always with 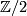 -coefficients)
-coefficients)
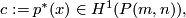
where  is a generator of
is a generator of 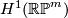 , and
, and
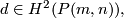
which is characterized by the property that the restriction to a fibre is non-trivial and 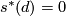 .
.
Theorem [Dold1956] 3.1. The classes 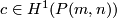 and
and 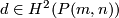 generate
generate 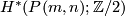 with only the relations
with only the relations
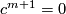
and
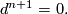
The Steenrod squares act by
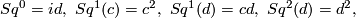
and all other Squares 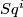 act trivially on
act trivially on  and
and  . On the decomposable classes the action is given by the Cartan formula.
. On the decomposable classes the action is given by the Cartan formula.
The total Stiefel-Whitney class of the tangent bundle is
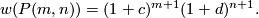
4 Classification/Characterization
...
5 Further discussion
...
6 References
- [Dold1956] A. Dold, Erzeugende der Thomschen Algebra
 , Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
, Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601