Concordance implies isotopy for smooth structures on 3-manifolds?
CarmenRovi (Talk | contribs) |
CarmenRovi (Talk | contribs) (→Problem) |
||
| Line 3: | Line 3: | ||
| − | A $3$-manifold has a smooth structure which is essentially unique. One question is what does | + | A $3$-manifold has a smooth structure which is essentially unique. One question is what does "essentially unique" mean. |
| − | In high dimensions | + | In high dimensions, smooth structures can be classified either up to concordance or up to isotopy. In high dimensions concordance implies isotopy. |
| − | + | Let $M^n$ be a topological manifold and let $W^{n+1}$ be a smooth manifold homeomorphic to $M \times I$, one can ask if that smooth manifold $W$ is diffeomorphic to a product, | |
$$W \xrightarrow{diffeo} \partial_+ W \times I$$ | $$W \xrightarrow{diffeo} \partial_+ W \times I$$ | ||
| − | + | This "concordance implies isotopy" theorem of Kirby-Siebenmann and Hirsch is: | |
| − | This | + | |
\begin{itemize} | \begin{itemize} | ||
\item true in high dimensions, $n \geq 5$. | \item true in high dimensions, $n \geq 5$. | ||
Revision as of 07:11, 8 January 2019
1 Problem
A  -manifold has a smooth structure which is essentially unique. One question is what does "essentially unique" mean.
-manifold has a smooth structure which is essentially unique. One question is what does "essentially unique" mean.
In high dimensions, smooth structures can be classified either up to concordance or up to isotopy. In high dimensions concordance implies isotopy.
Let 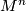 be a topological manifold and let
be a topological manifold and let 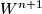 be a smooth manifold homeomorphic to
be a smooth manifold homeomorphic to 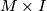 , one can ask if that smooth manifold
, one can ask if that smooth manifold  is diffeomorphic to a product,
is diffeomorphic to a product,
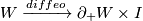
This "concordance implies isotopy" theorem of Kirby-Siebenmann and Hirsch is:
\begin{itemize}
\item true in high dimensions,  .
.
If you have a topological manifold 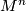 , you can classify smooth structures as homotopy classes of maps
, you can classify smooth structures as homotopy classes of maps
![\displaystyle \mathcal{S}^{TOP/O}(M^n) = [M^n, TOP/O]](/images/math/5/2/3/523c667c682f66d0b0022e4422f79140.png)
The structure set 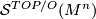 is the set of classes of smoothings on
is the set of classes of smoothings on 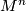 . But it is important to decide what is meant by the ``structure" and there are two possible equivalence relations: concordance or isotopy.
. But it is important to decide what is meant by the ``structure" and there are two possible equivalence relations: concordance or isotopy.
A smoothing is a homeomorphism from a smooth manifold  to
to 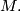

Two smoothings  and
and  are \textit{concordant} if there is a smooth manifold
are \textit{concordant} if there is a smooth manifold 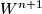 and a homeomorphism to
and a homeomorphism to 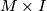 that restricts to these two smoothings.
that restricts to these two smoothings.
\medskip
Two smoothings  and
and  are isotopic if there is a smooth manifold
are isotopic if there is a smooth manifold  and a level-preserving homeomorphism
and a level-preserving homeomorphism 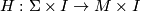 ,
,
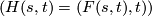
inducing 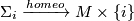 for
for 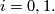
Theorem 1.1. If dim 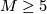 , then concordant structures are isotopic (and hence diffeomorphic).
, then concordant structures are isotopic (and hence diffeomorphic).
\item false for simply-connected  -manifolds by the failure of the
-manifolds by the failure of the  -cobordism theorem. Cappell and Shanneson proved in the non-simply connected case that there are counterexamples to the
-cobordism theorem. Cappell and Shanneson proved in the non-simply connected case that there are counterexamples to the  -cobordism theorem.
\item we don't know the answer for
-cobordism theorem.
\item we don't know the answer for  .
\end{itemize}
.
\end{itemize}
aa