Complete intersections
(→Classification in low dimensions) |
m (→Construction and examples) |
||
| Line 3: | Line 3: | ||
<wikitex>; | <wikitex>; | ||
Let $f_1, \dots, f_k$ be complex, homogeneous polynomials of degree $d_1, \dots, d_k$ in $n+k+1$ complex variables $z = (z_1, \dots, z_{n+k+1})$. Define | Let $f_1, \dots, f_k$ be complex, homogeneous polynomials of degree $d_1, \dots, d_k$ in $n+k+1$ complex variables $z = (z_1, \dots, z_{n+k+1})$. Define | ||
| − | $$ X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} | f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.$$ | + | $$ X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} \,|\, f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.$$ |
The set $X(f_1, \dots f_k)$ is an [[Wikipedia:Algebraic_variety|algebraic variety]]. It is non-singular if for all $j$ with $0 \leq j \leq n+k$ the affine function | The set $X(f_1, \dots f_k)$ is an [[Wikipedia:Algebraic_variety|algebraic variety]]. It is non-singular if for all $j$ with $0 \leq j \leq n+k$ the affine function | ||
$$ \Cc^{n+k} \to \Cc^{k}, ~~~ (z_1, \dots, z_{n+k}) \longmapsto (f_1^j(z_1, \dots, z_{n+k}), \dots, f_k^j(z_1, \dots, z_{n+k}))$$ | $$ \Cc^{n+k} \to \Cc^{k}, ~~~ (z_1, \dots, z_{n+k}) \longmapsto (f_1^j(z_1, \dots, z_{n+k}), \dots, f_k^j(z_1, \dots, z_{n+k}))$$ | ||
Latest revision as of 06:28, 7 January 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Construction and examples
Let 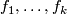 be complex, homogeneous polynomials of degree
be complex, homogeneous polynomials of degree 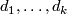 in
in 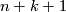 complex variables
complex variables 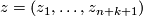 . Define
. Define
![\displaystyle X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} \,|\, f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.](/images/math/7/d/5/7d5c8a6b1074fc313e9208c93629bd44.png)
The set 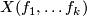 is an algebraic variety. It is non-singular if for all
is an algebraic variety. It is non-singular if for all  with
with 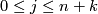 the affine function
the affine function
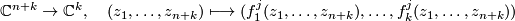
where 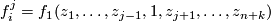 , has
, has  as a regular value. In this case
as a regular value. In this case 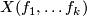 is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension
is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension  . This is called a complete intersection.
. This is called a complete intersection.
By a theorem of Thom [???] the diffeomorphism type of 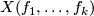 depends only upon the multi-degree,
depends only upon the multi-degree, 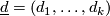 , and we write
, and we write 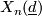 for
for 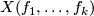 .
.
For example:
-
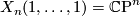 ,
,
-
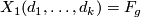 the oriented surface of genus
the oriented surface of genus 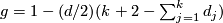 ,
,
-
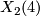 is a complex K3 surface,
is a complex K3 surface,
-
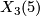 is a Calabi-Yau 3-fold.
is a Calabi-Yau 3-fold.
2 Invariants
By the Lefschetz hyperplane theorem the inclusion 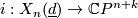 is an n-connected map. Hence:
is an n-connected map. Hence:
- if n > 1 then
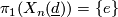 ,
,
-
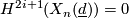 if
if 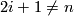 ,
,
-
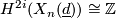 for all
for all 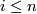 unless
unless 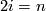 .
.
-
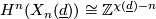 where
where 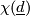 is the Euler characteristic of
is the Euler characteristic of 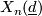 which we discuss further below.
which we discuss further below.
- When
 is even
is even 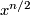 generates a summand of
generates a summand of 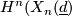 .
.
Note that here and throughout integer coefficients are use for (co)homology.
2.1 Cohomology ring
Let  be the canonical line bundle over
be the canonical line bundle over 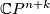 and let
and let 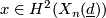 be defined by
be defined by 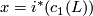 where
where 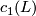 is the first Chern class of
is the first Chern class of  . Let
. Let
![[X_n({\underline{d}})] \in H_{2n}(X_n({\underline{d}}))](/images/math/f/4/2/f4299a7fd070d25d25a2a0cd434e0c6a.png) denote the fundamental class of
denote the fundamental class of 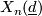 and let
and let 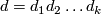 be the product of all degrees, called the total degree. We have the following useful identity [???]
be the product of all degrees, called the total degree. We have the following useful identity [???]
![\displaystyle \langle x^n, [X_n({\underline{d}})] \rangle = d.](/images/math/c/4/2/c42040a33bb3081f0d64c0ef9cba1e3b.png)
Let 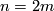 or
or 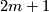 and consider the graded ring
and consider the graded ring
![\displaystyle H^*(n, d) :=\Zz[x, y]/\{x^{m+1} = dy, y^2 = 0 \}](/images/math/a/2/8/a2875558e0fa4f20ba7f73dbf2170c41.png)
where the dimensions of  and
and  are
are  and
and 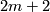 respectively. Let
respectively. Let 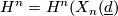 , considered as a graded ring in dimension
, considered as a graded ring in dimension 
- If
 is odd:
is odd:
- the ring
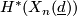 is determined by
is determined by  ,
,  and
and 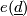 ,
,
- there is a short exact sequence
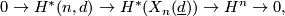
- the intersection form
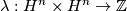 is of course skew hyperbolic.
is of course skew hyperbolic.
- the ring
- If
 is even:
is even:
- the ring
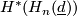 is determined by
is determined by  ,
,  and the pair
and the pair 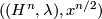 :
:
- there is a short exact sequence
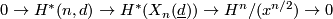 .
.
- Some properties of
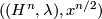 are described below.
are described below.
- the ring
Proposition 2.1 [Libgober&Wood1981].
If  is even, then
is even, then 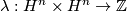 is indefinite unless
is indefinite unless 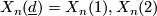 or
or 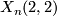 .
.
2.2 Characteristic classes
The stable tangent bundle of 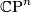 is isomorphic to
is isomorphic to 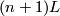 , [Milnor&Stasheff1974], and the normal bundle of the inclusion
, [Milnor&Stasheff1974], and the normal bundle of the inclusion 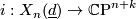 is given by the identity [???]
is given by the identity [???]
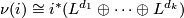
where 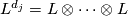 denotes the
denotes the 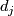 -fold tensor product of
-fold tensor product of  with itself. From this one deduces that the stable tangent bundle of
with itself. From this one deduces that the stable tangent bundle of 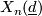 ,
, 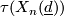 , satisfies the equation
, satisfies the equation
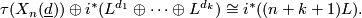
It follows immediately that the total Chern class and the total Pontrjagin class of 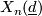 are given by
are given by
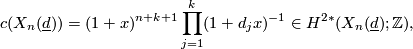
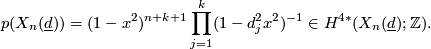
Moreover, the Euler class and Euler characteristic of 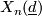 is given by
is given by
![\displaystyle e(X_n({\underline{d}})) = c_n(X_n({\underline{d}})), ~~~ \chi(\underline{d}) = \langle e(X_n(\underline{d}), [X_n(\underline{d})]\rangle.](/images/math/f/e/0/fe059d8703b858339f44a160448043ea.png)
3 Classification
The smooth classification of complete intersections for 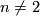 is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
Conjecture 3.1. For 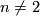 , complete intersections
, complete intersections 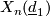 and
and 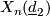 are diffeomorphic if and only if all of the following conditions hold
are diffeomorphic if and only if all of the following conditions hold
-
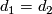 ,
,
-
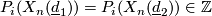 ,
,
-
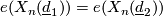 .
.
Note that we regard 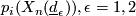 as multiplies of
as multiplies of 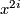 in order to view
in order to view 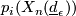 as an element of
as an element of  .
.
3.1 Classification in low dimensions
- For
 the Sullivan Conjecture holds by the classification of surfaces.
the Sullivan Conjecture holds by the classification of surfaces.
- For
 the topological Sullivan Conjecture holds for
the topological Sullivan Conjecture holds for  by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
- For
 the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
- For
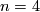 the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
- For
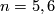 and
and  the topological Sullivan Conjecture is true [Fang&Wang2009].
the topological Sullivan Conjecture is true [Fang&Wang2009].
3.2 Further classification theorems
We now discuss further classification results for complete intersections. Let 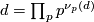 where
where  is prime.
is prime.
Theorem 3.2 [Traving1985].
If  and
and 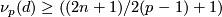 for all
for all  such that
such that 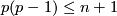 then the Sullivan Conjecture holds.
then the Sullivan Conjecture holds.
Traving's proof uses modified surgery: see [Kreck1999, Section 8] for a summary.
Theorem 3.3 [Fang1997].
If  and
and 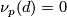 for all
for all  such that
such that 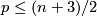 then the topological Sullivan Conjecture holds.
then the topological Sullivan Conjecture holds.
Fang's proof proceeds by extending results of [Libgober&Wood1982] on the homotopy classification of complete intersections where  is even to the case of
is even to the case of  odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
Theorem 3.4 [Fang1997].
Let  and
and  be homotopy equivalent complete intersections. If
be homotopy equivalent complete intersections. If  is odd and
is odd and 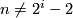 for all
for all 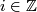 then
then  and
and  are homeomorphic to each other if and only if their Pontrjagin classes agree.
are homeomorphic to each other if and only if their Pontrjagin classes agree.
3.3 Classification up to homotopy
Recall that the signature of, 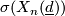 , of
, of 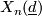 is the signature of its intersection form. If
is the signature of its intersection form. If  is odd
is odd 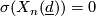 and if
and if  is even
is even 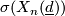 can be computed from the
can be computed from the 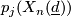 via Hirzebruch's signature theorem.
via Hirzebruch's signature theorem.
Theorem 3.5 [Libgober&Wood1982] and [Fang1997]. Let  and
and  be complete intersections with the same total degree
be complete intersections with the same total degree  . Suppose that
. Suppose that 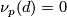 if
if 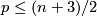 . If
. If 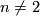 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteristic.
are homotopy equivalent if and only if they have the same signature and Euler characteristic.
Finally we summarise theorems of [Astey&Gitler&Micha&Pastor2003]. Define 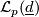 to be the unordered sequence
to be the unordered sequence

obtained by removing entries where 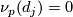 and write
and write  if
if 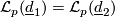 for all primes
for all primes  .
.
Theorem 3.6 [Astey&Gitler&Micha&Pastor2003].
If  and
and 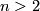 then
then  is homotopy equivalent to
is homotopy equivalent to  if and only if they have the same Euler characteristic and signature.
if and only if they have the same Euler characteristic and signature.
In contrast to the results of Fang and Ligober and Wood which hold when  is small relative to the primes dividing
is small relative to the primes dividing  , the above theorem leads to a homotopy classification which holds when
, the above theorem leads to a homotopy classification which holds when  is large relative to
is large relative to  . If
. If 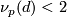 for all p then define
for all p then define 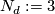 otherwise let
otherwise let
![\displaystyle N_d := \mathrm{Max} \{ 2(p_i-1)p_i^{[(\nu_{p}(d)-2)/2]} | \nu_{p}(d) \geq 2 \}.](/images/math/6/3/6/636ce5ebc2851f61f05adf3e72d0c8ec.png)
Theorem 3.7 [Astey&Gitler&Micha&Pastor2003].
If  and
and  have the same multidegree
have the same multidegree  and
and 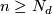 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteritic.
are homotopy equivalent if and only if they have the same signature and Euler characteritic.
4 Further discussion
Conjecture 4.1 Hartshorne. Every smooth algebraic variety of dimension n which is embedded in 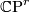 is isomorphic to a complete intersection, if
is isomorphic to a complete intersection, if 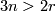 .
.
4.1 Splitting theorems
5 References
- [???] Template:???
- [Astey&Gitler&Micha&Pastor2003] L. Astey, S. Gitler, E. Micha and G. Pastor, On the homotopy type of complete intersections, Topology 44 (2005), no.1, 249–260. MR2104011 (2005i:14058) Zbl 1072.14063
- [Ebeling1990] W. Ebeling, An example of two homeomorphic, nondiffeomorphic complete intersection surfaces, Invent. Math. 99 (1990), no.3, 651–654. MR1032884 (91c:57038) Zbl 0707.14045
- [Fang&Klaus1996] F. Fang and S. Klaus, Topological classification of
 -dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
-dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
- [Fang&Wang2009] F. Fang and J. Wang, Homeomorphism classification of complex projective complete intersections of dimensions 5, 6 and 7, to appear in Math. Zeit. (2009).
- [Fang1997] F. Fang, Topology of complete intersections, Comment. Math. Helv. 72 (1997), no.3, 466–480. MR1476060 (98k:14071) Zbl 0896.14028
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Libgober&Wood1981] A. S. Libgober and J. W. Wood, On the topological structure of even-dimensional complete intersections, Trans. Amer. Math. Soc. 267 (1981), no.2, 637–660. MR626495 (83e:57017) Zbl 0475.57013
- [Libgober&Wood1982] A. S. Libgober and J. W. Wood, Differentiable structures on complete intersections. I, Topology 21 (1982), no.4, 469–482. MR670748 (84a:57037) Zbl 0504.57015
- [Libgober&Wood1990] A. S. Libgober and J. W. Wood, Uniqueness of the complex structure on Kähler manifolds of certain homotopy types, J. Differential Geom. 32 (1990), no.1, 139–154. MR1064869 (91g:32039) Zbl 0711.53052
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Traving1985] C. Traving, Zur Diffeomorphieklassifikation vollständiger Durchschnitte, Diplomarbeit, Mainz (1985).
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
6 External links
- The Wikipedia page about complete intersections
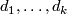 in
in 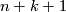 complex variables
complex variables 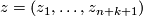 . Define
. Define
![\displaystyle X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} \,|\, f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.](/images/math/7/d/5/7d5c8a6b1074fc313e9208c93629bd44.png)
The set 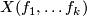 is an algebraic variety. It is non-singular if for all
is an algebraic variety. It is non-singular if for all  with
with 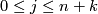 the affine function
the affine function
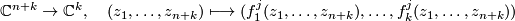
where 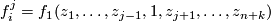 , has
, has  as a regular value. In this case
as a regular value. In this case 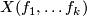 is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension
is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension  . This is called a complete intersection.
. This is called a complete intersection.
By a theorem of Thom [???] the diffeomorphism type of 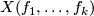 depends only upon the multi-degree,
depends only upon the multi-degree, 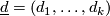 , and we write
, and we write 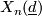 for
for 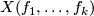 .
.
For example:
-
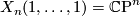 ,
,
-
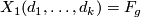 the oriented surface of genus
the oriented surface of genus 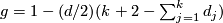 ,
,
-
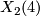 is a complex K3 surface,
is a complex K3 surface,
-
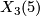 is a Calabi-Yau 3-fold.
is a Calabi-Yau 3-fold.
2 Invariants
By the Lefschetz hyperplane theorem the inclusion 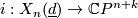 is an n-connected map. Hence:
is an n-connected map. Hence:
- if n > 1 then
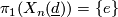 ,
,
-
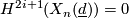 if
if 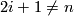 ,
,
-
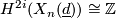 for all
for all 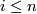 unless
unless 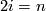 .
.
-
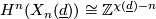 where
where 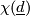 is the Euler characteristic of
is the Euler characteristic of 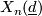 which we discuss further below.
which we discuss further below.
- When
 is even
is even 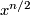 generates a summand of
generates a summand of 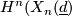 .
.
Note that here and throughout integer coefficients are use for (co)homology.
2.1 Cohomology ring
Let  be the canonical line bundle over
be the canonical line bundle over 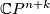 and let
and let 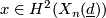 be defined by
be defined by 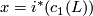 where
where 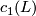 is the first Chern class of
is the first Chern class of  . Let
. Let
![[X_n({\underline{d}})] \in H_{2n}(X_n({\underline{d}}))](/images/math/f/4/2/f4299a7fd070d25d25a2a0cd434e0c6a.png) denote the fundamental class of
denote the fundamental class of 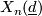 and let
and let 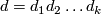 be the product of all degrees, called the total degree. We have the following useful identity [???]
be the product of all degrees, called the total degree. We have the following useful identity [???]
![\displaystyle \langle x^n, [X_n({\underline{d}})] \rangle = d.](/images/math/c/4/2/c42040a33bb3081f0d64c0ef9cba1e3b.png)
Let 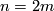 or
or 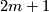 and consider the graded ring
and consider the graded ring
![\displaystyle H^*(n, d) :=\Zz[x, y]/\{x^{m+1} = dy, y^2 = 0 \}](/images/math/a/2/8/a2875558e0fa4f20ba7f73dbf2170c41.png)
where the dimensions of  and
and  are
are  and
and 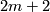 respectively. Let
respectively. Let 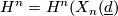 , considered as a graded ring in dimension
, considered as a graded ring in dimension 
- If
 is odd:
is odd:
- the ring
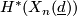 is determined by
is determined by  ,
,  and
and 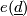 ,
,
- there is a short exact sequence
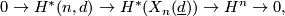
- the intersection form
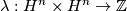 is of course skew hyperbolic.
is of course skew hyperbolic.
- the ring
- If
 is even:
is even:
- the ring
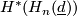 is determined by
is determined by  ,
,  and the pair
and the pair 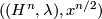 :
:
- there is a short exact sequence
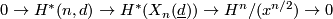 .
.
- Some properties of
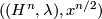 are described below.
are described below.
- the ring
Proposition 2.1 [Libgober&Wood1981].
If  is even, then
is even, then 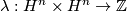 is indefinite unless
is indefinite unless 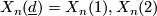 or
or 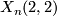 .
.
2.2 Characteristic classes
The stable tangent bundle of 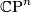 is isomorphic to
is isomorphic to 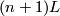 , [Milnor&Stasheff1974], and the normal bundle of the inclusion
, [Milnor&Stasheff1974], and the normal bundle of the inclusion 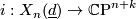 is given by the identity [???]
is given by the identity [???]
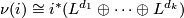
where 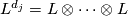 denotes the
denotes the 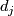 -fold tensor product of
-fold tensor product of  with itself. From this one deduces that the stable tangent bundle of
with itself. From this one deduces that the stable tangent bundle of 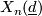 ,
, 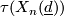 , satisfies the equation
, satisfies the equation
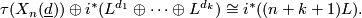
It follows immediately that the total Chern class and the total Pontrjagin class of 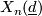 are given by
are given by
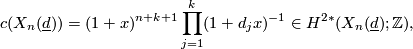
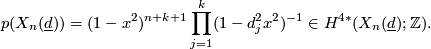
Moreover, the Euler class and Euler characteristic of 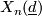 is given by
is given by
![\displaystyle e(X_n({\underline{d}})) = c_n(X_n({\underline{d}})), ~~~ \chi(\underline{d}) = \langle e(X_n(\underline{d}), [X_n(\underline{d})]\rangle.](/images/math/f/e/0/fe059d8703b858339f44a160448043ea.png)
3 Classification
The smooth classification of complete intersections for 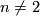 is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
Conjecture 3.1. For 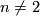 , complete intersections
, complete intersections 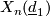 and
and 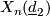 are diffeomorphic if and only if all of the following conditions hold
are diffeomorphic if and only if all of the following conditions hold
-
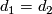 ,
,
-
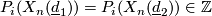 ,
,
-
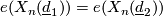 .
.
Note that we regard 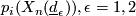 as multiplies of
as multiplies of 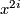 in order to view
in order to view 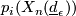 as an element of
as an element of  .
.
3.1 Classification in low dimensions
- For
 the Sullivan Conjecture holds by the classification of surfaces.
the Sullivan Conjecture holds by the classification of surfaces.
- For
 the topological Sullivan Conjecture holds for
the topological Sullivan Conjecture holds for  by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
- For
 the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
- For
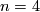 the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
- For
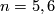 and
and  the topological Sullivan Conjecture is true [Fang&Wang2009].
the topological Sullivan Conjecture is true [Fang&Wang2009].
3.2 Further classification theorems
We now discuss further classification results for complete intersections. Let 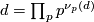 where
where  is prime.
is prime.
Theorem 3.2 [Traving1985].
If  and
and 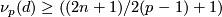 for all
for all  such that
such that 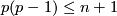 then the Sullivan Conjecture holds.
then the Sullivan Conjecture holds.
Traving's proof uses modified surgery: see [Kreck1999, Section 8] for a summary.
Theorem 3.3 [Fang1997].
If  and
and 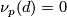 for all
for all  such that
such that 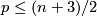 then the topological Sullivan Conjecture holds.
then the topological Sullivan Conjecture holds.
Fang's proof proceeds by extending results of [Libgober&Wood1982] on the homotopy classification of complete intersections where  is even to the case of
is even to the case of  odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
Theorem 3.4 [Fang1997].
Let  and
and  be homotopy equivalent complete intersections. If
be homotopy equivalent complete intersections. If  is odd and
is odd and 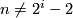 for all
for all 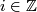 then
then  and
and  are homeomorphic to each other if and only if their Pontrjagin classes agree.
are homeomorphic to each other if and only if their Pontrjagin classes agree.
3.3 Classification up to homotopy
Recall that the signature of, 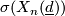 , of
, of 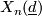 is the signature of its intersection form. If
is the signature of its intersection form. If  is odd
is odd 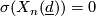 and if
and if  is even
is even 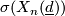 can be computed from the
can be computed from the 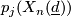 via Hirzebruch's signature theorem.
via Hirzebruch's signature theorem.
Theorem 3.5 [Libgober&Wood1982] and [Fang1997]. Let  and
and  be complete intersections with the same total degree
be complete intersections with the same total degree  . Suppose that
. Suppose that 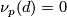 if
if 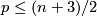 . If
. If 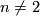 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteristic.
are homotopy equivalent if and only if they have the same signature and Euler characteristic.
Finally we summarise theorems of [Astey&Gitler&Micha&Pastor2003]. Define 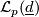 to be the unordered sequence
to be the unordered sequence

obtained by removing entries where 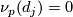 and write
and write  if
if 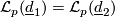 for all primes
for all primes  .
.
Theorem 3.6 [Astey&Gitler&Micha&Pastor2003].
If  and
and 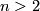 then
then  is homotopy equivalent to
is homotopy equivalent to  if and only if they have the same Euler characteristic and signature.
if and only if they have the same Euler characteristic and signature.
In contrast to the results of Fang and Ligober and Wood which hold when  is small relative to the primes dividing
is small relative to the primes dividing  , the above theorem leads to a homotopy classification which holds when
, the above theorem leads to a homotopy classification which holds when  is large relative to
is large relative to  . If
. If 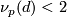 for all p then define
for all p then define 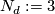 otherwise let
otherwise let
![\displaystyle N_d := \mathrm{Max} \{ 2(p_i-1)p_i^{[(\nu_{p}(d)-2)/2]} | \nu_{p}(d) \geq 2 \}.](/images/math/6/3/6/636ce5ebc2851f61f05adf3e72d0c8ec.png)
Theorem 3.7 [Astey&Gitler&Micha&Pastor2003].
If  and
and  have the same multidegree
have the same multidegree  and
and 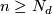 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteritic.
are homotopy equivalent if and only if they have the same signature and Euler characteritic.
4 Further discussion
Conjecture 4.1 Hartshorne. Every smooth algebraic variety of dimension n which is embedded in 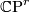 is isomorphic to a complete intersection, if
is isomorphic to a complete intersection, if 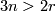 .
.
4.1 Splitting theorems
5 References
- [???] Template:???
- [Astey&Gitler&Micha&Pastor2003] L. Astey, S. Gitler, E. Micha and G. Pastor, On the homotopy type of complete intersections, Topology 44 (2005), no.1, 249–260. MR2104011 (2005i:14058) Zbl 1072.14063
- [Ebeling1990] W. Ebeling, An example of two homeomorphic, nondiffeomorphic complete intersection surfaces, Invent. Math. 99 (1990), no.3, 651–654. MR1032884 (91c:57038) Zbl 0707.14045
- [Fang&Klaus1996] F. Fang and S. Klaus, Topological classification of
 -dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
-dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
- [Fang&Wang2009] F. Fang and J. Wang, Homeomorphism classification of complex projective complete intersections of dimensions 5, 6 and 7, to appear in Math. Zeit. (2009).
- [Fang1997] F. Fang, Topology of complete intersections, Comment. Math. Helv. 72 (1997), no.3, 466–480. MR1476060 (98k:14071) Zbl 0896.14028
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Libgober&Wood1981] A. S. Libgober and J. W. Wood, On the topological structure of even-dimensional complete intersections, Trans. Amer. Math. Soc. 267 (1981), no.2, 637–660. MR626495 (83e:57017) Zbl 0475.57013
- [Libgober&Wood1982] A. S. Libgober and J. W. Wood, Differentiable structures on complete intersections. I, Topology 21 (1982), no.4, 469–482. MR670748 (84a:57037) Zbl 0504.57015
- [Libgober&Wood1990] A. S. Libgober and J. W. Wood, Uniqueness of the complex structure on Kähler manifolds of certain homotopy types, J. Differential Geom. 32 (1990), no.1, 139–154. MR1064869 (91g:32039) Zbl 0711.53052
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Traving1985] C. Traving, Zur Diffeomorphieklassifikation vollständiger Durchschnitte, Diplomarbeit, Mainz (1985).
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
6 External links
- The Wikipedia page about complete intersections
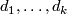 in
in 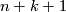 complex variables
complex variables 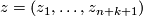 . Define
. Define
![\displaystyle X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} \,|\, f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.](/images/math/7/d/5/7d5c8a6b1074fc313e9208c93629bd44.png)
The set 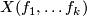 is an algebraic variety. It is non-singular if for all
is an algebraic variety. It is non-singular if for all  with
with 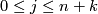 the affine function
the affine function
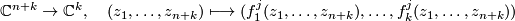
where 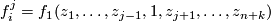 , has
, has  as a regular value. In this case
as a regular value. In this case 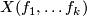 is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension
is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension  . This is called a complete intersection.
. This is called a complete intersection.
By a theorem of Thom [???] the diffeomorphism type of 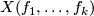 depends only upon the multi-degree,
depends only upon the multi-degree, 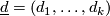 , and we write
, and we write 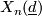 for
for 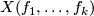 .
.
For example:
-
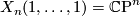 ,
,
-
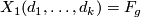 the oriented surface of genus
the oriented surface of genus 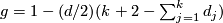 ,
,
-
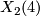 is a complex K3 surface,
is a complex K3 surface,
-
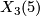 is a Calabi-Yau 3-fold.
is a Calabi-Yau 3-fold.
2 Invariants
By the Lefschetz hyperplane theorem the inclusion 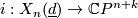 is an n-connected map. Hence:
is an n-connected map. Hence:
- if n > 1 then
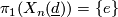 ,
,
-
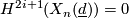 if
if 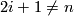 ,
,
-
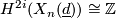 for all
for all 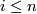 unless
unless 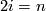 .
.
-
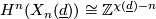 where
where 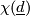 is the Euler characteristic of
is the Euler characteristic of 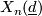 which we discuss further below.
which we discuss further below.
- When
 is even
is even 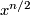 generates a summand of
generates a summand of 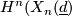 .
.
Note that here and throughout integer coefficients are use for (co)homology.
2.1 Cohomology ring
Let  be the canonical line bundle over
be the canonical line bundle over 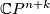 and let
and let 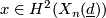 be defined by
be defined by 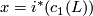 where
where 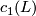 is the first Chern class of
is the first Chern class of  . Let
. Let
![[X_n({\underline{d}})] \in H_{2n}(X_n({\underline{d}}))](/images/math/f/4/2/f4299a7fd070d25d25a2a0cd434e0c6a.png) denote the fundamental class of
denote the fundamental class of 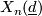 and let
and let 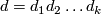 be the product of all degrees, called the total degree. We have the following useful identity [???]
be the product of all degrees, called the total degree. We have the following useful identity [???]
![\displaystyle \langle x^n, [X_n({\underline{d}})] \rangle = d.](/images/math/c/4/2/c42040a33bb3081f0d64c0ef9cba1e3b.png)
Let 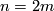 or
or 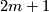 and consider the graded ring
and consider the graded ring
![\displaystyle H^*(n, d) :=\Zz[x, y]/\{x^{m+1} = dy, y^2 = 0 \}](/images/math/a/2/8/a2875558e0fa4f20ba7f73dbf2170c41.png)
where the dimensions of  and
and  are
are  and
and 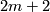 respectively. Let
respectively. Let 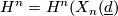 , considered as a graded ring in dimension
, considered as a graded ring in dimension 
- If
 is odd:
is odd:
- the ring
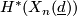 is determined by
is determined by  ,
,  and
and 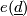 ,
,
- there is a short exact sequence
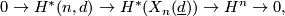
- the intersection form
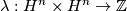 is of course skew hyperbolic.
is of course skew hyperbolic.
- the ring
- If
 is even:
is even:
- the ring
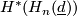 is determined by
is determined by  ,
,  and the pair
and the pair 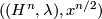 :
:
- there is a short exact sequence
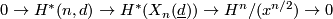 .
.
- Some properties of
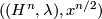 are described below.
are described below.
- the ring
Proposition 2.1 [Libgober&Wood1981].
If  is even, then
is even, then 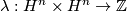 is indefinite unless
is indefinite unless 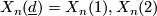 or
or 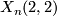 .
.
2.2 Characteristic classes
The stable tangent bundle of 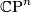 is isomorphic to
is isomorphic to 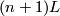 , [Milnor&Stasheff1974], and the normal bundle of the inclusion
, [Milnor&Stasheff1974], and the normal bundle of the inclusion 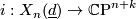 is given by the identity [???]
is given by the identity [???]
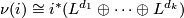
where 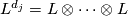 denotes the
denotes the 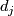 -fold tensor product of
-fold tensor product of  with itself. From this one deduces that the stable tangent bundle of
with itself. From this one deduces that the stable tangent bundle of 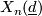 ,
, 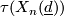 , satisfies the equation
, satisfies the equation
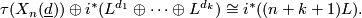
It follows immediately that the total Chern class and the total Pontrjagin class of 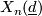 are given by
are given by
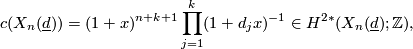
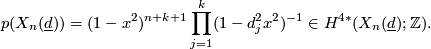
Moreover, the Euler class and Euler characteristic of 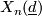 is given by
is given by
![\displaystyle e(X_n({\underline{d}})) = c_n(X_n({\underline{d}})), ~~~ \chi(\underline{d}) = \langle e(X_n(\underline{d}), [X_n(\underline{d})]\rangle.](/images/math/f/e/0/fe059d8703b858339f44a160448043ea.png)
3 Classification
The smooth classification of complete intersections for 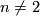 is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
Conjecture 3.1. For 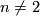 , complete intersections
, complete intersections 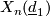 and
and 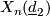 are diffeomorphic if and only if all of the following conditions hold
are diffeomorphic if and only if all of the following conditions hold
-
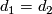 ,
,
-
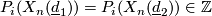 ,
,
-
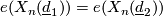 .
.
Note that we regard 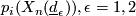 as multiplies of
as multiplies of 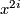 in order to view
in order to view 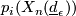 as an element of
as an element of  .
.
3.1 Classification in low dimensions
- For
 the Sullivan Conjecture holds by the classification of surfaces.
the Sullivan Conjecture holds by the classification of surfaces.
- For
 the topological Sullivan Conjecture holds for
the topological Sullivan Conjecture holds for  by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
- For
 the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
- For
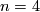 the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
- For
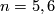 and
and  the topological Sullivan Conjecture is true [Fang&Wang2009].
the topological Sullivan Conjecture is true [Fang&Wang2009].
3.2 Further classification theorems
We now discuss further classification results for complete intersections. Let 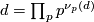 where
where  is prime.
is prime.
Theorem 3.2 [Traving1985].
If  and
and 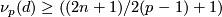 for all
for all  such that
such that 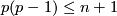 then the Sullivan Conjecture holds.
then the Sullivan Conjecture holds.
Traving's proof uses modified surgery: see [Kreck1999, Section 8] for a summary.
Theorem 3.3 [Fang1997].
If  and
and 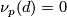 for all
for all  such that
such that 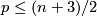 then the topological Sullivan Conjecture holds.
then the topological Sullivan Conjecture holds.
Fang's proof proceeds by extending results of [Libgober&Wood1982] on the homotopy classification of complete intersections where  is even to the case of
is even to the case of  odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
Theorem 3.4 [Fang1997].
Let  and
and  be homotopy equivalent complete intersections. If
be homotopy equivalent complete intersections. If  is odd and
is odd and 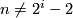 for all
for all 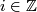 then
then  and
and  are homeomorphic to each other if and only if their Pontrjagin classes agree.
are homeomorphic to each other if and only if their Pontrjagin classes agree.
3.3 Classification up to homotopy
Recall that the signature of, 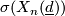 , of
, of 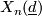 is the signature of its intersection form. If
is the signature of its intersection form. If  is odd
is odd 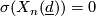 and if
and if  is even
is even 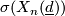 can be computed from the
can be computed from the 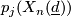 via Hirzebruch's signature theorem.
via Hirzebruch's signature theorem.
Theorem 3.5 [Libgober&Wood1982] and [Fang1997]. Let  and
and  be complete intersections with the same total degree
be complete intersections with the same total degree  . Suppose that
. Suppose that 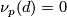 if
if 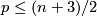 . If
. If 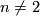 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteristic.
are homotopy equivalent if and only if they have the same signature and Euler characteristic.
Finally we summarise theorems of [Astey&Gitler&Micha&Pastor2003]. Define 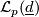 to be the unordered sequence
to be the unordered sequence

obtained by removing entries where 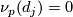 and write
and write  if
if 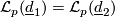 for all primes
for all primes  .
.
Theorem 3.6 [Astey&Gitler&Micha&Pastor2003].
If  and
and 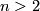 then
then  is homotopy equivalent to
is homotopy equivalent to  if and only if they have the same Euler characteristic and signature.
if and only if they have the same Euler characteristic and signature.
In contrast to the results of Fang and Ligober and Wood which hold when  is small relative to the primes dividing
is small relative to the primes dividing  , the above theorem leads to a homotopy classification which holds when
, the above theorem leads to a homotopy classification which holds when  is large relative to
is large relative to  . If
. If 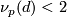 for all p then define
for all p then define 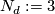 otherwise let
otherwise let
![\displaystyle N_d := \mathrm{Max} \{ 2(p_i-1)p_i^{[(\nu_{p}(d)-2)/2]} | \nu_{p}(d) \geq 2 \}.](/images/math/6/3/6/636ce5ebc2851f61f05adf3e72d0c8ec.png)
Theorem 3.7 [Astey&Gitler&Micha&Pastor2003].
If  and
and  have the same multidegree
have the same multidegree  and
and 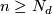 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteritic.
are homotopy equivalent if and only if they have the same signature and Euler characteritic.
4 Further discussion
Conjecture 4.1 Hartshorne. Every smooth algebraic variety of dimension n which is embedded in 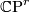 is isomorphic to a complete intersection, if
is isomorphic to a complete intersection, if 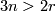 .
.
4.1 Splitting theorems
5 References
- [???] Template:???
- [Astey&Gitler&Micha&Pastor2003] L. Astey, S. Gitler, E. Micha and G. Pastor, On the homotopy type of complete intersections, Topology 44 (2005), no.1, 249–260. MR2104011 (2005i:14058) Zbl 1072.14063
- [Ebeling1990] W. Ebeling, An example of two homeomorphic, nondiffeomorphic complete intersection surfaces, Invent. Math. 99 (1990), no.3, 651–654. MR1032884 (91c:57038) Zbl 0707.14045
- [Fang&Klaus1996] F. Fang and S. Klaus, Topological classification of
 -dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
-dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
- [Fang&Wang2009] F. Fang and J. Wang, Homeomorphism classification of complex projective complete intersections of dimensions 5, 6 and 7, to appear in Math. Zeit. (2009).
- [Fang1997] F. Fang, Topology of complete intersections, Comment. Math. Helv. 72 (1997), no.3, 466–480. MR1476060 (98k:14071) Zbl 0896.14028
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Libgober&Wood1981] A. S. Libgober and J. W. Wood, On the topological structure of even-dimensional complete intersections, Trans. Amer. Math. Soc. 267 (1981), no.2, 637–660. MR626495 (83e:57017) Zbl 0475.57013
- [Libgober&Wood1982] A. S. Libgober and J. W. Wood, Differentiable structures on complete intersections. I, Topology 21 (1982), no.4, 469–482. MR670748 (84a:57037) Zbl 0504.57015
- [Libgober&Wood1990] A. S. Libgober and J. W. Wood, Uniqueness of the complex structure on Kähler manifolds of certain homotopy types, J. Differential Geom. 32 (1990), no.1, 139–154. MR1064869 (91g:32039) Zbl 0711.53052
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Traving1985] C. Traving, Zur Diffeomorphieklassifikation vollständiger Durchschnitte, Diplomarbeit, Mainz (1985).
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
6 External links
- The Wikipedia page about complete intersections
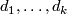 in
in 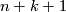 complex variables
complex variables 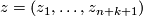 . Define
. Define
![\displaystyle X(f_1, \dots, f_k) \coloneq \{ [z] \in \CP^{n+k} \,|\, f_i(z) = 0 ~\text{for}~ i = 1, \dots, k\}.](/images/math/7/d/5/7d5c8a6b1074fc313e9208c93629bd44.png)
The set 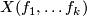 is an algebraic variety. It is non-singular if for all
is an algebraic variety. It is non-singular if for all  with
with 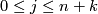 the affine function
the affine function
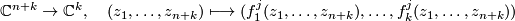
where 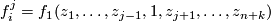 , has
, has  as a regular value. In this case
as a regular value. In this case 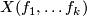 is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension
is a smooth, complex variety and in particular defines a closed, smooth, oriented dimensional manifold of real dimension  . This is called a complete intersection.
. This is called a complete intersection.
By a theorem of Thom [???] the diffeomorphism type of 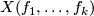 depends only upon the multi-degree,
depends only upon the multi-degree, 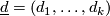 , and we write
, and we write 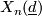 for
for 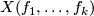 .
.
For example:
-
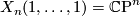 ,
,
-
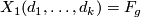 the oriented surface of genus
the oriented surface of genus 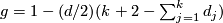 ,
,
-
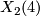 is a complex K3 surface,
is a complex K3 surface,
-
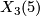 is a Calabi-Yau 3-fold.
is a Calabi-Yau 3-fold.
2 Invariants
By the Lefschetz hyperplane theorem the inclusion 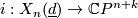 is an n-connected map. Hence:
is an n-connected map. Hence:
- if n > 1 then
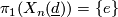 ,
,
-
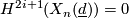 if
if 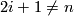 ,
,
-
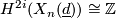 for all
for all 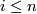 unless
unless 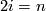 .
.
-
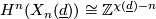 where
where 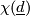 is the Euler characteristic of
is the Euler characteristic of 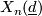 which we discuss further below.
which we discuss further below.
- When
 is even
is even 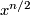 generates a summand of
generates a summand of 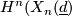 .
.
Note that here and throughout integer coefficients are use for (co)homology.
2.1 Cohomology ring
Let  be the canonical line bundle over
be the canonical line bundle over 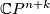 and let
and let 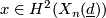 be defined by
be defined by 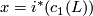 where
where 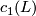 is the first Chern class of
is the first Chern class of  . Let
. Let
![[X_n({\underline{d}})] \in H_{2n}(X_n({\underline{d}}))](/images/math/f/4/2/f4299a7fd070d25d25a2a0cd434e0c6a.png) denote the fundamental class of
denote the fundamental class of 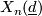 and let
and let 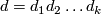 be the product of all degrees, called the total degree. We have the following useful identity [???]
be the product of all degrees, called the total degree. We have the following useful identity [???]
![\displaystyle \langle x^n, [X_n({\underline{d}})] \rangle = d.](/images/math/c/4/2/c42040a33bb3081f0d64c0ef9cba1e3b.png)
Let 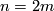 or
or 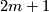 and consider the graded ring
and consider the graded ring
![\displaystyle H^*(n, d) :=\Zz[x, y]/\{x^{m+1} = dy, y^2 = 0 \}](/images/math/a/2/8/a2875558e0fa4f20ba7f73dbf2170c41.png)
where the dimensions of  and
and  are
are  and
and 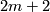 respectively. Let
respectively. Let 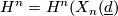 , considered as a graded ring in dimension
, considered as a graded ring in dimension 
- If
 is odd:
is odd:
- the ring
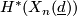 is determined by
is determined by  ,
,  and
and 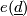 ,
,
- there is a short exact sequence
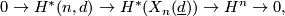
- the intersection form
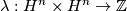 is of course skew hyperbolic.
is of course skew hyperbolic.
- the ring
- If
 is even:
is even:
- the ring
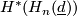 is determined by
is determined by  ,
,  and the pair
and the pair 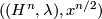 :
:
- there is a short exact sequence
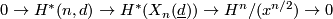 .
.
- Some properties of
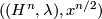 are described below.
are described below.
- the ring
Proposition 2.1 [Libgober&Wood1981].
If  is even, then
is even, then 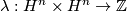 is indefinite unless
is indefinite unless 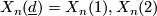 or
or 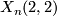 .
.
2.2 Characteristic classes
The stable tangent bundle of 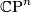 is isomorphic to
is isomorphic to 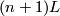 , [Milnor&Stasheff1974], and the normal bundle of the inclusion
, [Milnor&Stasheff1974], and the normal bundle of the inclusion 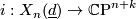 is given by the identity [???]
is given by the identity [???]
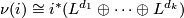
where 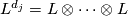 denotes the
denotes the 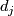 -fold tensor product of
-fold tensor product of  with itself. From this one deduces that the stable tangent bundle of
with itself. From this one deduces that the stable tangent bundle of 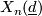 ,
, 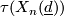 , satisfies the equation
, satisfies the equation
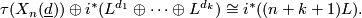
It follows immediately that the total Chern class and the total Pontrjagin class of 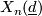 are given by
are given by
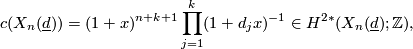
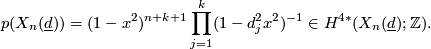
Moreover, the Euler class and Euler characteristic of 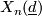 is given by
is given by
![\displaystyle e(X_n({\underline{d}})) = c_n(X_n({\underline{d}})), ~~~ \chi(\underline{d}) = \langle e(X_n(\underline{d}), [X_n(\underline{d})]\rangle.](/images/math/f/e/0/fe059d8703b858339f44a160448043ea.png)
3 Classification
The smooth classification of complete intersections for 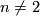 is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
is organised by the following conjecture, often called the Sullivan Conjecture after Dennis Sullivan.
Conjecture 3.1. For 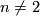 , complete intersections
, complete intersections 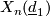 and
and 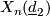 are diffeomorphic if and only if all of the following conditions hold
are diffeomorphic if and only if all of the following conditions hold
-
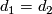 ,
,
-
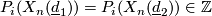 ,
,
-
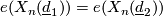 .
.
Note that we regard 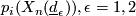 as multiplies of
as multiplies of 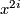 in order to view
in order to view 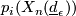 as an element of
as an element of  .
.
3.1 Classification in low dimensions
- For
 the Sullivan Conjecture holds by the classification of surfaces.
the Sullivan Conjecture holds by the classification of surfaces.
- For
 the topological Sullivan Conjecture holds for
the topological Sullivan Conjecture holds for  by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
by applying [Freedman1982]. The Sullivan Conjecture fails smoothly by [Ebeling1990] and [Libgober&Wood1990].
- For
 the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
the Sullivan Conjecture holds by [Wall1966] and [Jupp1973]. See the page 6-manifolds: 1-connected.
- For
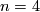 the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
the topological Sullivan Conjecture is true [Fang&Klaus1996]. Indeed, Fang and Klaus prove that the smooth conjecture, which is still open in general, holds up to connected sum with a homotopy 8-sphere.
- For
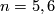 and
and  the topological Sullivan Conjecture is true [Fang&Wang2009].
the topological Sullivan Conjecture is true [Fang&Wang2009].
3.2 Further classification theorems
We now discuss further classification results for complete intersections. Let 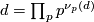 where
where  is prime.
is prime.
Theorem 3.2 [Traving1985].
If  and
and 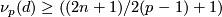 for all
for all  such that
such that 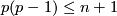 then the Sullivan Conjecture holds.
then the Sullivan Conjecture holds.
Traving's proof uses modified surgery: see [Kreck1999, Section 8] for a summary.
Theorem 3.3 [Fang1997].
If  and
and 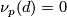 for all
for all  such that
such that 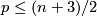 then the topological Sullivan Conjecture holds.
then the topological Sullivan Conjecture holds.
Fang's proof proceeds by extending results of [Libgober&Wood1982] on the homotopy classification of complete intersections where  is even to the case of
is even to the case of  odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
odd. He then solves the homeomorphism classification by exhibiting characteristic varieties for complete intersections and using them to calculate classical surgery obstructions. In particular he proves
Theorem 3.4 [Fang1997].
Let  and
and  be homotopy equivalent complete intersections. If
be homotopy equivalent complete intersections. If  is odd and
is odd and 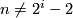 for all
for all 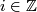 then
then  and
and  are homeomorphic to each other if and only if their Pontrjagin classes agree.
are homeomorphic to each other if and only if their Pontrjagin classes agree.
3.3 Classification up to homotopy
Recall that the signature of, 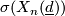 , of
, of 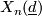 is the signature of its intersection form. If
is the signature of its intersection form. If  is odd
is odd 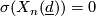 and if
and if  is even
is even 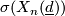 can be computed from the
can be computed from the 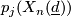 via Hirzebruch's signature theorem.
via Hirzebruch's signature theorem.
Theorem 3.5 [Libgober&Wood1982] and [Fang1997]. Let  and
and  be complete intersections with the same total degree
be complete intersections with the same total degree  . Suppose that
. Suppose that 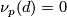 if
if 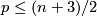 . If
. If 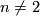 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteristic.
are homotopy equivalent if and only if they have the same signature and Euler characteristic.
Finally we summarise theorems of [Astey&Gitler&Micha&Pastor2003]. Define 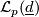 to be the unordered sequence
to be the unordered sequence

obtained by removing entries where 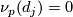 and write
and write  if
if 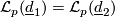 for all primes
for all primes  .
.
Theorem 3.6 [Astey&Gitler&Micha&Pastor2003].
If  and
and 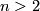 then
then  is homotopy equivalent to
is homotopy equivalent to  if and only if they have the same Euler characteristic and signature.
if and only if they have the same Euler characteristic and signature.
In contrast to the results of Fang and Ligober and Wood which hold when  is small relative to the primes dividing
is small relative to the primes dividing  , the above theorem leads to a homotopy classification which holds when
, the above theorem leads to a homotopy classification which holds when  is large relative to
is large relative to  . If
. If 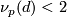 for all p then define
for all p then define 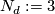 otherwise let
otherwise let
![\displaystyle N_d := \mathrm{Max} \{ 2(p_i-1)p_i^{[(\nu_{p}(d)-2)/2]} | \nu_{p}(d) \geq 2 \}.](/images/math/6/3/6/636ce5ebc2851f61f05adf3e72d0c8ec.png)
Theorem 3.7 [Astey&Gitler&Micha&Pastor2003].
If  and
and  have the same multidegree
have the same multidegree  and
and 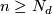 then
then  and
and  are homotopy equivalent if and only if they have the same signature and Euler characteritic.
are homotopy equivalent if and only if they have the same signature and Euler characteritic.
4 Further discussion
Conjecture 4.1 Hartshorne. Every smooth algebraic variety of dimension n which is embedded in 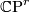 is isomorphic to a complete intersection, if
is isomorphic to a complete intersection, if 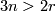 .
.
4.1 Splitting theorems
5 References
- [???] Template:???
- [Astey&Gitler&Micha&Pastor2003] L. Astey, S. Gitler, E. Micha and G. Pastor, On the homotopy type of complete intersections, Topology 44 (2005), no.1, 249–260. MR2104011 (2005i:14058) Zbl 1072.14063
- [Ebeling1990] W. Ebeling, An example of two homeomorphic, nondiffeomorphic complete intersection surfaces, Invent. Math. 99 (1990), no.3, 651–654. MR1032884 (91c:57038) Zbl 0707.14045
- [Fang&Klaus1996] F. Fang and S. Klaus, Topological classification of
 -dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
-dimensional complete intersections, Manuscripta Math. 90 (1996), no.2, 139–147. MR1391206 (97g:57046) Zbl 0866.57015
- [Fang&Wang2009] F. Fang and J. Wang, Homeomorphism classification of complex projective complete intersections of dimensions 5, 6 and 7, to appear in Math. Zeit. (2009).
- [Fang1997] F. Fang, Topology of complete intersections, Comment. Math. Helv. 72 (1997), no.3, 466–480. MR1476060 (98k:14071) Zbl 0896.14028
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Libgober&Wood1981] A. S. Libgober and J. W. Wood, On the topological structure of even-dimensional complete intersections, Trans. Amer. Math. Soc. 267 (1981), no.2, 637–660. MR626495 (83e:57017) Zbl 0475.57013
- [Libgober&Wood1982] A. S. Libgober and J. W. Wood, Differentiable structures on complete intersections. I, Topology 21 (1982), no.4, 469–482. MR670748 (84a:57037) Zbl 0504.57015
- [Libgober&Wood1990] A. S. Libgober and J. W. Wood, Uniqueness of the complex structure on Kähler manifolds of certain homotopy types, J. Differential Geom. 32 (1990), no.1, 139–154. MR1064869 (91g:32039) Zbl 0711.53052
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Traving1985] C. Traving, Zur Diffeomorphieklassifikation vollständiger Durchschnitte, Diplomarbeit, Mainz (1985).
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
6 External links
- The Wikipedia page about complete intersections