Characteristic rank of a real vector bundle
|
The user responsible for this page is Ludovit Balko . No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Definition
 be a connected, finite
be a connected, finite 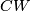 -complex and
-complex and  a real vector bundle over
a real vector bundle over  . The characteristic rank of the vector bundle
. The characteristic rank of the vector bundle  over
over  , denoted by
, denoted by 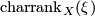 , is the largest integer
, is the largest integer  ,
, 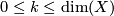 , such that every cohomology class
, such that every cohomology class 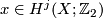 ,
, 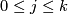 , is a polynomial in the Stiefel-Whitney classes
, is a polynomial in the Stiefel-Whitney classes 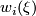 of
of  . If
. If  is closed, smooth, connected manifold, characteristic rank of manifold
is closed, smooth, connected manifold, characteristic rank of manifold  , denoted by
, denoted by 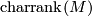 is defined as characteristic rank of
is defined as characteristic rank of 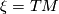 , the tangent bundle of
, the tangent bundle of  .
.Bundle dependency then admits the following definition of the upper characteristic rank of 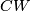 -complex
-complex  .
.
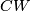 -complex
-complex  ,
,  is maximum of
is maximum of 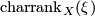 as
as  varies over all vector bundles over
varies over all vector bundles over  .
.2 Motivation
For closed, smooth, connected  -dimensional manifold
-dimensional manifold  unorientedly cobordant to zero, there exist an element in
unorientedly cobordant to zero, there exist an element in 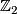 -cohomology algebra
-cohomology algebra 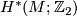 of
of  , which cannot be expressed as a polynomial in Stiefel-Whitney classes
, which cannot be expressed as a polynomial in Stiefel-Whitney classes 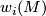 of (tangent bundle of) manifold
of (tangent bundle of) manifold  . For this type of manifold there is the following estimate of
. For this type of manifold there is the following estimate of 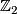 cuplength of manifold
cuplength of manifold  .
.
Theorem 2.1.[Korbaš2010] Let  be a closed smooth connected
be a closed smooth connected  -dimensional manifold unorientedly cobordant to zero. Let
-dimensional manifold unorientedly cobordant to zero. Let 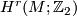 ,
, 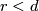 , be the first nonzero reduced cohomology group of
, be the first nonzero reduced cohomology group of  . Let
. Let 
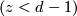 be an integer such that for
be an integer such that for 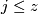 each element of
each element of 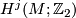 can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold
can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold  . Then we have that
. Then we have that
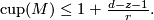
This leads the definition of characteristic rank of manifold  , which is the largest possible
, which is the largest possible  which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold
which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold  with connected, finite
with connected, finite 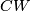 -complex and tangent bundle
-complex and tangent bundle  of
of  with a real vector bundle
with a real vector bundle  , gives definition 1.1 [Naolekar&Thakur2014].
, gives definition 1.1 [Naolekar&Thakur2014].
3 Examples
The  cohomology ring of
cohomology ring of  -dimensional real projective space is
-dimensional real projective space is ![H^\ast(\mathbb{R}P^n;\mathbb{Z}_2)=\mathbb{Z}_2[w_1(\gamma_n^1)]/(w_1(\gamma_n^1)^{n+1})](/images/math/5/8/d/58d5c0e0093743b2591997247a518a3c.png) , where
, where 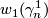 is the first Stiefel-Whitney characteristic class of canonical line bundle
is the first Stiefel-Whitney characteristic class of canonical line bundle 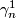 over
over 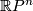 [Milnor&Stasheff1974]. It is then clear, that
[Milnor&Stasheff1974]. It is then clear, that 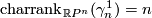 .
On the other hand, we have
.
On the other hand, we have 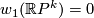 for
for  odd and
odd and 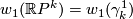 for k even. In this case
for k even. In this case 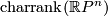 equals
equals  if
if  is odd, and equals
is odd, and equals  if
if  is even.
is even.
4 References
- [Korbaš2010] J. Korbaš, The cup-length of the oriented Grassmannians vs a new bound for zero-cobordant manifolds, Bull. Belg. Math. Soc. Simon Stevin 17 (2010), 69–81.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Naolekar&Thakur2014] A. C. Naolekar and A. S. Thakur, Note on the characteristic rank of vector bundles, Math. Slovaca (2014) 64: 1525. https://doi.org/10.2478/s12175-014-0289-4
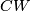 -complex and
-complex and  a real vector bundle over
a real vector bundle over  . The characteristic rank of the vector bundle
. The characteristic rank of the vector bundle  over
over  , denoted by
, denoted by 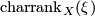 , is the largest integer
, is the largest integer  ,
, 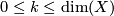 , such that every cohomology class
, such that every cohomology class 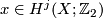 ,
, 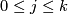 , is a polynomial in the Stiefel-Whitney classes
, is a polynomial in the Stiefel-Whitney classes 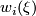 of
of  . If
. If  is closed, smooth, connected manifold, characteristic rank of manifold
is closed, smooth, connected manifold, characteristic rank of manifold  , denoted by
, denoted by 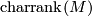 is defined as characteristic rank of
is defined as characteristic rank of 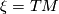 , the tangent bundle of
, the tangent bundle of  .
.Bundle dependency then admits the following definition of the upper characteristic rank of 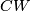 -complex
-complex  .
.
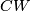 -complex
-complex  ,
,  is maximum of
is maximum of 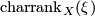 as
as  varies over all vector bundles over
varies over all vector bundles over  .
.2 Motivation
For closed, smooth, connected  -dimensional manifold
-dimensional manifold  unorientedly cobordant to zero, there exist an element in
unorientedly cobordant to zero, there exist an element in 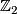 -cohomology algebra
-cohomology algebra 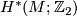 of
of  , which cannot be expressed as a polynomial in Stiefel-Whitney classes
, which cannot be expressed as a polynomial in Stiefel-Whitney classes 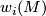 of (tangent bundle of) manifold
of (tangent bundle of) manifold  . For this type of manifold there is the following estimate of
. For this type of manifold there is the following estimate of 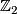 cuplength of manifold
cuplength of manifold  .
.
Theorem 2.1.[Korbaš2010] Let  be a closed smooth connected
be a closed smooth connected  -dimensional manifold unorientedly cobordant to zero. Let
-dimensional manifold unorientedly cobordant to zero. Let 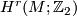 ,
, 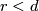 , be the first nonzero reduced cohomology group of
, be the first nonzero reduced cohomology group of  . Let
. Let 
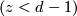 be an integer such that for
be an integer such that for 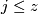 each element of
each element of 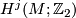 can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold
can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold  . Then we have that
. Then we have that
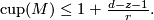
This leads the definition of characteristic rank of manifold  , which is the largest possible
, which is the largest possible  which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold
which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold  with connected, finite
with connected, finite  -complex and tangent bundle
-complex and tangent bundle  of
of  with a real vector bundle
with a real vector bundle  , gives definition 1.1 [Naolekar&Thakur2014].
, gives definition 1.1 [Naolekar&Thakur2014].
3 Examples
The 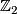 cohomology ring of
cohomology ring of  -dimensional real projective space is
-dimensional real projective space is ![H^\ast(\mathbb{R}P^n;\mathbb{Z}_2)=\mathbb{Z}_2[w_1(\gamma_n^1)]/(w_1(\gamma_n^1)^{n+1})](/images/math/5/8/d/58d5c0e0093743b2591997247a518a3c.png) , where
, where 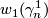 is the first Stiefel-Whitney characteristic class of canonical line bundle
is the first Stiefel-Whitney characteristic class of canonical line bundle 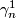 over
over 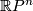 [Milnor&Stasheff1974]. It is then clear, that
[Milnor&Stasheff1974]. It is then clear, that 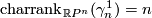 .
On the other hand, we have
.
On the other hand, we have 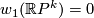 for
for  odd and
odd and 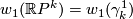 for k even. In this case
for k even. In this case 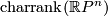 equals
equals  if
if  is odd, and equals
is odd, and equals  if
if  is even.
is even.
4 References
- [Korbaš2010] J. Korbaš, The cup-length of the oriented Grassmannians vs a new bound for zero-cobordant manifolds, Bull. Belg. Math. Soc. Simon Stevin 17 (2010), 69–81.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Naolekar&Thakur2014] A. C. Naolekar and A. S. Thakur, Note on the characteristic rank of vector bundles, Math. Slovaca (2014) 64: 1525. https://doi.org/10.2478/s12175-014-0289-4
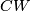 -complex and
-complex and  a real vector bundle over
a real vector bundle over  . The characteristic rank of the vector bundle
. The characteristic rank of the vector bundle  over
over  , denoted by
, denoted by 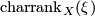 , is the largest integer
, is the largest integer  ,
, 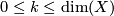 , such that every cohomology class
, such that every cohomology class 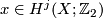 ,
, 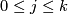 , is a polynomial in the Stiefel-Whitney classes
, is a polynomial in the Stiefel-Whitney classes 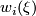 of
of  . If
. If  is closed, smooth, connected manifold, characteristic rank of manifold
is closed, smooth, connected manifold, characteristic rank of manifold  , denoted by
, denoted by 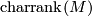 is defined as characteristic rank of
is defined as characteristic rank of 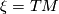 , the tangent bundle of
, the tangent bundle of  .
.Bundle dependency then admits the following definition of the upper characteristic rank of 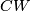 -complex
-complex  .
.
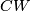 -complex
-complex  ,
,  is maximum of
is maximum of 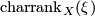 as
as  varies over all vector bundles over
varies over all vector bundles over  .
.2 Motivation
For closed, smooth, connected  -dimensional manifold
-dimensional manifold  unorientedly cobordant to zero, there exist an element in
unorientedly cobordant to zero, there exist an element in 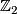 -cohomology algebra
-cohomology algebra 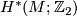 of
of  , which cannot be expressed as a polynomial in Stiefel-Whitney classes
, which cannot be expressed as a polynomial in Stiefel-Whitney classes 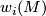 of (tangent bundle of) manifold
of (tangent bundle of) manifold  . For this type of manifold there is the following estimate of
. For this type of manifold there is the following estimate of 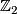 cuplength of manifold
cuplength of manifold  .
.
Theorem 2.1.[Korbaš2010] Let  be a closed smooth connected
be a closed smooth connected  -dimensional manifold unorientedly cobordant to zero. Let
-dimensional manifold unorientedly cobordant to zero. Let 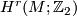 ,
, 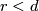 , be the first nonzero reduced cohomology group of
, be the first nonzero reduced cohomology group of  . Let
. Let 
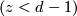 be an integer such that for
be an integer such that for 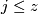 each element of
each element of 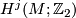 can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold
can be expressed as a polynomial in the Stiefel-Whitney classes of the manifold  . Then we have that
. Then we have that
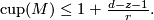
This leads the definition of characteristic rank of manifold  , which is the largest possible
, which is the largest possible  which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold
which fulfills the conditions of the theorem above.
Making the definition of characteristic rank bundle dependent, i.e. replacing manifold  with connected, finite
with connected, finite  -complex and tangent bundle
-complex and tangent bundle  of
of  with a real vector bundle
with a real vector bundle  , gives definition 1.1 [Naolekar&Thakur2014].
, gives definition 1.1 [Naolekar&Thakur2014].
3 Examples
The  cohomology ring of
cohomology ring of  -dimensional real projective space is
-dimensional real projective space is ![H^\ast(\mathbb{R}P^n;\mathbb{Z}_2)=\mathbb{Z}_2[w_1(\gamma_n^1)]/(w_1(\gamma_n^1)^{n+1})](/images/math/5/8/d/58d5c0e0093743b2591997247a518a3c.png) , where
, where 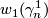 is the first Stiefel-Whitney characteristic class of canonical line bundle
is the first Stiefel-Whitney characteristic class of canonical line bundle 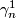 over
over 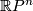 [Milnor&Stasheff1974]. It is then clear, that
[Milnor&Stasheff1974]. It is then clear, that 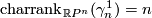 .
On the other hand, we have
.
On the other hand, we have 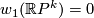 for
for  odd and
odd and 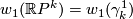 for k even. In this case
for k even. In this case 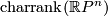 equals
equals  if
if  is odd, and equals
is odd, and equals  if
if  is even.
is even.
4 References
- [Korbaš2010] J. Korbaš, The cup-length of the oriented Grassmannians vs a new bound for zero-cobordant manifolds, Bull. Belg. Math. Soc. Simon Stevin 17 (2010), 69–81.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Naolekar&Thakur2014] A. C. Naolekar and A. S. Thakur, Note on the characteristic rank of vector bundles, Math. Slovaca (2014) 64: 1525. https://doi.org/10.2478/s12175-014-0289-4
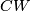 -complex and
-complex and  a real vector bundle over
a real vector bundle over  . The characteristic rank of the vector bundle
. The characteristic rank of the vector bundle  over
over  , denoted by
, denoted by 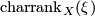 , is the largest integer
, is the largest integer  ,
, 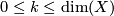 , such that every cohomology class
, such that every cohomology class 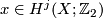 ,
, 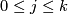 , is a polynomial in the Stiefel-Whitney classes
, is a polynomial in the Stiefel-Whitney classes 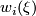 of
of  . If
. If  is closed, smooth, connected manifold, characteristic rank of manifold
is closed, smooth, connected manifold, characteristic rank of manifold  , denoted by
, denoted by 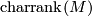 is defined as characteristic rank of
is defined as characteristic rank of 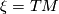 , the tangent bundle of
, the tangent bundle of  .
.