Chain duality V (Ex)
From Manifold Atlas
(Difference between revisions)
| Line 13: | Line 13: | ||
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| − | [[Category:Exercises | + | [[Category:Exercises with solution]] |
Latest revision as of 18:08, 31 May 2012
Let 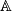 be an additive category with chain duality
be an additive category with chain duality 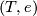 . Show that under the isomorphism
. Show that under the isomorphism
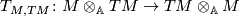
we have
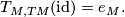
Observe that  can be defined this way if we have already defined
can be defined this way if we have already defined  and
and 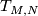 .
.