Chain duality III (Ex)
From Manifold Atlas
Revision as of 17:59, 1 June 2012 by Martin Olbermann (Talk | contribs)
Let 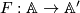 be a functor of additive categories with chain duality. Show that the assignment
be a functor of additive categories with chain duality. Show that the assignment
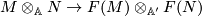
given by
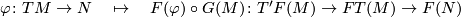
induces a  -equivariant chain map
-equivariant chain map
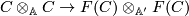
for any 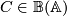 .
.