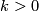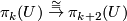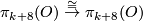Bott periodicity and exotic spheres: some comments
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 The Bott periodicity Theorem
One of the fundamental results in modern topology is Bott periodicity [Bott]. It concerns the homotopy groups of the stable orthogonal or unitary groups 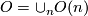 resp
resp 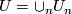 :
:
 : For
: For 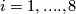 one has
one has 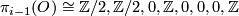
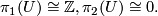
2 An interpretation in terms of vector bundles over spheres
Most applications of this result concern the interpretation of these groups as stable vector bundles over spheres. Namely if 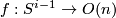 is a continuous map, then one obtains a vector bundle
is a continuous map, then one obtains a vector bundle 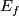 over
over 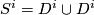 by taking two copies of
by taking two copies of 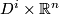 and by identifying
and by identifying 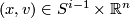 in the first copy with
in the first copy with 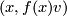 in the second copy. This map gives an isomorphism from
in the second copy. This map gives an isomorphism from 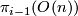 to the set
to the set 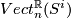 of isomorphism classes of
of isomorphism classes of  -dimensional vector bundles over
-dimensional vector bundles over  . I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly
. I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly 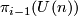 corresponds to the set
corresponds to the set 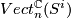 of isomorphism classes of complex
of isomorphism classes of complex  -dimensional vector bundles over
-dimensional vector bundles over  . Passing from
. Passing from  to
to 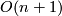 (or
(or 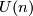 to
to 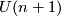 ) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the
) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the  -dimensional trivial bundle. By a general position argument the stabilization map is a bijection if
-dimensional trivial bundle. By a general position argument the stabilization map is a bijection if 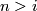 (
(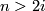 in the complex case). If
in the complex case). If 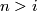 (or
(or 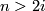 in the complex case) one calls such a bundle a stable vector bundle. Actually the
in the complex case) one calls such a bundle a stable vector bundle. Actually the  -dimensional vector bundles over
-dimensional vector bundles over  (not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for
(not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for 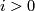 not equal to
not equal to 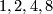 mod
mod  all real vector bundles of dimension
all real vector bundles of dimension 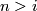 over
over  are trivial, that for
are trivial, that for 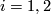 mod
mod  there are precisely
there are precisely  such bundles and for
such bundles and for 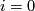 mod
mod  there are countably many such bundles.
there are countably many such bundles.
Remark 2.1. I find it remarkable that Bott doesn't mention the relation to vector bundles. Actually Bott does not say a single word, why his result is interesting. He obviously assumes that a reader finds the problem to determine the homotopy groups of such fundamental objects like the stable orthogonal or unitary group interesting in itself and he is of course right. Whether he has foreseen that it is such a fundamental result would be interesting to know, perhaps his friends Atiyah and Hirzebruch can comment on this.
3 The dates and dates of background papers
The paper with complete proofs appeared in September 1959, it was submitted November 1958. An announcement containing the above statements appeared in 1957 [Bott1957]. The methods of the proof were developed in several earlier papers [Bott1954], [Bott 1956].
4 The role of Bott periodicity for Kervaire-Milnor's paper
I hope there will be many articles in the atlas explaining more or less immediate applications of the periodicity theorem. Here I comment on the role it played in Kervaire and Milnor's important paper "Groups of homotopy spheres I" [Kervaire&Milnor1963]. This paper appeared May 1963, and was submitted April 1962. By that time the periodicity theorem must have been a standard tool in topology.
A smooth manifold homotopy equivalent to a sphere is called a homotopy sphere. Such manifolds are interesting for many reasons, one of them is the Poincaré conjecture saying that all these manifolds are homeomorphic to the standard sphere. There are no obvious constructions of such manifolds. But Milnor [Milnor1956] constructed a series of  -dimensional manifolds which are all homeomorphic to the
-dimensional manifolds which are all homeomorphic to the  -sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
-sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
The Poincaré conjecture was proven by Smale, Stallings and Zeeman (references) for 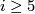 already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension
already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension  and by Perelmann [Perelman] in dimension
and by Perelmann [Perelman] in dimension  . Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
. Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
If  is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
Theorem [Kervaire-Milnor1963] 4.1. For all homotopy spheres  the stable tangent bundle is trivial.
the stable tangent bundle is trivial.
The proof of this theorem is based on three non-trivial theorems, one of which is Bott periodicity. This makes it in half of the cases a triviality, since for 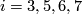 mod
mod  there is no non-trivial stable vector bundle over
there is no non-trivial stable vector bundle over  . The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over
. The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over  are isomorphic. Let's begin with the case
are isomorphic. Let's begin with the case 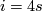 .
.
In the case 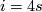 one has an invariant for stable vector bundles
one has an invariant for stable vector bundles  , namely the Pontrjagin classes
, namely the Pontrjagin classes 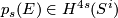 . It turns out that this map is a homomorphism from the stable vector bundles over
. It turns out that this map is a homomorphism from the stable vector bundles over 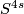 to
to 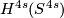 which by choosing an orientation we identify with
which by choosing an orientation we identify with  . Thus we have a homomorphism from a group isomorphic to
. Thus we have a homomorphism from a group isomorphic to  to
to  , and if it is non-trivial it is an injection implying that two stable vector bundles over
, and if it is non-trivial it is an injection implying that two stable vector bundles over 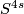 are isomorphic if and only their Pontrjagin classes
are isomorphic if and only their Pontrjagin classes 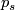 agree. To show that the homomorphism is non-trivial (for
agree. To show that the homomorphism is non-trivial (for  ) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
Kervaire and Milnor proceed slightly differently. They refer to obstruction theory, a theory which can be used to decide whether a vector bundle is trivial. They say (with reference to earlier papers by Kervaire) that the obstruction class and the Pontrjagin class 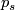 are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a
are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a 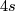 -dimensional homotopy sphere
-dimensional homotopy sphere  is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class
is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class 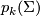 is a multiple of the signature
is a multiple of the signature 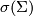 , which is zero since
, which is zero since 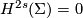 ."
."
Remark 4.2. Let me make a short comment on this sentence. It shows that the signature theorem, which was published by Hirzebruch in his 1956 book, is at the time when Kervaire and Milnor wrote their paper so standard, that neither a reference to Hirzebruch's book is needed (which appears in the list of references but no reference is given at this place) nor the formula of the signature theorem is repeated.
A non-trivial theorem is also needed in the remaining cases where 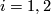 mod
mod  is. The cases
is. The cases  and
and  are trivial, but the higher dimensions not. Here the obstruction class sits in
are trivial, but the higher dimensions not. Here the obstruction class sits in 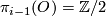 (by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form
(by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form  . There is a homomorphism introduced by Hopf-Whitehead (reference), the
. There is a homomorphism introduced by Hopf-Whitehead (reference), the 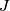 -homomorphism, from
-homomorphism, from 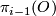 to the stable homotopy groups
to the stable homotopy groups 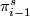 of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this
of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this 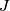 -homomorphism is injective.
-homomorphism is injective.
5 Some comments
After repeating the role of Bott periodicity in the proof of this theorem I would like to comment a bit on the role of this theorem in the paper of Kervaire and Milnor and in the further development of analyzing smooth structures on a topological manifold, here the sphere.
On the one hand the message of the theorem is negative, one cannot use the stable tangent bundle to distinguish different smooth structures on the sphere. This leads to the interesting question, whether the same is true for arbitrary manifolds. Later in the sixties some very deep theorems in this direction were proved.
On the other hand the theorem was a good start to develop a method to study the different smooth structures on spheres or equivalently the homotopy spheres in dimension 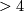 , a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds
, a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds  and
and  of dimension
of dimension 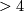 are diffeomorphic is to try to find an
are diffeomorphic is to try to find an  -cobordism between them, that is a compact manifold
-cobordism between them, that is a compact manifold  with boundary the disjoint union of
with boundary the disjoint union of  and
and  , such that the inclusions from
, such that the inclusions from  and
and  to
to  are homotopy equivalent (up to homotopy
are homotopy equivalent (up to homotopy  is cylinder). Then Smale's
is cylinder). Then Smale's  -cobordism theorem [Smale1961] implies that if the dimension of
-cobordism theorem [Smale1961] implies that if the dimension of  is larger than
is larger than  , then
, then  is diffeomorphic to the cylinder
is diffeomorphic to the cylinder ![M \times [0,1]](/images/math/b/2/e/b2eae1bd719f40c8fec914d995272cc8.png) , and so
, and so  and
and  are diffeomorphic.
are diffeomorphic.
Thus one tries to find an  -cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for
-cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for  . Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an
. Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an  -cobordism. They solve this problem completely by surgery theory.
-cobordism. They solve this problem completely by surgery theory.
Remark 5.1.
Suppose that a topological manifold  is given. Then one can ask whether
is given. Then one can ask whether  admits a smooth structure. A necessary condition is that
admits a smooth structure. A necessary condition is that  has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension
has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension 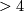 , but false in dimension
, but false in dimension  by the fundamental work of Donaldson (reference), and again true in dimension
by the fundamental work of Donaldson (reference), and again true in dimension 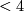 by different methods (Kirby-Sibenmann (reference)).
by different methods (Kirby-Sibenmann (reference)).
If we assume that  has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension
has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension 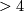 ). Roughly speaking the different smooth structures on
). Roughly speaking the different smooth structures on  correspond to the different ways to impose a stable tangent bundle on
correspond to the different ways to impose a stable tangent bundle on  (Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called
(Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called  -theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
-theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
6 References
- [Adams] Template:Adams
- [Atiyah-Hirzebruch] Template:Atiyah-Hirzebruch
- [Bott] Template:Bott
- [Bott 1956] Template:Bott 1956
- [Bott1954] Template:Bott1954
- [Bott1957] R. Bott, The stable homotopy of the classical groups, Proc. Nat. Acad. Sci. U.S.A. 43 (1957), 933–935. MR0102802 (21 #1588) Zbl 0129.15601
- [Bott1958] Template:Bott1958
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1958] Template:Kervaire&Milnor1958
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire-Milnor1963] Template:Kervaire-Milnor1963
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Perelman] Template:Perelman
- [Smale1961] S. Smale, Generalized Poincaré's conjecture in dimensions greater than four, Ann. of Math. (2) 74 (1961), 391–406. MR0137124 (25 #580) Zbl 0099.39202
- [Steenrod] Template:Steenrod
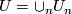 :
Thus one only needs to know the groups for small
:
Thus one only needs to know the groups for small  : For
: For 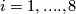 one has
one has 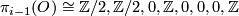
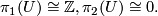
2 An interpretation in terms of vector bundles over spheres
Most applications of this result concern the interpretation of these groups as stable vector bundles over spheres. Namely if 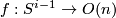 is a continuous map, then one obtains a vector bundle
is a continuous map, then one obtains a vector bundle 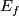 over
over 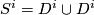 by taking two copies of
by taking two copies of 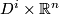 and by identifying
and by identifying 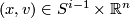 in the first copy with
in the first copy with 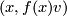 in the second copy. This map gives an isomorphism from
in the second copy. This map gives an isomorphism from 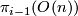 to the set
to the set 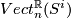 of isomorphism classes of
of isomorphism classes of  -dimensional vector bundles over
-dimensional vector bundles over  . I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly
. I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly 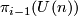 corresponds to the set
corresponds to the set 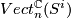 of isomorphism classes of complex
of isomorphism classes of complex  -dimensional vector bundles over
-dimensional vector bundles over  . Passing from
. Passing from  to
to 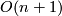 (or
(or 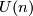 to
to 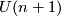 ) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the
) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the  -dimensional trivial bundle. By a general position argument the stabilization map is a bijection if
-dimensional trivial bundle. By a general position argument the stabilization map is a bijection if 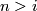 (
(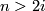 in the complex case). If
in the complex case). If 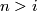 (or
(or 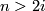 in the complex case) one calls such a bundle a stable vector bundle. Actually the
in the complex case) one calls such a bundle a stable vector bundle. Actually the  -dimensional vector bundles over
-dimensional vector bundles over  (not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for
(not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for 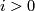 not equal to
not equal to 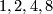 mod
mod  all real vector bundles of dimension
all real vector bundles of dimension 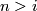 over
over  are trivial, that for
are trivial, that for 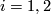 mod
mod  there are precisely
there are precisely  such bundles and for
such bundles and for 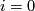 mod
mod  there are countably many such bundles.
there are countably many such bundles.
Remark 2.1. I find it remarkable that Bott doesn't mention the relation to vector bundles. Actually Bott does not say a single word, why his result is interesting. He obviously assumes that a reader finds the problem to determine the homotopy groups of such fundamental objects like the stable orthogonal or unitary group interesting in itself and he is of course right. Whether he has foreseen that it is such a fundamental result would be interesting to know, perhaps his friends Atiyah and Hirzebruch can comment on this.
3 The dates and dates of background papers
The paper with complete proofs appeared in September 1959, it was submitted November 1958. An announcement containing the above statements appeared in 1957 [Bott1957]. The methods of the proof were developed in several earlier papers [Bott1954], [Bott 1956].
4 The role of Bott periodicity for Kervaire-Milnor's paper
I hope there will be many articles in the atlas explaining more or less immediate applications of the periodicity theorem. Here I comment on the role it played in Kervaire and Milnor's important paper "Groups of homotopy spheres I" [Kervaire&Milnor1963]. This paper appeared May 1963, and was submitted April 1962. By that time the periodicity theorem must have been a standard tool in topology.
A smooth manifold homotopy equivalent to a sphere is called a homotopy sphere. Such manifolds are interesting for many reasons, one of them is the Poincaré conjecture saying that all these manifolds are homeomorphic to the standard sphere. There are no obvious constructions of such manifolds. But Milnor [Milnor1956] constructed a series of  -dimensional manifolds which are all homeomorphic to the
-dimensional manifolds which are all homeomorphic to the  -sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
-sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
The Poincaré conjecture was proven by Smale, Stallings and Zeeman (references) for 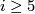 already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension
already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension  and by Perelmann [Perelman] in dimension
and by Perelmann [Perelman] in dimension  . Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
. Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
If  is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
Theorem [Kervaire-Milnor1963] 4.1. For all homotopy spheres  the stable tangent bundle is trivial.
the stable tangent bundle is trivial.
The proof of this theorem is based on three non-trivial theorems, one of which is Bott periodicity. This makes it in half of the cases a triviality, since for 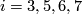 mod
mod  there is no non-trivial stable vector bundle over
there is no non-trivial stable vector bundle over  . The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over
. The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over  are isomorphic. Let's begin with the case
are isomorphic. Let's begin with the case 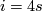 .
.
In the case 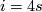 one has an invariant for stable vector bundles
one has an invariant for stable vector bundles  , namely the Pontrjagin classes
, namely the Pontrjagin classes 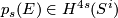 . It turns out that this map is a homomorphism from the stable vector bundles over
. It turns out that this map is a homomorphism from the stable vector bundles over 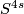 to
to 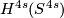 which by choosing an orientation we identify with
which by choosing an orientation we identify with  . Thus we have a homomorphism from a group isomorphic to
. Thus we have a homomorphism from a group isomorphic to  to
to  , and if it is non-trivial it is an injection implying that two stable vector bundles over
, and if it is non-trivial it is an injection implying that two stable vector bundles over 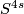 are isomorphic if and only their Pontrjagin classes
are isomorphic if and only their Pontrjagin classes 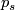 agree. To show that the homomorphism is non-trivial (for
agree. To show that the homomorphism is non-trivial (for  ) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
Kervaire and Milnor proceed slightly differently. They refer to obstruction theory, a theory which can be used to decide whether a vector bundle is trivial. They say (with reference to earlier papers by Kervaire) that the obstruction class and the Pontrjagin class 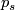 are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a
are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a 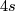 -dimensional homotopy sphere
-dimensional homotopy sphere  is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class
is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class 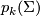 is a multiple of the signature
is a multiple of the signature 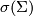 , which is zero since
, which is zero since 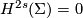 ."
."
Remark 4.2. Let me make a short comment on this sentence. It shows that the signature theorem, which was published by Hirzebruch in his 1956 book, is at the time when Kervaire and Milnor wrote their paper so standard, that neither a reference to Hirzebruch's book is needed (which appears in the list of references but no reference is given at this place) nor the formula of the signature theorem is repeated.
A non-trivial theorem is also needed in the remaining cases where 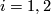 mod
mod  is. The cases
is. The cases  and
and  are trivial, but the higher dimensions not. Here the obstruction class sits in
are trivial, but the higher dimensions not. Here the obstruction class sits in 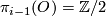 (by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form
(by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form  . There is a homomorphism introduced by Hopf-Whitehead (reference), the
. There is a homomorphism introduced by Hopf-Whitehead (reference), the 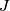 -homomorphism, from
-homomorphism, from 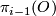 to the stable homotopy groups
to the stable homotopy groups 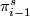 of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this
of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this 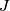 -homomorphism is injective.
-homomorphism is injective.
5 Some comments
After repeating the role of Bott periodicity in the proof of this theorem I would like to comment a bit on the role of this theorem in the paper of Kervaire and Milnor and in the further development of analyzing smooth structures on a topological manifold, here the sphere.
On the one hand the message of the theorem is negative, one cannot use the stable tangent bundle to distinguish different smooth structures on the sphere. This leads to the interesting question, whether the same is true for arbitrary manifolds. Later in the sixties some very deep theorems in this direction were proved.
On the other hand the theorem was a good start to develop a method to study the different smooth structures on spheres or equivalently the homotopy spheres in dimension 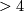 , a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds
, a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds  and
and  of dimension
of dimension 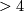 are diffeomorphic is to try to find an
are diffeomorphic is to try to find an  -cobordism between them, that is a compact manifold
-cobordism between them, that is a compact manifold  with boundary the disjoint union of
with boundary the disjoint union of  and
and  , such that the inclusions from
, such that the inclusions from  and
and  to
to  are homotopy equivalent (up to homotopy
are homotopy equivalent (up to homotopy  is cylinder). Then Smale's
is cylinder). Then Smale's  -cobordism theorem [Smale1961] implies that if the dimension of
-cobordism theorem [Smale1961] implies that if the dimension of  is larger than
is larger than  , then
, then  is diffeomorphic to the cylinder
is diffeomorphic to the cylinder ![M \times [0,1]](/images/math/b/2/e/b2eae1bd719f40c8fec914d995272cc8.png) , and so
, and so  and
and  are diffeomorphic.
are diffeomorphic.
Thus one tries to find an  -cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for
-cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for  . Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an
. Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an  -cobordism. They solve this problem completely by surgery theory.
-cobordism. They solve this problem completely by surgery theory.
Remark 5.1.
Suppose that a topological manifold  is given. Then one can ask whether
is given. Then one can ask whether  admits a smooth structure. A necessary condition is that
admits a smooth structure. A necessary condition is that  has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension
has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension 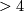 , but false in dimension
, but false in dimension  by the fundamental work of Donaldson (reference), and again true in dimension
by the fundamental work of Donaldson (reference), and again true in dimension 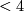 by different methods (Kirby-Sibenmann (reference)).
by different methods (Kirby-Sibenmann (reference)).
If we assume that  has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension
has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension 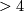 ). Roughly speaking the different smooth structures on
). Roughly speaking the different smooth structures on  correspond to the different ways to impose a stable tangent bundle on
correspond to the different ways to impose a stable tangent bundle on  (Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called
(Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called  -theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
-theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
6 References
- [Adams] Template:Adams
- [Atiyah-Hirzebruch] Template:Atiyah-Hirzebruch
- [Bott] Template:Bott
- [Bott 1956] Template:Bott 1956
- [Bott1954] Template:Bott1954
- [Bott1957] R. Bott, The stable homotopy of the classical groups, Proc. Nat. Acad. Sci. U.S.A. 43 (1957), 933–935. MR0102802 (21 #1588) Zbl 0129.15601
- [Bott1958] Template:Bott1958
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1958] Template:Kervaire&Milnor1958
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire-Milnor1963] Template:Kervaire-Milnor1963
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Perelman] Template:Perelman
- [Smale1961] S. Smale, Generalized Poincaré's conjecture in dimensions greater than four, Ann. of Math. (2) 74 (1961), 391–406. MR0137124 (25 #580) Zbl 0099.39202
- [Steenrod] Template:Steenrod
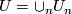 :
Thus one only needs to know the groups for small
:
Thus one only needs to know the groups for small  : For
: For 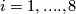 one has
one has 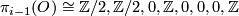
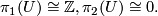
2 An interpretation in terms of vector bundles over spheres
Most applications of this result concern the interpretation of these groups as stable vector bundles over spheres. Namely if 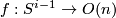 is a continuous map, then one obtains a vector bundle
is a continuous map, then one obtains a vector bundle 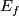 over
over 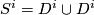 by taking two copies of
by taking two copies of 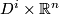 and by identifying
and by identifying 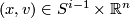 in the first copy with
in the first copy with 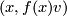 in the second copy. This map gives an isomorphism from
in the second copy. This map gives an isomorphism from 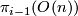 to the set
to the set 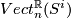 of isomorphism classes of
of isomorphism classes of  -dimensional vector bundles over
-dimensional vector bundles over  . I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly
. I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly 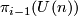 corresponds to the set
corresponds to the set 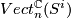 of isomorphism classes of complex
of isomorphism classes of complex  -dimensional vector bundles over
-dimensional vector bundles over  . Passing from
. Passing from  to
to 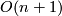 (or
(or 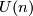 to
to 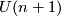 ) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the
) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the  -dimensional trivial bundle. By a general position argument the stabilization map is a bijection if
-dimensional trivial bundle. By a general position argument the stabilization map is a bijection if 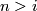 (
(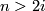 in the complex case). If
in the complex case). If 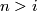 (or
(or 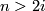 in the complex case) one calls such a bundle a stable vector bundle. Actually the
in the complex case) one calls such a bundle a stable vector bundle. Actually the  -dimensional vector bundles over
-dimensional vector bundles over  (not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for
(not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for 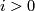 not equal to
not equal to 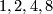 mod
mod  all real vector bundles of dimension
all real vector bundles of dimension 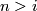 over
over  are trivial, that for
are trivial, that for 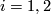 mod
mod  there are precisely
there are precisely  such bundles and for
such bundles and for 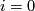 mod
mod  there are countably many such bundles.
there are countably many such bundles.
Remark 2.1. I find it remarkable that Bott doesn't mention the relation to vector bundles. Actually Bott does not say a single word, why his result is interesting. He obviously assumes that a reader finds the problem to determine the homotopy groups of such fundamental objects like the stable orthogonal or unitary group interesting in itself and he is of course right. Whether he has foreseen that it is such a fundamental result would be interesting to know, perhaps his friends Atiyah and Hirzebruch can comment on this.
3 The dates and dates of background papers
The paper with complete proofs appeared in September 1959, it was submitted November 1958. An announcement containing the above statements appeared in 1957 [Bott1957]. The methods of the proof were developed in several earlier papers [Bott1954], [Bott 1956].
4 The role of Bott periodicity for Kervaire-Milnor's paper
I hope there will be many articles in the atlas explaining more or less immediate applications of the periodicity theorem. Here I comment on the role it played in Kervaire and Milnor's important paper "Groups of homotopy spheres I" [Kervaire&Milnor1963]. This paper appeared May 1963, and was submitted April 1962. By that time the periodicity theorem must have been a standard tool in topology.
A smooth manifold homotopy equivalent to a sphere is called a homotopy sphere. Such manifolds are interesting for many reasons, one of them is the Poincaré conjecture saying that all these manifolds are homeomorphic to the standard sphere. There are no obvious constructions of such manifolds. But Milnor [Milnor1956] constructed a series of  -dimensional manifolds which are all homeomorphic to the
-dimensional manifolds which are all homeomorphic to the  -sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
-sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
The Poincaré conjecture was proven by Smale, Stallings and Zeeman (references) for 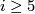 already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension
already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension  and by Perelmann [Perelman] in dimension
and by Perelmann [Perelman] in dimension  . Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
. Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
If  is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
Theorem [Kervaire-Milnor1963] 4.1. For all homotopy spheres  the stable tangent bundle is trivial.
the stable tangent bundle is trivial.
The proof of this theorem is based on three non-trivial theorems, one of which is Bott periodicity. This makes it in half of the cases a triviality, since for 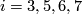 mod
mod  there is no non-trivial stable vector bundle over
there is no non-trivial stable vector bundle over  . The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over
. The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over  are isomorphic. Let's begin with the case
are isomorphic. Let's begin with the case 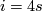 .
.
In the case 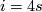 one has an invariant for stable vector bundles
one has an invariant for stable vector bundles  , namely the Pontrjagin classes
, namely the Pontrjagin classes 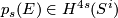 . It turns out that this map is a homomorphism from the stable vector bundles over
. It turns out that this map is a homomorphism from the stable vector bundles over 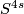 to
to 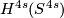 which by choosing an orientation we identify with
which by choosing an orientation we identify with  . Thus we have a homomorphism from a group isomorphic to
. Thus we have a homomorphism from a group isomorphic to  to
to  , and if it is non-trivial it is an injection implying that two stable vector bundles over
, and if it is non-trivial it is an injection implying that two stable vector bundles over 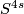 are isomorphic if and only their Pontrjagin classes
are isomorphic if and only their Pontrjagin classes 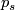 agree. To show that the homomorphism is non-trivial (for
agree. To show that the homomorphism is non-trivial (for  ) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
Kervaire and Milnor proceed slightly differently. They refer to obstruction theory, a theory which can be used to decide whether a vector bundle is trivial. They say (with reference to earlier papers by Kervaire) that the obstruction class and the Pontrjagin class 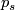 are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a
are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a 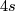 -dimensional homotopy sphere
-dimensional homotopy sphere  is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class
is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class 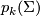 is a multiple of the signature
is a multiple of the signature 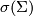 , which is zero since
, which is zero since 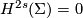 ."
."
Remark 4.2. Let me make a short comment on this sentence. It shows that the signature theorem, which was published by Hirzebruch in his 1956 book, is at the time when Kervaire and Milnor wrote their paper so standard, that neither a reference to Hirzebruch's book is needed (which appears in the list of references but no reference is given at this place) nor the formula of the signature theorem is repeated.
A non-trivial theorem is also needed in the remaining cases where 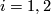 mod
mod  is. The cases
is. The cases  and
and  are trivial, but the higher dimensions not. Here the obstruction class sits in
are trivial, but the higher dimensions not. Here the obstruction class sits in 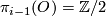 (by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form
(by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form  . There is a homomorphism introduced by Hopf-Whitehead (reference), the
. There is a homomorphism introduced by Hopf-Whitehead (reference), the 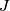 -homomorphism, from
-homomorphism, from 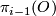 to the stable homotopy groups
to the stable homotopy groups 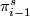 of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this
of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this 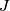 -homomorphism is injective.
-homomorphism is injective.
5 Some comments
After repeating the role of Bott periodicity in the proof of this theorem I would like to comment a bit on the role of this theorem in the paper of Kervaire and Milnor and in the further development of analyzing smooth structures on a topological manifold, here the sphere.
On the one hand the message of the theorem is negative, one cannot use the stable tangent bundle to distinguish different smooth structures on the sphere. This leads to the interesting question, whether the same is true for arbitrary manifolds. Later in the sixties some very deep theorems in this direction were proved.
On the other hand the theorem was a good start to develop a method to study the different smooth structures on spheres or equivalently the homotopy spheres in dimension 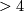 , a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds
, a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds  and
and  of dimension
of dimension 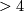 are diffeomorphic is to try to find an
are diffeomorphic is to try to find an  -cobordism between them, that is a compact manifold
-cobordism between them, that is a compact manifold  with boundary the disjoint union of
with boundary the disjoint union of  and
and  , such that the inclusions from
, such that the inclusions from  and
and  to
to  are homotopy equivalent (up to homotopy
are homotopy equivalent (up to homotopy  is cylinder). Then Smale's
is cylinder). Then Smale's  -cobordism theorem [Smale1961] implies that if the dimension of
-cobordism theorem [Smale1961] implies that if the dimension of  is larger than
is larger than  , then
, then  is diffeomorphic to the cylinder
is diffeomorphic to the cylinder ![M \times [0,1]](/images/math/b/2/e/b2eae1bd719f40c8fec914d995272cc8.png) , and so
, and so  and
and  are diffeomorphic.
are diffeomorphic.
Thus one tries to find an  -cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for
-cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for  . Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an
. Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an  -cobordism. They solve this problem completely by surgery theory.
-cobordism. They solve this problem completely by surgery theory.
Remark 5.1.
Suppose that a topological manifold  is given. Then one can ask whether
is given. Then one can ask whether  admits a smooth structure. A necessary condition is that
admits a smooth structure. A necessary condition is that  has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension
has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension 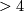 , but false in dimension
, but false in dimension  by the fundamental work of Donaldson (reference), and again true in dimension
by the fundamental work of Donaldson (reference), and again true in dimension 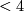 by different methods (Kirby-Sibenmann (reference)).
by different methods (Kirby-Sibenmann (reference)).
If we assume that  has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension
has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension 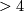 ). Roughly speaking the different smooth structures on
). Roughly speaking the different smooth structures on  correspond to the different ways to impose a stable tangent bundle on
correspond to the different ways to impose a stable tangent bundle on  (Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called
(Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called  -theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
-theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
6 References
- [Adams] Template:Adams
- [Atiyah-Hirzebruch] Template:Atiyah-Hirzebruch
- [Bott] Template:Bott
- [Bott 1956] Template:Bott 1956
- [Bott1954] Template:Bott1954
- [Bott1957] R. Bott, The stable homotopy of the classical groups, Proc. Nat. Acad. Sci. U.S.A. 43 (1957), 933–935. MR0102802 (21 #1588) Zbl 0129.15601
- [Bott1958] Template:Bott1958
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1958] Template:Kervaire&Milnor1958
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire-Milnor1963] Template:Kervaire-Milnor1963
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Perelman] Template:Perelman
- [Smale1961] S. Smale, Generalized Poincaré's conjecture in dimensions greater than four, Ann. of Math. (2) 74 (1961), 391–406. MR0137124 (25 #580) Zbl 0099.39202
- [Steenrod] Template:Steenrod
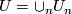 :
Thus one only needs to know the groups for small
:
Thus one only needs to know the groups for small  : For
: For 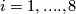 one has
one has 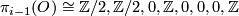
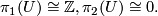
2 An interpretation in terms of vector bundles over spheres
Most applications of this result concern the interpretation of these groups as stable vector bundles over spheres. Namely if 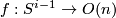 is a continuous map, then one obtains a vector bundle
is a continuous map, then one obtains a vector bundle 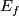 over
over 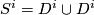 by taking two copies of
by taking two copies of 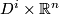 and by identifying
and by identifying 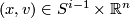 in the first copy with
in the first copy with 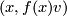 in the second copy. This map gives an isomorphism from
in the second copy. This map gives an isomorphism from 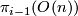 to the set
to the set 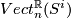 of isomorphism classes of
of isomorphism classes of  -dimensional vector bundles over
-dimensional vector bundles over  . I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly
. I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly 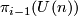 corresponds to the set
corresponds to the set 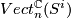 of isomorphism classes of complex
of isomorphism classes of complex  -dimensional vector bundles over
-dimensional vector bundles over  . Passing from
. Passing from  to
to 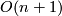 (or
(or 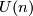 to
to 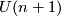 ) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the
) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the  -dimensional trivial bundle. By a general position argument the stabilization map is a bijection if
-dimensional trivial bundle. By a general position argument the stabilization map is a bijection if 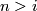 (
(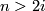 in the complex case). If
in the complex case). If 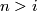 (or
(or 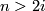 in the complex case) one calls such a bundle a stable vector bundle. Actually the
in the complex case) one calls such a bundle a stable vector bundle. Actually the  -dimensional vector bundles over
-dimensional vector bundles over  (not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for
(not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for 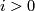 not equal to
not equal to 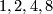 mod
mod  all real vector bundles of dimension
all real vector bundles of dimension 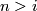 over
over  are trivial, that for
are trivial, that for 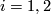 mod
mod  there are precisely
there are precisely  such bundles and for
such bundles and for 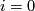 mod
mod  there are countably many such bundles.
there are countably many such bundles.
Remark 2.1. I find it remarkable that Bott doesn't mention the relation to vector bundles. Actually Bott does not say a single word, why his result is interesting. He obviously assumes that a reader finds the problem to determine the homotopy groups of such fundamental objects like the stable orthogonal or unitary group interesting in itself and he is of course right. Whether he has foreseen that it is such a fundamental result would be interesting to know, perhaps his friends Atiyah and Hirzebruch can comment on this.
3 The dates and dates of background papers
The paper with complete proofs appeared in September 1959, it was submitted November 1958. An announcement containing the above statements appeared in 1957 [Bott1957]. The methods of the proof were developed in several earlier papers [Bott1954], [Bott 1956].
4 The role of Bott periodicity for Kervaire-Milnor's paper
I hope there will be many articles in the atlas explaining more or less immediate applications of the periodicity theorem. Here I comment on the role it played in Kervaire and Milnor's important paper "Groups of homotopy spheres I" [Kervaire&Milnor1963]. This paper appeared May 1963, and was submitted April 1962. By that time the periodicity theorem must have been a standard tool in topology.
A smooth manifold homotopy equivalent to a sphere is called a homotopy sphere. Such manifolds are interesting for many reasons, one of them is the Poincaré conjecture saying that all these manifolds are homeomorphic to the standard sphere. There are no obvious constructions of such manifolds. But Milnor [Milnor1956] constructed a series of  -dimensional manifolds which are all homeomorphic to the
-dimensional manifolds which are all homeomorphic to the  -sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
-sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
The Poincaré conjecture was proven by Smale, Stallings and Zeeman (references) for 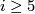 already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension
already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension  and by Perelmann [Perelman] in dimension
and by Perelmann [Perelman] in dimension  . Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
. Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
If  is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
Theorem [Kervaire-Milnor1963] 4.1. For all homotopy spheres  the stable tangent bundle is trivial.
the stable tangent bundle is trivial.
The proof of this theorem is based on three non-trivial theorems, one of which is Bott periodicity. This makes it in half of the cases a triviality, since for 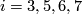 mod
mod  there is no non-trivial stable vector bundle over
there is no non-trivial stable vector bundle over  . The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over
. The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over  are isomorphic. Let's begin with the case
are isomorphic. Let's begin with the case 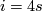 .
.
In the case 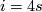 one has an invariant for stable vector bundles
one has an invariant for stable vector bundles  , namely the Pontrjagin classes
, namely the Pontrjagin classes 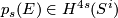 . It turns out that this map is a homomorphism from the stable vector bundles over
. It turns out that this map is a homomorphism from the stable vector bundles over 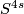 to
to 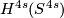 which by choosing an orientation we identify with
which by choosing an orientation we identify with  . Thus we have a homomorphism from a group isomorphic to
. Thus we have a homomorphism from a group isomorphic to  to
to  , and if it is non-trivial it is an injection implying that two stable vector bundles over
, and if it is non-trivial it is an injection implying that two stable vector bundles over 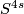 are isomorphic if and only their Pontrjagin classes
are isomorphic if and only their Pontrjagin classes 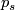 agree. To show that the homomorphism is non-trivial (for
agree. To show that the homomorphism is non-trivial (for  ) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
Kervaire and Milnor proceed slightly differently. They refer to obstruction theory, a theory which can be used to decide whether a vector bundle is trivial. They say (with reference to earlier papers by Kervaire) that the obstruction class and the Pontrjagin class 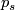 are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a
are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a 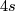 -dimensional homotopy sphere
-dimensional homotopy sphere  is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class
is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class 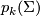 is a multiple of the signature
is a multiple of the signature 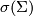 , which is zero since
, which is zero since 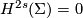 ."
."
Remark 4.2. Let me make a short comment on this sentence. It shows that the signature theorem, which was published by Hirzebruch in his 1956 book, is at the time when Kervaire and Milnor wrote their paper so standard, that neither a reference to Hirzebruch's book is needed (which appears in the list of references but no reference is given at this place) nor the formula of the signature theorem is repeated.
A non-trivial theorem is also needed in the remaining cases where 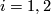 mod
mod  is. The cases
is. The cases  and
and  are trivial, but the higher dimensions not. Here the obstruction class sits in
are trivial, but the higher dimensions not. Here the obstruction class sits in 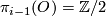 (by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form
(by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form  . There is a homomorphism introduced by Hopf-Whitehead (reference), the
. There is a homomorphism introduced by Hopf-Whitehead (reference), the 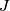 -homomorphism, from
-homomorphism, from 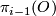 to the stable homotopy groups
to the stable homotopy groups 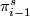 of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this
of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this 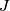 -homomorphism is injective.
-homomorphism is injective.
5 Some comments
After repeating the role of Bott periodicity in the proof of this theorem I would like to comment a bit on the role of this theorem in the paper of Kervaire and Milnor and in the further development of analyzing smooth structures on a topological manifold, here the sphere.
On the one hand the message of the theorem is negative, one cannot use the stable tangent bundle to distinguish different smooth structures on the sphere. This leads to the interesting question, whether the same is true for arbitrary manifolds. Later in the sixties some very deep theorems in this direction were proved.
On the other hand the theorem was a good start to develop a method to study the different smooth structures on spheres or equivalently the homotopy spheres in dimension 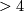 , a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds
, a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds  and
and  of dimension
of dimension 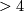 are diffeomorphic is to try to find an
are diffeomorphic is to try to find an  -cobordism between them, that is a compact manifold
-cobordism between them, that is a compact manifold  with boundary the disjoint union of
with boundary the disjoint union of  and
and  , such that the inclusions from
, such that the inclusions from  and
and  to
to  are homotopy equivalent (up to homotopy
are homotopy equivalent (up to homotopy  is cylinder). Then Smale's
is cylinder). Then Smale's  -cobordism theorem [Smale1961] implies that if the dimension of
-cobordism theorem [Smale1961] implies that if the dimension of  is larger than
is larger than  , then
, then  is diffeomorphic to the cylinder
is diffeomorphic to the cylinder ![M \times [0,1]](/images/math/b/2/e/b2eae1bd719f40c8fec914d995272cc8.png) , and so
, and so  and
and  are diffeomorphic.
are diffeomorphic.
Thus one tries to find an  -cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for
-cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for  . Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an
. Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an  -cobordism. They solve this problem completely by surgery theory.
-cobordism. They solve this problem completely by surgery theory.
Remark 5.1.
Suppose that a topological manifold  is given. Then one can ask whether
is given. Then one can ask whether  admits a smooth structure. A necessary condition is that
admits a smooth structure. A necessary condition is that  has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension
has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension 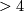 , but false in dimension
, but false in dimension  by the fundamental work of Donaldson (reference), and again true in dimension
by the fundamental work of Donaldson (reference), and again true in dimension 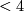 by different methods (Kirby-Sibenmann (reference)).
by different methods (Kirby-Sibenmann (reference)).
If we assume that  has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension
has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension 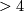 ). Roughly speaking the different smooth structures on
). Roughly speaking the different smooth structures on  correspond to the different ways to impose a stable tangent bundle on
correspond to the different ways to impose a stable tangent bundle on  (Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called
(Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called  -theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
-theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
6 References
- [Adams] Template:Adams
- [Atiyah-Hirzebruch] Template:Atiyah-Hirzebruch
- [Bott] Template:Bott
- [Bott 1956] Template:Bott 1956
- [Bott1954] Template:Bott1954
- [Bott1957] R. Bott, The stable homotopy of the classical groups, Proc. Nat. Acad. Sci. U.S.A. 43 (1957), 933–935. MR0102802 (21 #1588) Zbl 0129.15601
- [Bott1958] Template:Bott1958
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1958] Template:Kervaire&Milnor1958
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire-Milnor1963] Template:Kervaire-Milnor1963
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Perelman] Template:Perelman
- [Smale1961] S. Smale, Generalized Poincaré's conjecture in dimensions greater than four, Ann. of Math. (2) 74 (1961), 391–406. MR0137124 (25 #580) Zbl 0099.39202
- [Steenrod] Template:Steenrod
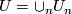 :
Thus one only needs to know the groups for small
:
Thus one only needs to know the groups for small  : For
: For 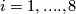 one has
one has 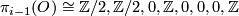
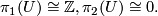
2 An interpretation in terms of vector bundles over spheres
Most applications of this result concern the interpretation of these groups as stable vector bundles over spheres. Namely if 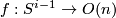 is a continuous map, then one obtains a vector bundle
is a continuous map, then one obtains a vector bundle 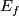 over
over 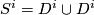 by taking two copies of
by taking two copies of 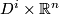 and by identifying
and by identifying 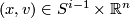 in the first copy with
in the first copy with 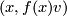 in the second copy. This map gives an isomorphism from
in the second copy. This map gives an isomorphism from 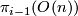 to the set
to the set 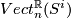 of isomorphism classes of
of isomorphism classes of  -dimensional vector bundles over
-dimensional vector bundles over  . I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly
. I don't know who observed this first, it can for example be found in Steenrod's book [Steenrod]. Similarly 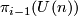 corresponds to the set
corresponds to the set 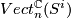 of isomorphism classes of complex
of isomorphism classes of complex  -dimensional vector bundles over
-dimensional vector bundles over  . Passing from
. Passing from  to
to 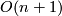 (or
(or 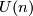 to
to 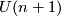 ) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the
) by the standard inclusion corresponds to stabilization of vector bundles by taking the Whitney sum with the  -dimensional trivial bundle. By a general position argument the stabilization map is a bijection if
-dimensional trivial bundle. By a general position argument the stabilization map is a bijection if 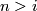 (
(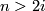 in the complex case). If
in the complex case). If 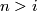 (or
(or 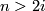 in the complex case) one calls such a bundle a stable vector bundle. Actually the
in the complex case) one calls such a bundle a stable vector bundle. Actually the  -dimensional vector bundles over
-dimensional vector bundles over  (not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for
(not over a general space) form an abelian group, where the sum is given by a connected sum of vector bundles: One choses a trivialization of the vector bundles over an open disk and identifies the resulting boundaries. Bott's theorem implies that for 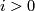 not equal to
not equal to 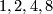 mod
mod  all real vector bundles of dimension
all real vector bundles of dimension 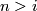 over
over  are trivial, that for
are trivial, that for 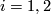 mod
mod  there are precisely
there are precisely  such bundles and for
such bundles and for 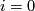 mod
mod  there are countably many such bundles.
there are countably many such bundles.
Remark 2.1. I find it remarkable that Bott doesn't mention the relation to vector bundles. Actually Bott does not say a single word, why his result is interesting. He obviously assumes that a reader finds the problem to determine the homotopy groups of such fundamental objects like the stable orthogonal or unitary group interesting in itself and he is of course right. Whether he has foreseen that it is such a fundamental result would be interesting to know, perhaps his friends Atiyah and Hirzebruch can comment on this.
3 The dates and dates of background papers
The paper with complete proofs appeared in September 1959, it was submitted November 1958. An announcement containing the above statements appeared in 1957 [Bott1957]. The methods of the proof were developed in several earlier papers [Bott1954], [Bott 1956].
4 The role of Bott periodicity for Kervaire-Milnor's paper
I hope there will be many articles in the atlas explaining more or less immediate applications of the periodicity theorem. Here I comment on the role it played in Kervaire and Milnor's important paper "Groups of homotopy spheres I" [Kervaire&Milnor1963]. This paper appeared May 1963, and was submitted April 1962. By that time the periodicity theorem must have been a standard tool in topology.
A smooth manifold homotopy equivalent to a sphere is called a homotopy sphere. Such manifolds are interesting for many reasons, one of them is the Poincaré conjecture saying that all these manifolds are homeomorphic to the standard sphere. There are no obvious constructions of such manifolds. But Milnor [Milnor1956] constructed a series of  -dimensional manifolds which are all homeomorphic to the
-dimensional manifolds which are all homeomorphic to the  -sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
-sphere (in particular homotopy equivalent) but some of which are not diffeomorphic to it. Such manifolds are called exotic spheres.
The Poincaré conjecture was proven by Smale, Stallings and Zeeman (references) for 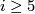 already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension
already before the paper by Kervaire and Milnor, and later by Freedman [Freedman1982] in dimension  and by Perelmann [Perelman] in dimension
and by Perelmann [Perelman] in dimension  . Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
. Thus the diffeomorphism classes of homotopy spheres correspond to the diffemorphism classes of smooth structures on the sphere.
If  is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
is a homotopy sphere one can ask for ways to distinguish it from the standard sphere. For example one could look at the stable tangent bundle, which for the standard sphere is trivial. Surprisingly this also holds for homotopy spheres:
Theorem [Kervaire-Milnor1963] 4.1. For all homotopy spheres  the stable tangent bundle is trivial.
the stable tangent bundle is trivial.
The proof of this theorem is based on three non-trivial theorems, one of which is Bott periodicity. This makes it in half of the cases a triviality, since for 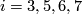 mod
mod  there is no non-trivial stable vector bundle over
there is no non-trivial stable vector bundle over  . The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over
. The remaining cases are not so easy, one needs a way to decide whether two stable vector bundles over  are isomorphic. Let's begin with the case
are isomorphic. Let's begin with the case 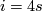 .
.
In the case 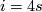 one has an invariant for stable vector bundles
one has an invariant for stable vector bundles  , namely the Pontrjagin classes
, namely the Pontrjagin classes 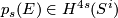 . It turns out that this map is a homomorphism from the stable vector bundles over
. It turns out that this map is a homomorphism from the stable vector bundles over 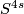 to
to 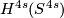 which by choosing an orientation we identify with
which by choosing an orientation we identify with  . Thus we have a homomorphism from a group isomorphic to
. Thus we have a homomorphism from a group isomorphic to  to
to  , and if it is non-trivial it is an injection implying that two stable vector bundles over
, and if it is non-trivial it is an injection implying that two stable vector bundles over 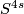 are isomorphic if and only their Pontrjagin classes
are isomorphic if and only their Pontrjagin classes 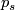 agree. To show that the homomorphism is non-trivial (for
agree. To show that the homomorphism is non-trivial (for  ) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
) one needs a single example where this is the case. Such examples where for example constructed by Borel and Hirzebruch (reference).
Kervaire and Milnor proceed slightly differently. They refer to obstruction theory, a theory which can be used to decide whether a vector bundle is trivial. They say (with reference to earlier papers by Kervaire) that the obstruction class and the Pontrjagin class 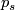 are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a
are proportional by a non-zero factor and so, if the Pontrjagin class is trivial, the bundle is trivial. They finish the argument that the stable tangent bundle of a 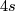 -dimensional homotopy sphere
-dimensional homotopy sphere  is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class
is trivial by one sentence: "But by the Hirzebruch signature theorem the Pontrjagin class 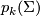 is a multiple of the signature
is a multiple of the signature 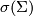 , which is zero since
, which is zero since 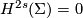 ."
."
Remark 4.2. Let me make a short comment on this sentence. It shows that the signature theorem, which was published by Hirzebruch in his 1956 book, is at the time when Kervaire and Milnor wrote their paper so standard, that neither a reference to Hirzebruch's book is needed (which appears in the list of references but no reference is given at this place) nor the formula of the signature theorem is repeated.
A non-trivial theorem is also needed in the remaining cases where 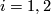 mod
mod  is. The cases
is. The cases  and
and  are trivial, but the higher dimensions not. Here the obstruction class sits in
are trivial, but the higher dimensions not. Here the obstruction class sits in 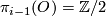 (by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form
(by Bott's theorem) and so again one has to find a way to distinguish the non-trivial element form  . There is a homomorphism introduced by Hopf-Whitehead (reference), the
. There is a homomorphism introduced by Hopf-Whitehead (reference), the 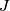 -homomorphism, from
-homomorphism, from 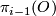 to the stable homotopy groups
to the stable homotopy groups 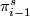 of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this
of spheres. Rohlin (reference) has shown that under this homomorphism the obstruction class vanishes (the authors don't give a reference to a paper by Rohlin but refer instead to an earlier paper by them [Kervaire&Milnor1958]). The argument, that also in the remaining case the stable tangent bundle is trivial is finished by applying a recent deep theorem by Adams [Adams] saying that this 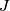 -homomorphism is injective.
-homomorphism is injective.
5 Some comments
After repeating the role of Bott periodicity in the proof of this theorem I would like to comment a bit on the role of this theorem in the paper of Kervaire and Milnor and in the further development of analyzing smooth structures on a topological manifold, here the sphere.
On the one hand the message of the theorem is negative, one cannot use the stable tangent bundle to distinguish different smooth structures on the sphere. This leads to the interesting question, whether the same is true for arbitrary manifolds. Later in the sixties some very deep theorems in this direction were proved.
On the other hand the theorem was a good start to develop a method to study the different smooth structures on spheres or equivalently the homotopy spheres in dimension  , a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds
, a method which in the following years was generalized to arbitrary manifolds. This is not the place to describe this method, which is called surgery theory. But the following can be said. The most successful way to decide whether two closed smooth simply connected manifolds  and
and  of dimension
of dimension  are diffeomorphic is to try to find an
are diffeomorphic is to try to find an  -cobordism between them, that is a compact manifold
-cobordism between them, that is a compact manifold  with boundary the disjoint union of
with boundary the disjoint union of  and
and  , such that the inclusions from
, such that the inclusions from  and
and  to
to  are homotopy equivalent (up to homotopy
are homotopy equivalent (up to homotopy  is cylinder). Then Smale's
is cylinder). Then Smale's  -cobordism theorem [Smale1961] implies that if the dimension of
-cobordism theorem [Smale1961] implies that if the dimension of  is larger than
is larger than  , then
, then  is diffeomorphic to the cylinder
is diffeomorphic to the cylinder ![M \times [0,1]](/images/math/b/2/e/b2eae1bd719f40c8fec914d995272cc8.png) , and so
, and so  and
and  are diffeomorphic.
are diffeomorphic.
Thus one tries to find an  -cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for
-cobordism between two homotopy spheres. Since the stable tangent bundle of the homotopy spheres is trivial the same holds for  . Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an
. Thus one can ask a weaker question, namely whether there is any bordism between the two homotopy spheres which has trivial stable tangent bundle. This is equivalent to a question in the stable homotopy groups of spheres, thus a very difficult question, but it is an unavoidable problem. If such a bordism exists Kervaire and Milnor try to improve it until it is an  -cobordism. They solve this problem completely by surgery theory.
-cobordism. They solve this problem completely by surgery theory.
Remark 5.1.
Suppose that a topological manifold  is given. Then one can ask whether
is given. Then one can ask whether  admits a smooth structure. A necessary condition is that
admits a smooth structure. A necessary condition is that  has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension
has a tangent bundle, and since this is easier to analyze and essentially the same, that it has a stable tangent bundle. It turns out that in a certain sense, which should be made precise elsewhere, this is the only obstruction, again in dimension 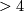 , but false in dimension
, but false in dimension  by the fundamental work of Donaldson (reference), and again true in dimension
by the fundamental work of Donaldson (reference), and again true in dimension 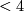 by different methods (Kirby-Sibenmann (reference)).
by different methods (Kirby-Sibenmann (reference)).
If we assume that  has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension
has a smooth structure, we choose one and compare all possible other smooth structures with this. Then again the stable tangent bundle plays the deciding role (in dimension 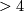 ). Roughly speaking the different smooth structures on
). Roughly speaking the different smooth structures on  correspond to the different ways to impose a stable tangent bundle on
correspond to the different ways to impose a stable tangent bundle on  (Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called
(Kirby-Sibenmann (reference)). Thus the understanding of stable vector bundles is what at the end is needed. This is the content of a very important theory, called  -theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
-theory, invented by Atiyah and Hirzebruch [Atiyah-Hirzebruch]. This is a generalized cohomology theory (meaning that the Eilenberg-Steenrod axioms for ordinary cohomology are fulfilled except the dimension axiom). This is the first generalized cohomology theory and - besides stable homotopy - the most important one. To construct it is up to a certain point rather elementary. But then one comes at a point where the arguments are highly non-trivial and the central tool, which one has to apply, is Bott perodicity. It does not only give the fundamental input for completing the proof that it is a generalized homology theory, it also is the central tool for all computations. In particular, in the few cases where one can give detailed information about the different smooth structures on a manifold, always Bott's theorem is in the background - like we indicated in one aspect for the spheres.
6 References
- [Adams] Template:Adams
- [Atiyah-Hirzebruch] Template:Atiyah-Hirzebruch
- [Bott] Template:Bott
- [Bott 1956] Template:Bott 1956
- [Bott1954] Template:Bott1954
- [Bott1957] R. Bott, The stable homotopy of the classical groups, Proc. Nat. Acad. Sci. U.S.A. 43 (1957), 933–935. MR0102802 (21 #1588) Zbl 0129.15601
- [Bott1958] Template:Bott1958
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1958] Template:Kervaire&Milnor1958
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire-Milnor1963] Template:Kervaire-Milnor1963
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Perelman] Template:Perelman
- [Smale1961] S. Smale, Generalized Poincaré's conjecture in dimensions greater than four, Ann. of Math. (2) 74 (1961), 391–406. MR0137124 (25 #580) Zbl 0099.39202
- [Steenrod] Template:Steenrod