Borel Conjecture for compact aspherical 4-manifolds
[edit] 1 Problem
Let  and
and  be a compact aspherical
be a compact aspherical  -manifolds with boundary. The Borel Conjecture in this setting
states that a homotopy equivalence of pairs
-manifolds with boundary. The Borel Conjecture in this setting
states that a homotopy equivalence of pairs 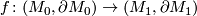 which is a homeomorphism
on the boundary is homotopic, relative to the boundary, to a homeomorphism.
which is a homeomorphism
on the boundary is homotopic, relative to the boundary, to a homeomorphism.
To apply topological surgery to attack this conjecture, assume that the fundamental group 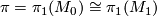 is good. One now proceeds to the following problems:
is good. One now proceeds to the following problems:
- Decide which good
 are the fundamental groups of compact
are the fundamental groups of compact  -manifolds.
-manifolds.
- Determine the homeomorphism type of the boundaries which can occur for each group in Part 1.
- For a fixed boundary and
 , prove the conjecture via surgery and the Farrell-Jones Conjecture
, prove the conjecture via surgery and the Farrell-Jones Conjecture
One can of course formulate the above in the smooth category. There are no known smooth counterexamples for closed manifolds; in particular, there is no known exotic smooth structure on 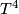 . There are smooth counterexamples for manifolds with boundary; in particular, see Akbulut, "A fake compact contractible 4-manifold."
. There are smooth counterexamples for manifolds with boundary; in particular, see Akbulut, "A fake compact contractible 4-manifold."
This problem was posed by Jim Davis, following discussions with Jonathan Hillman, Monday January 14th at MATRIX.