B-Bordism
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
On this page we recall the definition of the bordism groups of closed smooth manifolds, with extra topological structure: orientation, spin-structure, weakly almost complex structure etc. The situation for piecewise linear and topological manifolds is similar and we discuss it briefly below.
The formulation of the general set-up for B-Bordism dates back to [Lashof1963]. There are detailed treatments in [Stong1968, Chapter II] and [Bröcker&tom Dieck1970] as well as summaries in [Teichner1992, Part 1: 1], [Kreck1999, Section 1], [Kreck&Lück2005, 18.10]. See also the Wikipedia bordism page.
We specify extra topological structure universally by means of a fibration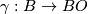 where
where 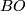 denotes the classifying space of the stable orthogonal group and
denotes the classifying space of the stable orthogonal group and  is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes
is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes  for the fibration
for the fibration 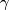 . Speaking somewhat imprecisely (precise details are below) a
. Speaking somewhat imprecisely (precise details are below) a  -manifold is a compact manifold
-manifold is a compact manifold Tex syntax errortogether with a lift to
 of a classifying map for the stable normal bundle of
of a classifying map for the stable normal bundle of Tex syntax error:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ W \ar[r]^{\nu_W} \ar[ur]^{\bar \nu} & BO.}](/images/math/8/1/a/81ae570ccbeade1a8c09ffd94737a3f1.png)
The  -dimensional
-dimensional  -bordism group is defined to be the set of closed
-bordism group is defined to be the set of closed  -manifolds modulo the relation of bordism via compact
-manifolds modulo the relation of bordism via compact  -manifolds. Addition is given by disjoint union and in fact for each
-manifolds. Addition is given by disjoint union and in fact for each  there is a group
there is a group
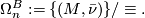
Alternative notations are 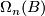 and also
and also 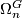 when
when 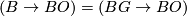 for
for 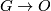 a stable representation of a topological group
a stable representation of a topological group  . Details of the definition and some important theorems for computing
. Details of the definition and some important theorems for computing 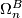 follow.
follow.
[edit] 1.1 Examples
We list some fundamental examples with common notation and also indicate the fibration B.
- Unoriented bordism:
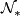 ;
; 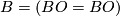 .
.
- Oriented bordism:
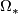 ,
, 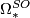 ;
; 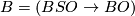 .
.
- Spin bordism:
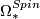 ;
; 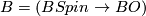 .
.
- Spin
 bordism:
bordism: 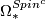 ;
; 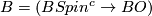 .
.
- String bodism :
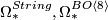 ;
; 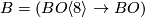 .
.
- Complex bordism :
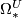 ;
; 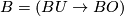 .
.
- Special unitary bordism :
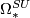 ;
; 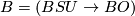 .
.
- Framed bordism :
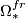 ;
; 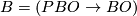 , the path space fibration.
, the path space fibration.
[edit] 2 B-structures and bordisms
In this section we give a compressed accont of parts of [Stong1968, Chapter II]. Let 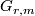 denote the Grassmann manifold of unoriented
denote the Grassmann manifold of unoriented  -planes in
-planes in  and let
and let 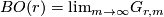 be the infinite Grassmannian and fix a fibration
be the infinite Grassmannian and fix a fibration 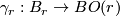 .
.
Definition 2.1.
Let 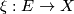 be a rank r vector bundle classified by
be a rank r vector bundle classified by 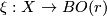 . A
. A 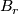 -structure on
-structure on  is a vertical homotopy class of maps
is a vertical homotopy class of maps 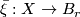 such that
such that 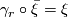 .
.
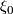 and
and 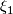 are isomorphic vector bundles over
are isomorphic vector bundles over  then the sets of
then the sets of 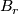 -structures on each are in bijective equivalence. However
-structures on each are in bijective equivalence. However 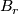 -structures are defined on specific bundles, not isomorphism classes of bundles: a specific isomorphism, up to appropriate equivalence, is required to give a bijection between the sets of
-structures are defined on specific bundles, not isomorphism classes of bundles: a specific isomorphism, up to appropriate equivalence, is required to give a bijection between the sets of 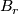 structures. Happily this is the case for the normal bundle of an embedding as we now explain. Let
structures. Happily this is the case for the normal bundle of an embedding as we now explain. Let Tex syntax errorbe a compact manifold and let
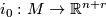 be an embedding. Equipping
be an embedding. Equipping 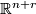 with the standard metric, the normal bundle of
with the standard metric, the normal bundle of 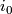 is a rank r vector bundle over
is a rank r vector bundle over Tex syntax errorclassified by its normal Gauss map
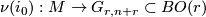 . If
. If 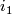 is another such embedding and
is another such embedding and 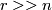 , then
, then 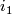 is regularly homotopic to
is regularly homotopic to 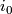 and all regular homotopies are regularly homotopic relative to their endpoints (see [Hirsch1959]). A regular homotopy
and all regular homotopies are regularly homotopic relative to their endpoints (see [Hirsch1959]). A regular homotopy  defines an isomorphism
defines an isomorphism 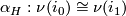 and a regular homotopy of regular homotopies gives a homotopy between these isomorphisms. Taking care one proves the following
and a regular homotopy of regular homotopies gives a homotopy between these isomorphisms. Taking care one proves the following
Lemma 2.2 [Stong1968, p 15].
For r sufficiently large, (depending only on n) there is a 1-1 correspondence between the set of 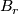 structures of the normal bundles of any two embeddings
structures of the normal bundles of any two embeddings  .
.
This lemma is one motivation for the useful but subtle notion of a fibred stable vector bundle.
Definition 2.3.
A fibred stable vector bundle  consists of the following data: a sequence of fibrations
consists of the following data: a sequence of fibrations 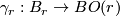 together with a sequence of maps
together with a sequence of maps 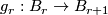 fitting into the following commutative diagram
fitting into the following commutative diagram
![\displaystyle \xymatrix{ B_r \ar[r]^{g_r} \ar[d]^{\gamma_r} & B_{r+1} \ar[d]^{\gamma_{r+1}} \\ BO(r) \ar[r]^{j_r} & BO(r+1) }](/images/math/7/c/1/7c1c615ec7ae50c39e222dd0f32582ad.png)
where 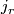 is the standard inclusion. We let
is the standard inclusion. We let 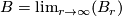 .
.
Remark 2.4.
A fibred stable vector bundle  gives rise to a stable vector bundle as defined in [Kreck&Lück2005, 18.10]. One defines
gives rise to a stable vector bundle as defined in [Kreck&Lück2005, 18.10]. One defines 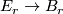 to be the pullback bundle
to be the pullback bundle 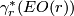 where
where 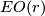 is the universal r-plane bundle over
is the universal r-plane bundle over 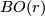 . The diagram above gives rise to bundle maps
. The diagram above gives rise to bundle maps 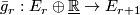 covering the maps
covering the maps 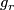 ; where
; where 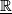 denotes the trivial rank 1 bundle over
denotes the trivial rank 1 bundle over 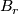 .
.
Now a 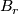 -structure on the normal bundle of an embedding
-structure on the normal bundle of an embedding 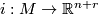 defines a unique
defines a unique 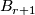 -structure on the composition of
-structure on the composition of  with the standard inclusion
with the standard inclusion 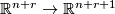 . Hence we can make the following
. Hence we can make the following
Definition 2.5 [Stong1968, p 15].
Let be a fibred stable vector bundle. A
be a fibred stable vector bundle. A  -structure on
-structure on Tex syntax erroris an equivalence class of
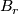 -structure on
-structure on Tex syntax errorwhere two such structures are equivalent if they become equivalent for r sufficiently large. A
 -manifold is a pair
-manifold is a pair 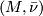 where
where Tex syntax erroris a compact manifold and
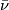 is a
is a  -structure on
-structure on Tex syntax error.
If  is a compact manifold with boundary
is a compact manifold with boundary 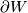 then by choosing the inward-pointing normal vector along
then by choosing the inward-pointing normal vector along 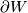 , a
, a  -structure on
-structure on  restricts to a
restricts to a  -structure on
-structure on 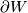 . In particular, if
. In particular, if 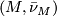 is a closed
is a closed  manifold then
manifold then ![W = M \times [0, 1]](/images/math/3/d/8/3d810ac2ba6ec7b778512bb115c679a1.png) has a canonical
has a canonical  -structure
-structure ![\bar \nu_{M \times [0, 1]}](/images/math/d/5/e/d5e27b479782bc34079dd44364fbde46.png) which restricts to
which restricts to 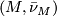 on
on 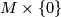 . The restriction of this
. The restriction of this  -structure to
-structure to 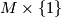 is denoted
is denoted  : by construction
: by construction 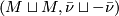 is the boundary of
is the boundary of ![(M \times [0, 1], \bar \nu_{M \times [0, 1]})](/images/math/2/1/1/211b7379908ebadefcfcb657255c97d5.png) .
.
Definition 2.6.
Closed  -manifolds
-manifolds 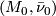 and
and 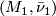 are
are  -bordant if there is a compact
-bordant if there is a compact  -manifold
-manifold 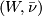 such that
such that 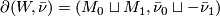 . We write
. We write ![[M, \bar \nu]](/images/math/3/0/2/30282bb5acfadbc45b3b2f90df238541.png) for the bordism class of
for the bordism class of 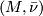 .
.
Proposition 2.7 [Stong1968, p 17].
The set of  -bordism classes of closed n-manifolds with
-bordism classes of closed n-manifolds with  -structure,
-structure,
![\displaystyle \Omega_n^B := \{ [M, \bar \nu ] \},](/images/math/0/e/c/0ec9d94e5d00beba3be787adfd09d089.png)
forms an abelian group under the operation of disjoint union with inverse ![-[M,\bar \nu] = [M, -\bar \nu]](/images/math/4/5/0/450ad56098e90f7f2f6b0b2b9e710fd2.png) .
.
[edit] 3 Singular bordism
 -bordism gives rise to a generalised homology theory. If
-bordism gives rise to a generalised homology theory. If  is a space then the
is a space then the  -cycles of this homology theory are pairs
-cycles of this homology theory are pairs
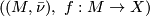
where 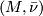 is a closed
is a closed  -dimensional
-dimensional  -manifold and
-manifold and  is any continuous map. Two cycles
is any continuous map. Two cycles 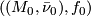 and
and 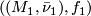 are homologous if there is a pair
are homologous if there is a pair
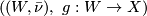
where 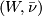 is a
is a  -bordism from
-bordism from 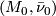 to
to 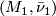 and
and 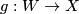 is a continuous map extending
is a continuous map extending 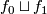 . Writing
. Writing ![[(M, \bar \nu), f]](/images/math/f/1/2/f12f2172f5992fd5f5196a4b1a8223a5.png) for the equivalence class of
for the equivalence class of 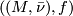 we obtain an abelian group
we obtain an abelian group
![\displaystyle \Omega_n^B(X) : = \{ [(M, \bar \nu), f] \}](/images/math/0/e/9/0e94afc4f128e412222f4c91e415ee41.png)
with group operation disjoint union and inverse ![-[(M, \bar \nu), f] = [(M, - \bar \nu), f]](/images/math/3/f/f/3ff574c2ae44f17cba23e0d71c725468.png) .
.
Proposition 3.1.
The mapping 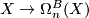 defines a generalised homology theory with coefficients
defines a generalised homology theory with coefficients 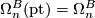 .
.
Given a stable vector bundle 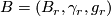 we can form the stable vector bundle
we can form the stable vector bundle 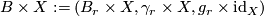 . The following simple lemma is clear but often useful.
. The following simple lemma is clear but often useful.
Lemma 3.2.
For any space  there is an isomorphism
there is an isomorphism 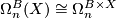 .
.
[edit] 4 The orientation homomorphism
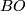 . It then follows that every closed
. It then follows that every closed  -manifold
-manifold 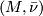 is given a local orientation. This amounts to a choice of fundamental class of
is given a local orientation. This amounts to a choice of fundamental class of Tex syntax errorwhich is a generator
![\displaystyle [M] \in H_n(M; \underline{\Zz})](/images/math/c/3/e/c3e19cf09ded2cfda7d3aef03e7a2198.png)
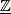 denotes the local coefficient system defined by the orientation character of
denotes the local coefficient system defined by the orientation character of Tex syntax error.
Given a closed  -manifold
-manifold 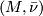 we can use
we can use 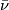 to push the fundamental class of
to push the fundamental class of ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) to
to ![\bar \nu_*[M] \in H_n(B; \underline{\Zz})](/images/math/a/2/9/a2993acb7bab6efb1654d1df8a51dbf7.png) . Now the local coefficient system is defined by the orientation character of the stable bundle
. Now the local coefficient system is defined by the orientation character of the stable bundle  . It is easy to check that
. It is easy to check that ![\bar \nu_*[M]](/images/math/3/f/a/3fae9c7af1aea3f0c8594ce2b27838c9.png) depends only on the
depends only on the  -bordism class of
-bordism class of 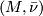 and is additive with respect to the operations
and is additive with respect to the operations 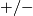 on
on 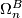 .
.
Definition 4.1.
Let  be a fibred stable vector bundle. The orientation homomorphism is defined as follows:
be a fibred stable vector bundle. The orientation homomorphism is defined as follows:
![\displaystyle \rho : \Omega_n^B \to H_n(B; \underline{\Zz}), ~~~[M, \bar \nu] \mapsto \bar \nu_*[M].](/images/math/a/b/3/ab3eb885589c82b5a77ff4fccdf229bd.png)
For the singular bordism groups 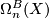 we have no bundle over
we have no bundle over  so in general there is only a
so in general there is only a 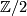 -valued orientation homomorphism. However, if the first Stiefel-Whitney class of
-valued orientation homomorphism. However, if the first Stiefel-Whitney class of  vanishes,
vanishes, 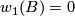 , then all
, then all  -manifolds are oriented in the usual sense and the orientation homomorphism can be lifted to
-manifolds are oriented in the usual sense and the orientation homomorphism can be lifted to  .
.
Definition 4.2.
Let  be a fibred stable vector bundle. The orientation homomorphism in singular bordism is defined as follows:
be a fibred stable vector bundle. The orientation homomorphism in singular bordism is defined as follows:
![\displaystyle \rho : \Omega_n^B(X) \to H_n(X; \Zz/2), ~~~ [(M, \bar \nu), f] \mapsto f_*[M].](/images/math/e/6/4/e644fe719a7dc5162365ab6cf4e4b462.png)
If 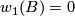 then for all closed
then for all closed  -manifolds
-manifolds ![[M] \in H_n(M; \Zz)](/images/math/4/f/8/4f8b47275404f2ddfa8f929bf709ea6e.png) and we can replace the
and we can replace the 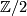 -coefficients with
-coefficients with  -coefficients above.
-coefficients above.
[edit] 5 The Pontrjagin-Thom isomorphism
If  is a vector bundle, let
is a vector bundle, let 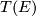 denote its Thom space. Recall that that a fibred stable vector bundle
denote its Thom space. Recall that that a fibred stable vector bundle 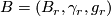 defines a stable vector bundle
defines a stable vector bundle 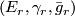 where
where 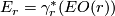 . This stable vector bundle defines a Thom spectrum which we denote
. This stable vector bundle defines a Thom spectrum which we denote 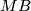 . The
. The  -th space of
-th space of 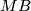 is
is 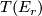 .
.
By definition a  -manifold,
-manifold, 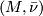 , is an equivalence class of
, is an equivalence class of 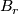 -structures on
-structures on 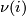 , the normal bundle of an embedding
, the normal bundle of an embedding 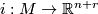 . Hence
. Hence 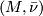 gives rise to the collapse map
gives rise to the collapse map
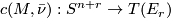
where we identify  with the one-point compatificiation of
with the one-point compatificiation of 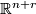 , we map via
, we map via 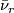 on a tubular neighbourhood of
on a tubular neighbourhood of 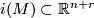 and we map all other points to the base-point of
and we map all other points to the base-point of 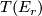 . As r increases these maps are compatibly related by suspension and the structure maps of the spectrum
. As r increases these maps are compatibly related by suspension and the structure maps of the spectrum 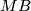 . Hence we obtain a homotopy class
. Hence we obtain a homotopy class
![\displaystyle [c(M, \bar \nu)] =: P((M, \bar \nu)) \in \text{lim}_{r \to \infty}(\pi_{n+r}(T(E_r)) = \pi_n(MB).](/images/math/a/9/6/a962b5a6499a87420e136c4030c0aa0f.png)
The celebrated theorem of Pontrjagin and Thom states in part that 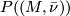 depends only on the bordism class of
depends only on the bordism class of 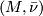 .
.
Theorem 5.1. There is an isomorphism of abelian groups
![\displaystyle P : \Omega_n^B \cong \pi_n^S(MB), ~~~[M, \bar \nu] \longmapsto P([M, \bar \nu]).](/images/math/b/5/d/b5dde7798ff8542a4d3599c261e28840.png)
For the proof see [Bröcker&tom Dieck1970, Satz 3.1 and Satz 4.9].
For example, if 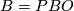 is the path fibration over
is the path fibration over 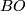 , then
, then 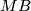 is homotopic to the sphere spectrum
is homotopic to the sphere spectrum 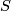 and
and 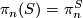 is the
is the  -th stable homotopy group. On the other hand, in this case
-th stable homotopy group. On the other hand, in this case 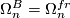 is the framed bordism group and as a special case of Theorem 5.1 we have
is the framed bordism group and as a special case of Theorem 5.1 we have
Theorem 5.2.
There is an isomorphism 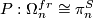 .
.
The Pontrjagin-Thom isomorphism generalises to singular bordism.
Theorem 5.3.
For any space  there is an isomorphism of abelian groups
there is an isomorphism of abelian groups
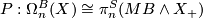
where 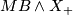 denotes the smash produce of the specturm
denotes the smash produce of the specturm 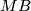 and the space
and the space  with a disjoint basepoint added.
with a disjoint basepoint added.
[edit] 6 Spectral sequences
For any generalised homology theory 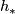 there is a spectral sequence, called the Atiyah-Hirzebruch spectral sequence (AHSS) which can be used to compute
there is a spectral sequence, called the Atiyah-Hirzebruch spectral sequence (AHSS) which can be used to compute 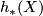 . The
. The 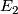 term of the AHSS is
term of the AHSS is 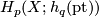 and one writes
and one writes
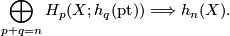
The Pontrjagin-Thom isomorphisms above therefore give rise to the following theorems. For the first we recall that stable homotopy defines a generalised homology theory, and we use the Thom isomorphism with local coefficients: 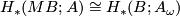 .
.
Theorem 6.1.
Let  be a fibred stable vector bundle. There is a spectral sequence
be a fibred stable vector bundle. There is a spectral sequence
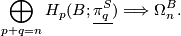
Theorem 6.2.
Let  be a fibred stable vector bundle and
be a fibred stable vector bundle and  a space. There is a spectral sequence
a space. There is a spectral sequence
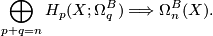
Next recall Serre's theorem [Serre1951] that 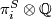 vanishes unless
vanishes unless 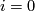 in which case
in which case 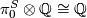 . From the above spectral sequences of Theorems 6.1 and 6.2 we deduce the following
. From the above spectral sequences of Theorems 6.1 and 6.2 we deduce the following
Theorem 6.3 Cf. [Kreck&Lück2005, Thm 2.1].
If 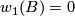 then the orientation homomorphism induces an isomorphism
then the orientation homomorphism induces an isomorphism
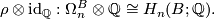
Moreover for any space  ,
, 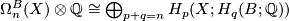 and if
and if  is connected, the rationalised orientation homomorphism
is connected, the rationalised orientation homomorphism 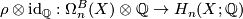 may be identified with the projection
may be identified with the projection
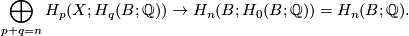
[edit] 7 Piecewise linear and topological bordism
Let 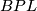 and
and 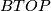 denote respectively the classifying spaces for stable piecewise linear homeomorphisms of Euclidean space and origin-preserving homeomorphisms of Euclidean space. Note that while there are honest groups
denote respectively the classifying spaces for stable piecewise linear homeomorphisms of Euclidean space and origin-preserving homeomorphisms of Euclidean space. Note that while there are honest groups 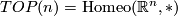 and
and 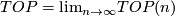 , the piecewise linear case requires more care.
, the piecewise linear case requires more care.
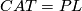 or
or 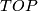 , and
, and 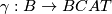 is a fibration, and
is a fibration, and Tex syntax erroris a compact
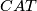 manifold then just as above, we can define an
manifold then just as above, we can define an  -structure on
-structure on Tex syntax errorto be an equivalence class of lifts of of the classifying map of the stable normal bundle of
Tex syntax error:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ M \ar[r]^{\nu_M} \ar[ur]^{\bar \nu} & BCAT.}](/images/math/2/5/6/25665d34c39306a05bbf87ebdf4c3f6a.png)
Note that 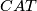 manifolds have stable normal
manifolds have stable normal 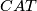 bundles classified by
bundles classified by 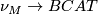 .
.
Just as before we obtain bordism groups 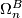 of closed n-dimensional
of closed n-dimensional 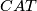 -manifolds with
-manifolds with  structure
structure
![\displaystyle \Omega_n^B : = \{ [M, \bar \nu ]\}.](/images/math/2/a/f/2af6e1e7c515cfbc5e15df8f55f9cf1a.png)
The fibration  again defines a Thom spectrum
again defines a Thom spectrum 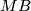 and one asks if there is a Pontrjagin-Thom isomorphism. The proof of the Pontrjagin-Thom theorem relies on transversality for manifolds and while this is comparatively easy in the
and one asks if there is a Pontrjagin-Thom isomorphism. The proof of the Pontrjagin-Thom theorem relies on transversality for manifolds and while this is comparatively easy in the 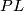 -category, it is was a major breakthrough to achieve this for topological manifolds: achieved in [Kirby&Siebenmann1977] for dimensions other than 4 and then in [Freedman&Quinn1990] in dimension 4. Thus one has
-category, it is was a major breakthrough to achieve this for topological manifolds: achieved in [Kirby&Siebenmann1977] for dimensions other than 4 and then in [Freedman&Quinn1990] in dimension 4. Thus one has
Theorem 7.1.
There is an isomorphism 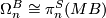 .
.
The basic bordism groups for 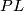 and
and  manifolds,
manifolds, 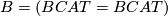 and
and 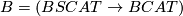 , are denoted by
, are denoted by 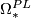 ,
, 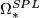 ,
, 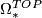 and
and 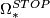 . Their computation is significantly more difficult than the corresponding bordism groups of smooth manifolds: there is no analogue of Bott periodicity for
. Their computation is significantly more difficult than the corresponding bordism groups of smooth manifolds: there is no analogue of Bott periodicity for 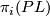 and
and 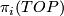 and so the spectra
and so the spectra 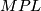 and
and 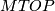 are far more complicated. For now we simply refer the reader to [Madsen&Milgram1979, Chapters 5 & 14] and [Brumfiel&Madsen&Milgram1973].
are far more complicated. For now we simply refer the reader to [Madsen&Milgram1979, Chapters 5 & 14] and [Brumfiel&Madsen&Milgram1973].
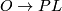 and
and 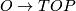 induce isomorphisms
induce isomorphisms 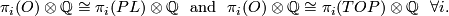
As a consequence one has
Theorem 7.2. There are isomorphisms
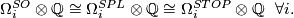
[edit] 8 References
- [Brumfiel&Madsen&Milgram1973] G. Brumfiel, I. Madsen and R. J. Milgram,
 characteristic classes and cobordism, Ann. of Math. (2) 97 (1973), 82–159. MR0310881 (46 #9979) Zbl 0248.57006
characteristic classes and cobordism, Ann. of Math. (2) 97 (1973), 82–159. MR0310881 (46 #9979) Zbl 0248.57006
- [Bröcker&tom Dieck1970] T. Bröcker and T. tom Dieck, Kobordismentheorie, Springer-Verlag, Berlin, 1970. MR0275446 (43 #1202) Zbl 0211.55501
- [Freedman&Quinn1990] M. H. Freedman and F. Quinn, Topology of 4-manifolds, Princeton University Press, Princeton, NJ, 1990. MR1201584 (94b:57021) Zbl 0705.57001
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Lashof1963] R. Lashof, Poincaré duality and cobordism, Trans. Amer. Math. Soc. 109 (1963), 257–277. MR0156357 (27 #6281) Zbl 0137.42803
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Serre1951] J. Serre, Homologie singulière des espaces fibrès. Applications, Ann. of Math. (2) 54 (1951), 425–505. MR0045386 (13,574g) Zbl 0045.26003
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
- [Teichner1992] P. Teichner, Topological 4-manifolds with finite fundamental group PhD Thesis, University of Mainz, Germany, Shaker Verlag 1992, ISBN 3-86111-182-9.