Algebraic mapping cone

Revision as of 15:27, 6 June 2012

Definition

Let $<wikitex>; == Definition == Let $E \xrightarrow{f} F$ be a map of chain complexes. Define the ''algebraic mapping cone of'' $f$ as a chain complex $Cone(f)$ given in degree $k$ by $$ Cone(f)_k=E_{k-1}\oplus F_k $$ with differential $$ \partial_{Cone(f)}= \left( \begin{array}{cc} -\partial_E & 0 \ f & \partial_F \end{array} \right) : Cone(f)_k\rightarrow Cone(f)_{k-1}. $$ Every book on homological algebra contains this definition, except for the sign conventions in the differentials! For example, it is possible to have $$ \partial_{Cone(f)}= \left( \begin{array}{cc} \partial_E & 0 \ (-)^kf & \partial_F \end{array} \right) : Cone(f)_k\rightarrow Cone(f)_{k-1}. $$ A good source is for example \cite{Weibel1994}. 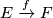</wikitex> == References == {{#RefList:}}E \xrightarrow{f} F$ be a map of chain complexes. 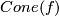Define the algebraic mapping cone of $f$ as a chain complex $Cone(f)$ given in degree $k$ by

$$\displaystyle Cone(f)_k=E_{k-1}\oplus F_k$$

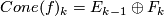
with differential

$$\displaystyle \partial_{Cone(f)}= \left( \begin{array}{cc} -\partial_E & 0 \\ f & \partial_F \end{array} \right) : Cone(f)_k\rightarrow Cone(f)_{k-1}.$$

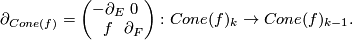
Every book on homological algebra contains this definition, except for the sign conventions in the differentials! For example, it is possible to have

$$\displaystyle \partial_{Cone(f)}= \left( \begin{array}{cc} \partial_E & 0 \\ (-)^kf & \partial_F \end{array} \right) : Cone(f)_k\rightarrow Cone(f)_{k-1}.$$

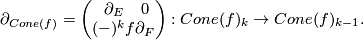
A good source is for example [Weibel1994].

References

• [Weibel1994] C. A. Weibel, An introduction to homological algebra, Cambridge University Press, 1994. MR1269324 (95f:18001) Zbl 0834.18001