5-manifolds with fundamental group of order 2
(→Construction and examples) |
Marek Kaluba (Talk | contribs) m (→Introduction) |
||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | The classification of simply-connected 5-manifolds was achieved by Smale \cite{Smale} and Barden \cite{Barden} in the 1960s. The surgery and modified surgery theories provide a toolkit to attack the classification problem of high dimensional manifolds. Dimension 5 is the lowest dimension where the theories apply (except for the 4-dimensional TOP-category), therefore an understanding of the classification of 5-manifolds beyond the Smale-Barden results is expectable. On the other hand, it's known (\cite{Markov}, \cite{Kervaire}) that every finitely generated group can be realized as the fundamental group of a manifold of dimension $\ge$ 4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental in advance and consider the classification of manifolds with the given fundamental group. | + | The classification of simply-connected 5-manifolds was achieved by Smale \cite{Smale} and Barden \cite{Barden} in the 1960s. The surgery and modified surgery theories provide a toolkit to attack the classification problem of high dimensional manifolds. Dimension 5 is the lowest dimension where the theories apply (except for the 4-dimensional TOP-category), therefore an understanding of the classification of 5-manifolds beyond the Smale-Barden results is expectable. On the other hand, it's known (\cite{Markov}, \cite{Kervaire}) that every finitely generated group can be realized as the fundamental group of a manifold of dimension $\ge$ 4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental group in advance and consider the classification of manifolds with the given fundamental group. |
From this point of view, the fist step one might take is the group $\Zz_2$, which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group $\Zz$ is the simplest one.) | From this point of view, the fist step one might take is the group $\Zz_2$, which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group $\Zz$ is the simplest one.) | ||
| − | + | Any other point one should take into account concerning the classification of manifolds with nontrivial fundamental groups $\pi_1$ is that the higher homotopy groups $\pi_i$ ($i \ge 2$) are modules over the group ring $\Zz[\pi_1]$, which are apparently homotopy invariants. Especially when we consider $5$-manifolds $M^5$, the $\Zz[\pi_1]$-module structure of $\pi_2(M)$ will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case. | |
Most part of this item will be a survey of the classification result of 5-manifolds $M^5$ with fundamental group $\pi_1(M)=\Zz_2$, $\pi_2(M)$ torsion free and is a trivial $\Zz[\Zz_2]$-module obtained in \cite{Hambleton&Su} . | Most part of this item will be a survey of the classification result of 5-manifolds $M^5$ with fundamental group $\pi_1(M)=\Zz_2$, $\pi_2(M)$ torsion free and is a trivial $\Zz[\Zz_2]$-module obtained in \cite{Hambleton&Su} . | ||
Latest revision as of 02:36, 7 February 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
The classification of simply-connected 5-manifolds was achieved by Smale [Smale] and Barden [Barden] in the 1960s. The surgery and modified surgery theories provide a toolkit to attack the classification problem of high dimensional manifolds. Dimension 5 is the lowest dimension where the theories apply (except for the 4-dimensional TOP-category), therefore an understanding of the classification of 5-manifolds beyond the Smale-Barden results is expectable. On the other hand, it's known ([Markov], [Kervaire]) that every finitely generated group can be realized as the fundamental group of a manifold of dimension  4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental group in advance and consider the classification of manifolds with the given fundamental group.
4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental group in advance and consider the classification of manifolds with the given fundamental group.
From this point of view, the fist step one might take is the group  , which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group
, which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group  is the simplest one.)
is the simplest one.)
Any other point one should take into account concerning the classification of manifolds with nontrivial fundamental groups 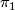 is that the higher homotopy groups
is that the higher homotopy groups 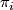 (
(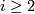 ) are modules over the group ring
) are modules over the group ring ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) , which are apparently homotopy invariants. Especially when we consider
, which are apparently homotopy invariants. Especially when we consider 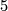 -manifolds
-manifolds 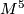 , the
, the ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) -module structure of
-module structure of 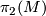 will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
Most part of this item will be a survey of the classification result of 5-manifolds 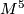 with fundamental group
with fundamental group 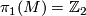 ,
, 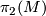 torsion free and is a trivial
torsion free and is a trivial ![\Zz[\Zz_2]](/images/math/0/6/e/06e45b437bee7ce0e2224a3e03e368b4.png) -module obtained in [Hambleton&Su] .
-module obtained in [Hambleton&Su] .
[edit] 2 Construction and examples
First some examples known from other context.
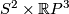 ;
;
-
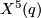
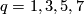 are the 5-dimensional fake real projective spaces with
are the 5-dimensional fake real projective spaces with 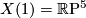 (There are exactly 4 in the smooth category). The meaning of
(There are exactly 4 in the smooth category). The meaning of  will be clear in the section ``Invariants".
will be clear in the section ``Invariants".
[edit] 2.1 Circle bundles over simply-connected 4-manifolds
Let 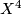 be a closed simply-connected topological 4-manifold,
be a closed simply-connected topological 4-manifold,  be a complex line bundle over
be a complex line bundle over  with Chern class
with Chern class 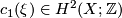 . Let the divisibility of
. Let the divisibility of 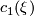 be
be  (i.e.
(i.e. 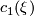 is
is  multiple of a primitive element in
multiple of a primitive element in 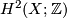 , then the sphere bundle
, then the sphere bundle 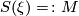 is a 5-manifold with fundament group
is a 5-manifold with fundament group 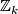 and
and 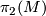 is a free abelian group of rank
is a free abelian group of rank 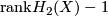 , and
, and 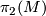 is a trivial module over the group ring. A priori
is a trivial module over the group ring. A priori  is a topological manifold. The smoothing problem is addressed by the following
is a topological manifold. The smoothing problem is addressed by the following
Proposition 2.1.[Hambleton&Su, Proposition 4.2]
Assume  is nontrivial. If
is nontrivial. If  is odd, then
is odd, then  admits a smooth structure; if
admits a smooth structure; if  is even, then
is even, then  admits a smooth structure if and only if the Kirby-Siebenmann invariant of
admits a smooth structure if and only if the Kirby-Siebenmann invariant of  is
is  .
.
-
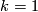 ,
,  is a simply-connected 5-manifold. The identification of
is a simply-connected 5-manifold. The identification of  with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
-
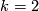 , we have a class of orientable 5-manifolds with fundamental group
, we have a class of orientable 5-manifolds with fundamental group  ,
, 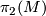 a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
[edit] 2.2 Connected sum along $S^1$
In the Smale-Barden's list of simply-connected 5-manifolds, manfolds are constructed from simple building blocks by the connected sum operation. In the world of manifolds with fundamental group  , the connected sum operation is not closed. The ``connected sum along
, the connected sum operation is not closed. The ``connected sum along  " operation
" operation 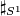 will do the job.
will do the job.
Definition 2.2.
Let 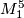 ,
, 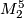 be two oriented 5-manifolds with
be two oriented 5-manifolds with 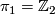 . Let
. Let 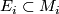 be the normal bundle of an embedded
be the normal bundle of an embedded  in
in 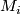 representing the nontrivial element in the fundamental group.
representing the nontrivial element in the fundamental group. 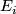 is a rank 4 trivial vector bundle over
is a rank 4 trivial vector bundle over  . Choose trivialisations of
. Choose trivialisations of 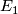 and
and 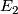 , and identify the disk bundles of
, and identify the disk bundles of 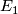 and
and 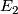 using the chosen identification (such that the identification is orientation-reversing, with respect to the induced orientations on the disk bundles from the ambient manifolds), we obtain a new manifold denoted by
using the chosen identification (such that the identification is orientation-reversing, with respect to the induced orientations on the disk bundles from the ambient manifolds), we obtain a new manifold denoted by 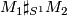 .
.
Notice that 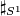 is not well-defined, the ambiguity comes from the identification of the two normal bundles, measured by
is not well-defined, the ambiguity comes from the identification of the two normal bundles, measured by 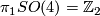 . To eliminate the ambiguity we need more structures on the tangent bundles of
. To eliminate the ambiguity we need more structures on the tangent bundles of 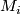 and require that
and require that 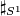 preserves the structures. (Analogous to the connected sum situation where orientations on manifolds are needed.) This will be explained in more detail in the next section.
preserves the structures. (Analogous to the connected sum situation where orientations on manifolds are needed.) This will be explained in more detail in the next section.
[edit] 3 Invariants
...
[edit] 4 Classification/Characterization
...
[edit] 5 Further discussion
...
[edit] 6 References
- [Barden] Template:Barden
- [Duan&Liang] Template:Duan&Liang
- [Hambleton&Su] Template:Hambleton&Su
- [Kervaire] Template:Kervaire
- [Markov] Template:Markov
- [Smale] Template:SmaleCatefory:5-Manifolds
From this point of view, the fist step one might take is the group  , which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group
, which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group  is the simplest one.)
is the simplest one.)
Any other point one should take into account concerning the classification of manifolds with nontrivial fundamental groups 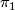 is that the higher homotopy groups
is that the higher homotopy groups 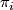 (
(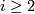 ) are modules over the group ring
) are modules over the group ring ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) , which are apparently homotopy invariants. Especially when we consider
, which are apparently homotopy invariants. Especially when we consider 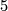 -manifolds
-manifolds 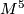 , the
, the ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) -module structure of
-module structure of 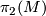 will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
Most part of this item will be a survey of the classification result of 5-manifolds 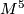 with fundamental group
with fundamental group 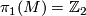 ,
, 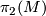 torsion free and is a trivial
torsion free and is a trivial ![\Zz[\Zz_2]](/images/math/0/6/e/06e45b437bee7ce0e2224a3e03e368b4.png) -module obtained in [Hambleton&Su] .
-module obtained in [Hambleton&Su] .
[edit] 2 Construction and examples
First some examples known from other context.
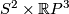 ;
;
-
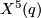
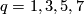 are the 5-dimensional fake real projective spaces with
are the 5-dimensional fake real projective spaces with 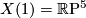 (There are exactly 4 in the smooth category). The meaning of
(There are exactly 4 in the smooth category). The meaning of  will be clear in the section ``Invariants".
will be clear in the section ``Invariants".
[edit] 2.1 Circle bundles over simply-connected 4-manifolds
Let 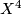 be a closed simply-connected topological 4-manifold,
be a closed simply-connected topological 4-manifold,  be a complex line bundle over
be a complex line bundle over  with Chern class
with Chern class 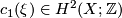 . Let the divisibility of
. Let the divisibility of 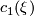 be
be  (i.e.
(i.e. 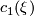 is
is  multiple of a primitive element in
multiple of a primitive element in 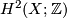 , then the sphere bundle
, then the sphere bundle 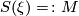 is a 5-manifold with fundament group
is a 5-manifold with fundament group 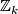 and
and 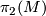 is a free abelian group of rank
is a free abelian group of rank 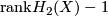 , and
, and 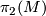 is a trivial module over the group ring. A priori
is a trivial module over the group ring. A priori  is a topological manifold. The smoothing problem is addressed by the following
is a topological manifold. The smoothing problem is addressed by the following
Proposition 2.1.[Hambleton&Su, Proposition 4.2]
Assume  is nontrivial. If
is nontrivial. If  is odd, then
is odd, then  admits a smooth structure; if
admits a smooth structure; if  is even, then
is even, then  admits a smooth structure if and only if the Kirby-Siebenmann invariant of
admits a smooth structure if and only if the Kirby-Siebenmann invariant of  is
is  .
.
-
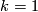 ,
,  is a simply-connected 5-manifold. The identification of
is a simply-connected 5-manifold. The identification of  with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
-
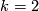 , we have a class of orientable 5-manifolds with fundamental group
, we have a class of orientable 5-manifolds with fundamental group  ,
, 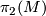 a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
[edit] 2.2 Connected sum along $S^1$
In the Smale-Barden's list of simply-connected 5-manifolds, manfolds are constructed from simple building blocks by the connected sum operation. In the world of manifolds with fundamental group  , the connected sum operation is not closed. The ``connected sum along
, the connected sum operation is not closed. The ``connected sum along  " operation
" operation 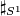 will do the job.
will do the job.
Definition 2.2.
Let 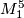 ,
, 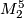 be two oriented 5-manifolds with
be two oriented 5-manifolds with 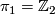 . Let
. Let 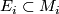 be the normal bundle of an embedded
be the normal bundle of an embedded  in
in 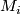 representing the nontrivial element in the fundamental group.
representing the nontrivial element in the fundamental group. 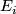 is a rank 4 trivial vector bundle over
is a rank 4 trivial vector bundle over  . Choose trivialisations of
. Choose trivialisations of 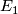 and
and 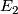 , and identify the disk bundles of
, and identify the disk bundles of 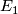 and
and 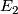 using the chosen identification (such that the identification is orientation-reversing, with respect to the induced orientations on the disk bundles from the ambient manifolds), we obtain a new manifold denoted by
using the chosen identification (such that the identification is orientation-reversing, with respect to the induced orientations on the disk bundles from the ambient manifolds), we obtain a new manifold denoted by 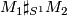 .
.
Notice that 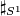 is not well-defined, the ambiguity comes from the identification of the two normal bundles, measured by
is not well-defined, the ambiguity comes from the identification of the two normal bundles, measured by 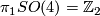 . To eliminate the ambiguity we need more structures on the tangent bundles of
. To eliminate the ambiguity we need more structures on the tangent bundles of 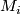 and require that
and require that 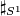 preserves the structures. (Analogous to the connected sum situation where orientations on manifolds are needed.) This will be explained in more detail in the next section.
preserves the structures. (Analogous to the connected sum situation where orientations on manifolds are needed.) This will be explained in more detail in the next section.
[edit] 3 Invariants
...
[edit] 4 Classification/Characterization
...
[edit] 5 Further discussion
...