3-manifolds in 6-space
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
Contents |
1 Introduction
Most of this page is intended not only for specialists in embeddings, but also for mathematicians from other areas who want to apply or to learn the theory of embeddings.
Basic results on embeddings of closed connected 3-manifolds in 6-space are particular cases of results on
embeddings of  -manifolds in
-manifolds in  -space, which are discussed in [Skopenkov2016e], [Skopenkov2006,
-space, which are discussed in [Skopenkov2016e], [Skopenkov2006,  2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case
2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case  .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum
3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum  of embeddings of closed connected 3-manifolds
of embeddings of closed connected 3-manifolds  in 6-space, and for the corresponding action of the group
in 6-space, and for the corresponding action of the group 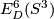 on the set
on the set 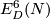 ,
see e.g. [Skopenkov2016c,
,
see e.g. [Skopenkov2016c,  4].
4].
2 Examples
For any integer  there is an embedding called the Hudson torus,
there is an embedding called the Hudson torus, 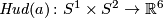 , see [Skopenkov2016e,
, see [Skopenkov2016e,  3], [Skopenkov2006, Example 2.10].
3], [Skopenkov2006, Example 2.10].
Piecewise smooth (PS) embedding and isotopy are defined in [Skopenkov2016f, Remark 1.1].
Example 2.1 (The Haefliger trefoil knot). There is a smooth embedding 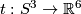 which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
This embedding represents a generator of 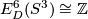 [Haefliger1966, Theorem 5.16].
[Haefliger1966, Theorem 5.16].
Let us construct the Haefliger (higher-dimensional) trefoil knot  [Haefliger1962,
[Haefliger1962,  4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in
4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in 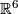 defined as follows. For coordinates in
defined as follows. For coordinates in  defined by
defined by 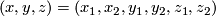 ,
the three 3-spheres are given by the following three systems of equations:
,
the three 3-spheres are given by the following three systems of equations:
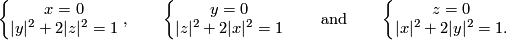
Take any orientations the 3-spheres [Haefliger1962,  4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate
4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate 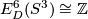 for any such choice). These orientations define an embedding
for any such choice). These orientations define an embedding 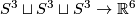 up to isotopy. The Haefliger trefoil
up to isotopy. The Haefliger trefoil  is the embedded connected sum of the components of this embedding.
is the embedded connected sum of the components of this embedding.
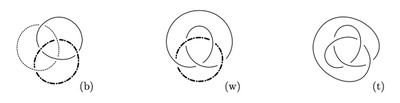
The construction of the Haefliger trefoil  is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link
is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link  . The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
. The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
For higher-dimensional generalizations see [Skopenkov2016h,  5] and [Skopenkov2016k].
5] and [Skopenkov2016k].
Example 2.2 (The Hopf embedding of  into
into 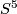 ).
Represent
).
Represent 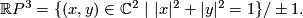 Define
Define
![\displaystyle h:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad h[(x,y)]=(x^2,\sqrt2xy,y^2).](/images/math/a/8/a/a8a67c9a1d736e528f511ad4ed420700.png)
It is easy to check that  is an embedding. (The image of this embedding in
is an embedding. (The image of this embedding in 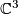 is given by the equations
is given by the equations  ,
, 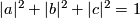 .)
.)
It would be interesting to obtain an explicit construction of an embedding 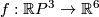 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion  . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
Example 2.3 (Algebraic embeddings from the theory of integrable systems).
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into  (given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
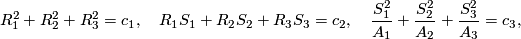
where 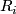 and
and 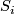 are real variables while
are real variables while 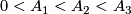 and
and 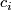 are constants.
For various choices of
are constants.
For various choices of 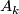 and
and 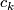 this system of equations defines embeddings of either
this system of equations defines embeddings of either  ,
, 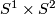 or
or 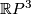 into
into  [Bolsinov&Fomenko2004, Chapter 14].
[Bolsinov&Fomenko2004, Chapter 14].
3 Classification
Recall that any 3-manifold embeds into  by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
Theorem 3.1 [Haefliger1966, Theorem 5.16].
There is an isomorphism 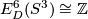 .
.
The following results of this subsection are proved in [Skopenkov2008] unless other references are given.
Let  be a closed connected oriented 3-manifold.
be a closed connected oriented 3-manifold.
For the next theorem, the Whitney invariant
 and and the Kreck invariant
and and the Kreck invariant 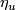 are defined in [Skopenkov2016e,
are defined in [Skopenkov2016e,  5] and in
5] and in  4 below.
For an abelian group
4 below.
For an abelian group  the divisibility of the zero element is zero, and the divisibility of
the divisibility of the zero element is zero, and the divisibility of 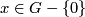 is
is 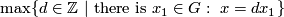 .
.
Theorem 3.2. (a) The Whitney invariant
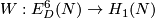
is surjective.
(b) For any 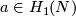 the Kreck invariant
the Kreck invariant
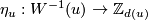
is bijective, where 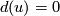 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of  .
.
Although part (a) first appeared in [Skopenkov2008], it is (as opposed to (b)) a simple corollary of results by Hudson and Haefliger.
All isotopy classes of embeddings 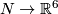 can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings
can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings 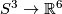 [Skopenkov2016c,
[Skopenkov2016c,  4], [Skopenkov2016e, Example 3.1].
4], [Skopenkov2016e, Example 3.1].
See a higher-dimensional generalization [Skopenkov2016e, Theorem 6.3].
Corollary 3.3. (a) If 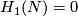 (i.e.
(i.e.  is an integral homology sphere), then the Kreck invariant
is an integral homology sphere), then the Kreck invariant 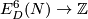 is a 1-1 correspondence.
is a 1-1 correspondence.
(b) If 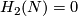 (i.e.
(i.e.  is a rational homology sphere, e.g.
is a rational homology sphere, e.g. 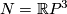 ), then
), then 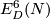 is in (non-canonical) 1-1 correspondence with
is in (non-canonical) 1-1 correspondence with 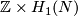 .
More precisely, the Whitney invariant
.
More precisely, the Whitney invariant 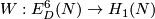 is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with
is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with  .
.
(c) Isotopy classes of embeddings 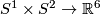 with zero Whitney invariant are in 1-1 correspondence with
with zero Whitney invariant are in 1-1 correspondence with  , and for any integer
, and for any integer 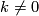 there are exactly
there are exactly 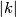 isotopy classes of embeddings
isotopy classes of embeddings 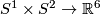 with the Whitney invariant
with the Whitney invariant  , cf. Corollary 3.5 below.
, cf. Corollary 3.5 below.
Part (a) was announced with a short outline of proof in [Hausmann1972], and proved in [Takase2006, Proof of Theorem 4.2 in p. 9 of the arxiv version]. For an alternative proof see [Skopenkov2008, Corollary (1) in p. 2 of the arxiv version].
Addendum 3.4.
If 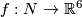 and
and 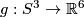 are embeddings, then
are embeddings, then
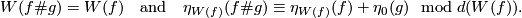
E. g. for 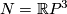 the embedded connected sum action of
the embedded connected sum action of 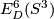 on
on 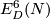 is free while for
is free while for 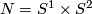 we have part (a) of the following corollary.
we have part (a) of the following corollary.
Corollary 3.5.
(a) There is an embedding 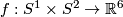 such that for any knot
such that for any knot 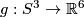 the embedding
the embedding 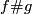 is isotopic to
is isotopic to  .
(We can take as
.
(We can take as  the Hudson torus
the Hudson torus 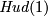 .)
.)
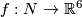 such that
such that 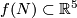 (e.g. for the standard embedding
(e.g. for the standard embedding Tex syntax error) and any non-trivial knot
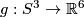 the embedding
the embedding 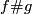 is not isotopic to
is not isotopic to  .
.
(We believe that this very corollary or the case 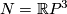 of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
For a related classification of some disconnected 3-manifolds in 6-space see [Skopenkov2016h,  6].
6].
4 The Kreck invariant
The Kreck invariant was invented by M. Kreck and appeared in [Skopenkov2008]. We work in the smooth category and use notation and conventions [Skopenkov2016c,  3]. Let
3]. Let  be a closed connected oriented 3-manifold and
be a closed connected oriented 3-manifold and 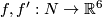 embeddings. Fix orientation on
embeddings. Fix orientation on  , and so on
, and so on 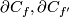 .
.
An orientation-preserving diffeomorphism 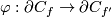 such that
such that 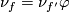 is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to
is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to  being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
Definition 4.1.
For a bundle isomorphism  denote
denote
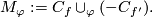
A bundle isomorphism 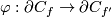 is called `spin', if
is called `spin', if 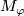 is spin.
is spin.
A spin bundle isomorphism exists [Skopenkov2008, Spin Lemma].
Indeed, the restrictions to  of
of  and
and  are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,
are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,  5], [Skopenkov2008,
5], [Skopenkov2008,  1, definition of the Whitney invariant]).
Define
1, definition of the Whitney invariant]).
Define  over
over  using an isotopy between the restrictions to
using an isotopy between the restrictions to  of
of  and
and  .
Since
.
Since 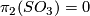 ,
,  extends to
extends to  .
Then
.
Then 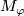 is spin.
is spin.
Identify with  the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product
the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product 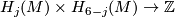 in homology of 6-manifolds
in homology of 6-manifolds  will be omitted.
will be omitted.
Definition 4.2.
Take a small oriented disk 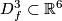 whose intersection with
whose intersection with  consists of exactly one point
of sign
consists of exactly one point
of sign 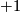 and such that
and such that 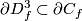 .
A `joint Seifert class' for
.
A `joint Seifert class' for 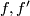 and a bundle isomorphism
and a bundle isomorphism 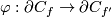 is a class
is a class
![\displaystyle Y\in H_4(M_\varphi)\quad\text{such that}\quad Y[\partial D^3_f]=1.](/images/math/3/d/c/3dc5178b68f6a78091cf6fc7750e7b87.png)
If 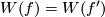 and
and  is a spin bundle isomorphism, then there is a joint Seifert class for
is a spin bundle isomorphism, then there is a joint Seifert class for
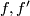 and
and  [Skopenkov2008, Agreement Lemma].
[Skopenkov2008, Agreement Lemma].
Denote by 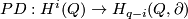 and
and 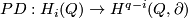 Poincaré duality (in any oriented manifold
Poincaré duality (in any oriented manifold 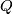 ).
).
Remark 4.3. The homology Alexander Duality isomorphism 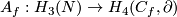 is defined in [Skopenkov2016f,
is defined in [Skopenkov2016f,  4].
4].
For 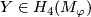 denote
denote ![Y\cap C_f:=PD[(PDY)|_{C_f}]\in H_4(C_f,\partial)](/images/math/7/3/8/73897b800b0d72e70bd87e27a2300686.png) .
If
.
If  is represented by a closed oriented 4-submanifold
is represented by a closed oriented 4-submanifold 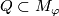 in general position to
in general position to 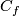 , then
, then 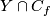 is represented by
is represented by 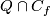 .
.
For a joint Seifert class 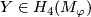 for
for  and
and  the classes
the classes
![\displaystyle Y\cap C_f=A_f[N]\quad\text{and}\quad Y\cap C_{f'}=A_{f'}[N]](/images/math/6/9/0/6905fa47d8fa67614555dbc17455f507.png)
are `homology Seifert surfaces' for  , cf. \cite[
, cf. \cite[  4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class
4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class  which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
Denote by 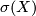 the signature of a 4-manifold
the signature of a 4-manifold  .
We use characteristic classes
.
We use characteristic classes 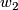 and
and 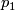 .
For a closed connected oriented 6-manifold
.
For a closed connected oriented 6-manifold 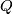 and
and 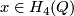 let the virtual signature of
let the virtual signature of 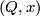 be
be
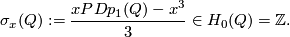
Since ![H_4(Q)\cong H^2(Q)\cong[Q,\Cc P^\infty]](/images/math/5/a/5/5a59c68771f06c0f517766cee026d75e.png) , there is a closed connected oriented 4-submanifold
, there is a closed connected oriented 4-submanifold 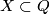 representing the class
representing the class  . Then
. Then 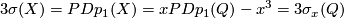 by [Hirzebruch1966, end of
by [Hirzebruch1966, end of  9.2] or else by [Skopenkov2008, Submanifold Lemma].
9.2] or else by [Skopenkov2008, Submanifold Lemma].
Definition 4.4. The `Kreck invariant' of two embeddings  and
and  such that
such that 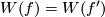 is defined by
is defined by
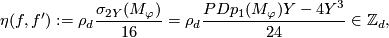
where 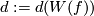 ,
, 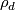 is the reduction modulo
is the reduction modulo  ,
, 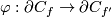 is a spin bundle isomorphism and
is a spin bundle isomorphism and 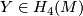 is a joint Seifert class for
is a joint Seifert class for 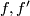 and
and  . Cf. [Ekholm2001, 4.1], [Zhubr2009].
. Cf. [Ekholm2001, 4.1], [Zhubr2009].
We have 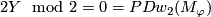 , so any closed connected oriented 4-submanifold of
, so any closed connected oriented 4-submanifold of 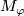 representing the class
representing the class 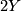 is spin, hence by the Rokhlin Theorem
is spin, hence by the Rokhlin Theorem 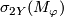 is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
For 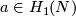 fix an embedding
fix an embedding 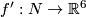 such that
such that 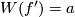 and define
and define 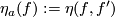 . (We write
. (We write 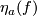 not
not 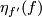 for simplicity.)
Then the map
for simplicity.)
Then the map 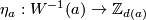 is well-defined by
is well-defined by ![\eta([f]):=\eta(f)](/images/math/9/7/8/9789b167fcce33386bc59efc9aaed109.png) .
.
The choice of the other orientation for  (resp.
(resp.  ) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection
) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection 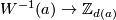 (resp. replaces it with the bijection
(resp. replaces it with the bijection 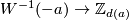 ).
).
Let us present a formula for the Kreck invariant analogous to [Guillou&Marin1986, Remarks to the four articles of Rokhlin, II.2.7 and III.excercises.IV.3], [Takase2004, Corollary 6.5], [Takase2006, Proposition 4.1]. This formula is useful when an embedding goes through  or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
The Kreck Invariant Lemma 4.5 [Skopenkov2008, The Kreck Invariant Lemma in p. 7 of the arxiv version]. Let
-
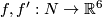 be two embeddings such that
be two embeddings such that 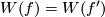 ,
,
-
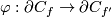 be a spin bundle isomorphism,
be a spin bundle isomorphism,
-
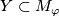 be a closed connected oriented 4-submanifold representing a joint Seifert class for
be a closed connected oriented 4-submanifold representing a joint Seifert class for 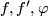 and
and
-
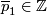 ,
, 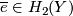 be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of
be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of  in
in 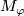 .
.
Then
![\displaystyle \frac{\sigma_{2[Y]}(M_\varphi)}{16}=\frac{\sigma(Y)-\overline p_1}8= \frac{\sigma(Y)-\overline e\cap\overline e}8.](/images/math/9/7/6/976d016617f48101c3311526cf28aa4a.png)
5 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Ekholm2001] T. Ekholm, Differential 3-knots in 5-space with and without self-intersections, Topology 40 (2001), no.1, 157–196. MR1791271 (2001h:57033) Zbl 0964.57029
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Haefliger1962] A. Haefliger, Knotted
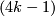 -spheres in
-spheres in 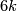 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hausmann1972] J. Hausmann, Plongements de sphères d'homologie, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A963–965. MR0315727 (47 #4276) Zbl 0244.57005
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Moriyama] T. Moriyama, Integral formula for an extension of Haefliger's embedding invariant, preprint.
- [Moriyama2008] T. Moriyama, An invariant of embeddings of 3-manifolds in 6-manifolds and Milnor's triple linking number, http://arxiv.org/abs/0806.3733
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Smale1959] S. Smale, Diffeomorphisms of the
 -sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
-sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Zhubr2009] A. V. Zhubr, Exotic invariant for 6-manifolds: a direct construction, Algebra i Analiz, 21:3 (2009), 145–164. English translation: St.Petersburg Math. J., 21:3 (2009).
 -space, which are discussed in [Skopenkov2016e], [Skopenkov2006,
-space, which are discussed in [Skopenkov2016e], [Skopenkov2006,  2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case
2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case  .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum
3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum  of embeddings of closed connected 3-manifolds
of embeddings of closed connected 3-manifolds  in 6-space, and for the corresponding action of the group
in 6-space, and for the corresponding action of the group 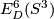 on the set
on the set 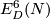 ,
see e.g. [Skopenkov2016c,
,
see e.g. [Skopenkov2016c,  4].
4].
2 Examples
For any integer  there is an embedding called the Hudson torus,
there is an embedding called the Hudson torus, 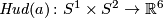 , see [Skopenkov2016e,
, see [Skopenkov2016e,  3], [Skopenkov2006, Example 2.10].
3], [Skopenkov2006, Example 2.10].
Piecewise smooth (PS) embedding and isotopy are defined in [Skopenkov2016f, Remark 1.1].
Example 2.1 (The Haefliger trefoil knot). There is a smooth embedding 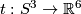 which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
This embedding represents a generator of 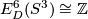 [Haefliger1966, Theorem 5.16].
[Haefliger1966, Theorem 5.16].
Let us construct the Haefliger (higher-dimensional) trefoil knot  [Haefliger1962,
[Haefliger1962,  4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in
4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in 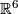 defined as follows. For coordinates in
defined as follows. For coordinates in  defined by
defined by 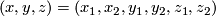 ,
the three 3-spheres are given by the following three systems of equations:
,
the three 3-spheres are given by the following three systems of equations:
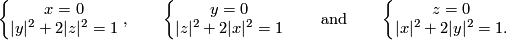
Take any orientations the 3-spheres [Haefliger1962,  4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate
4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate 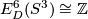 for any such choice). These orientations define an embedding
for any such choice). These orientations define an embedding 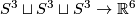 up to isotopy. The Haefliger trefoil
up to isotopy. The Haefliger trefoil  is the embedded connected sum of the components of this embedding.
is the embedded connected sum of the components of this embedding.
The construction of the Haefliger trefoil  is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link
is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link  . The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
. The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
For higher-dimensional generalizations see [Skopenkov2016h,  5] and [Skopenkov2016k].
5] and [Skopenkov2016k].
Example 2.2 (The Hopf embedding of 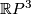 into
into 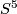 ).
Represent
).
Represent 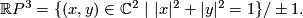 Define
Define
![\displaystyle h:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad h[(x,y)]=(x^2,\sqrt2xy,y^2).](/images/math/a/8/a/a8a67c9a1d736e528f511ad4ed420700.png)
It is easy to check that  is an embedding. (The image of this embedding in
is an embedding. (The image of this embedding in 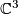 is given by the equations
is given by the equations 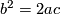 ,
, 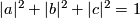 .)
.)
It would be interesting to obtain an explicit construction of an embedding 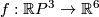 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion 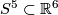 . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
Example 2.3 (Algebraic embeddings from the theory of integrable systems).
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into  (given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
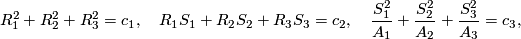
where  and
and 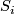 are real variables while
are real variables while 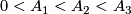 and
and 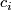 are constants.
For various choices of
are constants.
For various choices of 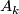 and
and 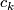 this system of equations defines embeddings of either
this system of equations defines embeddings of either  ,
, 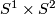 or
or 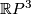 into
into  [Bolsinov&Fomenko2004, Chapter 14].
[Bolsinov&Fomenko2004, Chapter 14].
3 Classification
Recall that any 3-manifold embeds into  by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
Theorem 3.1 [Haefliger1966, Theorem 5.16].
There is an isomorphism 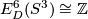 .
.
The following results of this subsection are proved in [Skopenkov2008] unless other references are given.
Let  be a closed connected oriented 3-manifold.
be a closed connected oriented 3-manifold.
For the next theorem, the Whitney invariant
 and and the Kreck invariant
and and the Kreck invariant 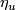 are defined in [Skopenkov2016e,
are defined in [Skopenkov2016e,  5] and in
5] and in  4 below.
For an abelian group
4 below.
For an abelian group  the divisibility of the zero element is zero, and the divisibility of
the divisibility of the zero element is zero, and the divisibility of 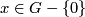 is
is 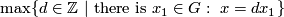 .
.
Theorem 3.2. (a) The Whitney invariant
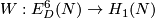
is surjective.
(b) For any 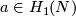 the Kreck invariant
the Kreck invariant
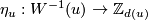
is bijective, where 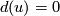 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of  .
.
Although part (a) first appeared in [Skopenkov2008], it is (as opposed to (b)) a simple corollary of results by Hudson and Haefliger.
All isotopy classes of embeddings 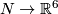 can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings
can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings 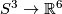 [Skopenkov2016c,
[Skopenkov2016c,  4], [Skopenkov2016e, Example 3.1].
4], [Skopenkov2016e, Example 3.1].
See a higher-dimensional generalization [Skopenkov2016e, Theorem 6.3].
Corollary 3.3. (a) If 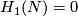 (i.e.
(i.e.  is an integral homology sphere), then the Kreck invariant
is an integral homology sphere), then the Kreck invariant 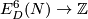 is a 1-1 correspondence.
is a 1-1 correspondence.
(b) If 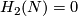 (i.e.
(i.e.  is a rational homology sphere, e.g.
is a rational homology sphere, e.g. 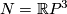 ), then
), then 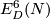 is in (non-canonical) 1-1 correspondence with
is in (non-canonical) 1-1 correspondence with 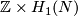 .
More precisely, the Whitney invariant
.
More precisely, the Whitney invariant 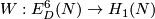 is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with
is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with  .
.
(c) Isotopy classes of embeddings 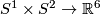 with zero Whitney invariant are in 1-1 correspondence with
with zero Whitney invariant are in 1-1 correspondence with  , and for any integer
, and for any integer 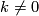 there are exactly
there are exactly 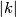 isotopy classes of embeddings
isotopy classes of embeddings 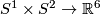 with the Whitney invariant
with the Whitney invariant  , cf. Corollary 3.5 below.
, cf. Corollary 3.5 below.
Part (a) was announced with a short outline of proof in [Hausmann1972], and proved in [Takase2006, Proof of Theorem 4.2 in p. 9 of the arxiv version]. For an alternative proof see [Skopenkov2008, Corollary (1) in p. 2 of the arxiv version].
Addendum 3.4.
If 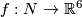 and
and 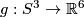 are embeddings, then
are embeddings, then
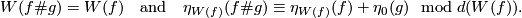
E. g. for 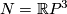 the embedded connected sum action of
the embedded connected sum action of 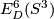 on
on 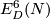 is free while for
is free while for 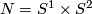 we have part (a) of the following corollary.
we have part (a) of the following corollary.
Corollary 3.5.
(a) There is an embedding 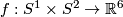 such that for any knot
such that for any knot 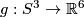 the embedding
the embedding 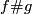 is isotopic to
is isotopic to  .
(We can take as
.
(We can take as  the Hudson torus
the Hudson torus 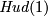 .)
.)
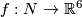 such that
such that 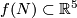 (e.g. for the standard embedding
(e.g. for the standard embedding Tex syntax error) and any non-trivial knot
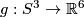 the embedding
the embedding 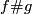 is not isotopic to
is not isotopic to  .
.
(We believe that this very corollary or the case 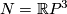 of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
For a related classification of some disconnected 3-manifolds in 6-space see [Skopenkov2016h,  6].
6].
4 The Kreck invariant
The Kreck invariant was invented by M. Kreck and appeared in [Skopenkov2008]. We work in the smooth category and use notation and conventions [Skopenkov2016c,  3]. Let
3]. Let  be a closed connected oriented 3-manifold and
be a closed connected oriented 3-manifold and 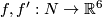 embeddings. Fix orientation on
embeddings. Fix orientation on  , and so on
, and so on 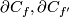 .
.
An orientation-preserving diffeomorphism 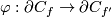 such that
such that 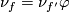 is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to
is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to  being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
Definition 4.1.
For a bundle isomorphism  denote
denote
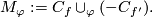
A bundle isomorphism 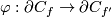 is called `spin', if
is called `spin', if 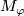 is spin.
is spin.
A spin bundle isomorphism exists [Skopenkov2008, Spin Lemma].
Indeed, the restrictions to  of
of  and
and  are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,
are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,  5], [Skopenkov2008,
5], [Skopenkov2008,  1, definition of the Whitney invariant]).
Define
1, definition of the Whitney invariant]).
Define  over
over  using an isotopy between the restrictions to
using an isotopy between the restrictions to  of
of  and
and  .
Since
.
Since  ,
,  extends to
extends to  .
Then
.
Then 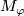 is spin.
is spin.
Identify with  the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product
the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product 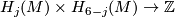 in homology of 6-manifolds
in homology of 6-manifolds  will be omitted.
will be omitted.
Definition 4.2.
Take a small oriented disk 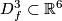 whose intersection with
whose intersection with  consists of exactly one point
of sign
consists of exactly one point
of sign  and such that
and such that 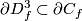 .
A `joint Seifert class' for
.
A `joint Seifert class' for 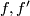 and a bundle isomorphism
and a bundle isomorphism 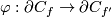 is a class
is a class
![\displaystyle Y\in H_4(M_\varphi)\quad\text{such that}\quad Y[\partial D^3_f]=1.](/images/math/3/d/c/3dc5178b68f6a78091cf6fc7750e7b87.png)
If 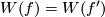 and
and  is a spin bundle isomorphism, then there is a joint Seifert class for
is a spin bundle isomorphism, then there is a joint Seifert class for
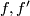 and
and  [Skopenkov2008, Agreement Lemma].
[Skopenkov2008, Agreement Lemma].
Denote by 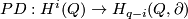 and
and 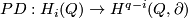 Poincaré duality (in any oriented manifold
Poincaré duality (in any oriented manifold 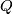 ).
).
Remark 4.3. The homology Alexander Duality isomorphism 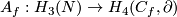 is defined in [Skopenkov2016f,
is defined in [Skopenkov2016f,  4].
4].
For 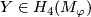 denote
denote ![Y\cap C_f:=PD[(PDY)|_{C_f}]\in H_4(C_f,\partial)](/images/math/7/3/8/73897b800b0d72e70bd87e27a2300686.png) .
If
.
If  is represented by a closed oriented 4-submanifold
is represented by a closed oriented 4-submanifold 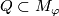 in general position to
in general position to 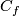 , then
, then 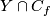 is represented by
is represented by 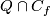 .
.
For a joint Seifert class 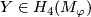 for
for  and
and  the classes
the classes
![\displaystyle Y\cap C_f=A_f[N]\quad\text{and}\quad Y\cap C_{f'}=A_{f'}[N]](/images/math/6/9/0/6905fa47d8fa67614555dbc17455f507.png)
are `homology Seifert surfaces' for  , cf. \cite[
, cf. \cite[  4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class
4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class  which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
Denote by 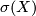 the signature of a 4-manifold
the signature of a 4-manifold  .
We use characteristic classes
.
We use characteristic classes 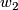 and
and 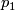 .
For a closed connected oriented 6-manifold
.
For a closed connected oriented 6-manifold 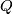 and
and 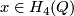 let the virtual signature of
let the virtual signature of 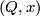 be
be
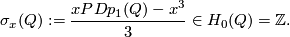
Since ![H_4(Q)\cong H^2(Q)\cong[Q,\Cc P^\infty]](/images/math/5/a/5/5a59c68771f06c0f517766cee026d75e.png) , there is a closed connected oriented 4-submanifold
, there is a closed connected oriented 4-submanifold 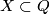 representing the class
representing the class  . Then
. Then 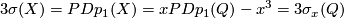 by [Hirzebruch1966, end of
by [Hirzebruch1966, end of  9.2] or else by [Skopenkov2008, Submanifold Lemma].
9.2] or else by [Skopenkov2008, Submanifold Lemma].
Definition 4.4. The `Kreck invariant' of two embeddings  and
and  such that
such that 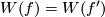 is defined by
is defined by
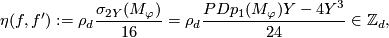
where 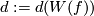 ,
,  is the reduction modulo
is the reduction modulo  ,
, 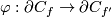 is a spin bundle isomorphism and
is a spin bundle isomorphism and 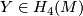 is a joint Seifert class for
is a joint Seifert class for 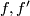 and
and  . Cf. [Ekholm2001, 4.1], [Zhubr2009].
. Cf. [Ekholm2001, 4.1], [Zhubr2009].
We have 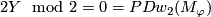 , so any closed connected oriented 4-submanifold of
, so any closed connected oriented 4-submanifold of 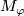 representing the class
representing the class 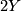 is spin, hence by the Rokhlin Theorem
is spin, hence by the Rokhlin Theorem 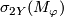 is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
For 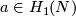 fix an embedding
fix an embedding 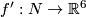 such that
such that 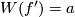 and define
and define 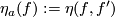 . (We write
. (We write 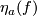 not
not 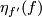 for simplicity.)
Then the map
for simplicity.)
Then the map 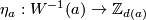 is well-defined by
is well-defined by ![\eta([f]):=\eta(f)](/images/math/9/7/8/9789b167fcce33386bc59efc9aaed109.png) .
.
The choice of the other orientation for  (resp.
(resp.  ) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection
) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection 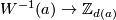 (resp. replaces it with the bijection
(resp. replaces it with the bijection 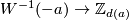 ).
).
Let us present a formula for the Kreck invariant analogous to [Guillou&Marin1986, Remarks to the four articles of Rokhlin, II.2.7 and III.excercises.IV.3], [Takase2004, Corollary 6.5], [Takase2006, Proposition 4.1]. This formula is useful when an embedding goes through 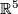 or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
The Kreck Invariant Lemma 4.5 [Skopenkov2008, The Kreck Invariant Lemma in p. 7 of the arxiv version]. Let
-
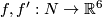 be two embeddings such that
be two embeddings such that 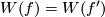 ,
,
-
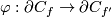 be a spin bundle isomorphism,
be a spin bundle isomorphism,
-
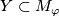 be a closed connected oriented 4-submanifold representing a joint Seifert class for
be a closed connected oriented 4-submanifold representing a joint Seifert class for 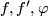 and
and
-
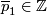 ,
, 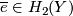 be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of
be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of  in
in 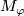 .
.
Then
![\displaystyle \frac{\sigma_{2[Y]}(M_\varphi)}{16}=\frac{\sigma(Y)-\overline p_1}8= \frac{\sigma(Y)-\overline e\cap\overline e}8.](/images/math/9/7/6/976d016617f48101c3311526cf28aa4a.png)
5 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Ekholm2001] T. Ekholm, Differential 3-knots in 5-space with and without self-intersections, Topology 40 (2001), no.1, 157–196. MR1791271 (2001h:57033) Zbl 0964.57029
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Haefliger1962] A. Haefliger, Knotted
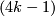 -spheres in
-spheres in 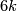 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hausmann1972] J. Hausmann, Plongements de sphères d'homologie, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A963–965. MR0315727 (47 #4276) Zbl 0244.57005
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Moriyama] T. Moriyama, Integral formula for an extension of Haefliger's embedding invariant, preprint.
- [Moriyama2008] T. Moriyama, An invariant of embeddings of 3-manifolds in 6-manifolds and Milnor's triple linking number, http://arxiv.org/abs/0806.3733
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Smale1959] S. Smale, Diffeomorphisms of the
 -sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
-sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Zhubr2009] A. V. Zhubr, Exotic invariant for 6-manifolds: a direct construction, Algebra i Analiz, 21:3 (2009), 145–164. English translation: St.Petersburg Math. J., 21:3 (2009).
 -space, which are discussed in [Skopenkov2016e], [Skopenkov2006,
-space, which are discussed in [Skopenkov2016e], [Skopenkov2006,  2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case
2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case  .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum
3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum  of embeddings of closed connected 3-manifolds
of embeddings of closed connected 3-manifolds  in 6-space, and for the corresponding action of the group
in 6-space, and for the corresponding action of the group 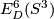 on the set
on the set 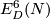 ,
see e.g. [Skopenkov2016c,
,
see e.g. [Skopenkov2016c,  4].
4].
2 Examples
For any integer  there is an embedding called the Hudson torus,
there is an embedding called the Hudson torus, 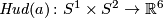 , see [Skopenkov2016e,
, see [Skopenkov2016e,  3], [Skopenkov2006, Example 2.10].
3], [Skopenkov2006, Example 2.10].
Piecewise smooth (PS) embedding and isotopy are defined in [Skopenkov2016f, Remark 1.1].
Example 2.1 (The Haefliger trefoil knot). There is a smooth embedding 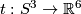 which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
This embedding represents a generator of 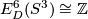 [Haefliger1966, Theorem 5.16].
[Haefliger1966, Theorem 5.16].
Let us construct the Haefliger (higher-dimensional) trefoil knot  [Haefliger1962,
[Haefliger1962,  4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in
4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in 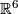 defined as follows. For coordinates in
defined as follows. For coordinates in  defined by
defined by 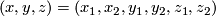 ,
the three 3-spheres are given by the following three systems of equations:
,
the three 3-spheres are given by the following three systems of equations:
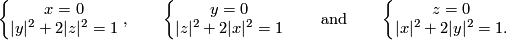
Take any orientations the 3-spheres [Haefliger1962,  4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate
4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate 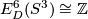 for any such choice). These orientations define an embedding
for any such choice). These orientations define an embedding 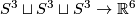 up to isotopy. The Haefliger trefoil
up to isotopy. The Haefliger trefoil  is the embedded connected sum of the components of this embedding.
is the embedded connected sum of the components of this embedding.
The construction of the Haefliger trefoil  is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link
is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link  . The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
. The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
For higher-dimensional generalizations see [Skopenkov2016h,  5] and [Skopenkov2016k].
5] and [Skopenkov2016k].
Example 2.2 (The Hopf embedding of 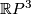 into
into 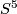 ).
Represent
).
Represent 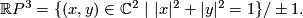 Define
Define
![\displaystyle h:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad h[(x,y)]=(x^2,\sqrt2xy,y^2).](/images/math/a/8/a/a8a67c9a1d736e528f511ad4ed420700.png)
It is easy to check that  is an embedding. (The image of this embedding in
is an embedding. (The image of this embedding in 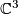 is given by the equations
is given by the equations 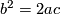 ,
, 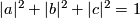 .)
.)
It would be interesting to obtain an explicit construction of an embedding 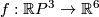 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion 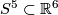 . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
Example 2.3 (Algebraic embeddings from the theory of integrable systems).
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into  (given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
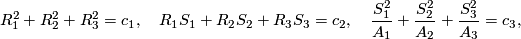
where  and
and  are real variables while
are real variables while 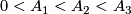 and
and 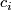 are constants.
For various choices of
are constants.
For various choices of 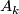 and
and 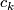 this system of equations defines embeddings of either
this system of equations defines embeddings of either  ,
, 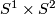 or
or 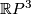 into
into  [Bolsinov&Fomenko2004, Chapter 14].
[Bolsinov&Fomenko2004, Chapter 14].
3 Classification
Recall that any 3-manifold embeds into  by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
Theorem 3.1 [Haefliger1966, Theorem 5.16].
There is an isomorphism 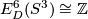 .
.
The following results of this subsection are proved in [Skopenkov2008] unless other references are given.
Let  be a closed connected oriented 3-manifold.
be a closed connected oriented 3-manifold.
For the next theorem, the Whitney invariant
 and and the Kreck invariant
and and the Kreck invariant 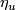 are defined in [Skopenkov2016e,
are defined in [Skopenkov2016e,  5] and in
5] and in  4 below.
For an abelian group
4 below.
For an abelian group  the divisibility of the zero element is zero, and the divisibility of
the divisibility of the zero element is zero, and the divisibility of 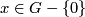 is
is 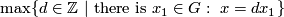 .
.
Theorem 3.2. (a) The Whitney invariant
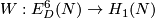
is surjective.
(b) For any 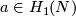 the Kreck invariant
the Kreck invariant
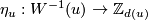
is bijective, where 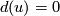 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of  .
.
Although part (a) first appeared in [Skopenkov2008], it is (as opposed to (b)) a simple corollary of results by Hudson and Haefliger.
All isotopy classes of embeddings 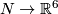 can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings
can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings 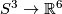 [Skopenkov2016c,
[Skopenkov2016c,  4], [Skopenkov2016e, Example 3.1].
4], [Skopenkov2016e, Example 3.1].
See a higher-dimensional generalization [Skopenkov2016e, Theorem 6.3].
Corollary 3.3. (a) If 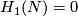 (i.e.
(i.e.  is an integral homology sphere), then the Kreck invariant
is an integral homology sphere), then the Kreck invariant 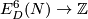 is a 1-1 correspondence.
is a 1-1 correspondence.
(b) If 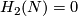 (i.e.
(i.e.  is a rational homology sphere, e.g.
is a rational homology sphere, e.g. 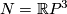 ), then
), then 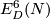 is in (non-canonical) 1-1 correspondence with
is in (non-canonical) 1-1 correspondence with 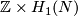 .
More precisely, the Whitney invariant
.
More precisely, the Whitney invariant 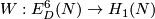 is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with
is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with  .
.
(c) Isotopy classes of embeddings  with zero Whitney invariant are in 1-1 correspondence with
with zero Whitney invariant are in 1-1 correspondence with  , and for any integer
, and for any integer 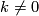 there are exactly
there are exactly 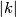 isotopy classes of embeddings
isotopy classes of embeddings 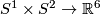 with the Whitney invariant
with the Whitney invariant  , cf. Corollary 3.5 below.
, cf. Corollary 3.5 below.
Part (a) was announced with a short outline of proof in [Hausmann1972], and proved in [Takase2006, Proof of Theorem 4.2 in p. 9 of the arxiv version]. For an alternative proof see [Skopenkov2008, Corollary (1) in p. 2 of the arxiv version].
Addendum 3.4.
If 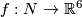 and
and 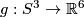 are embeddings, then
are embeddings, then
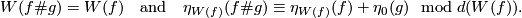
E. g. for 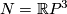 the embedded connected sum action of
the embedded connected sum action of  on
on 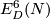 is free while for
is free while for 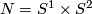 we have part (a) of the following corollary.
we have part (a) of the following corollary.
Corollary 3.5.
(a) There is an embedding 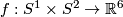 such that for any knot
such that for any knot 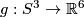 the embedding
the embedding 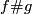 is isotopic to
is isotopic to  .
(We can take as
.
(We can take as  the Hudson torus
the Hudson torus 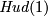 .)
.)
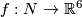 such that
such that 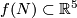 (e.g. for the standard embedding
(e.g. for the standard embedding Tex syntax error) and any non-trivial knot
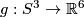 the embedding
the embedding 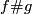 is not isotopic to
is not isotopic to  .
.
(We believe that this very corollary or the case 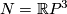 of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
For a related classification of some disconnected 3-manifolds in 6-space see [Skopenkov2016h,  6].
6].
4 The Kreck invariant
The Kreck invariant was invented by M. Kreck and appeared in [Skopenkov2008]. We work in the smooth category and use notation and conventions [Skopenkov2016c,  3]. Let
3]. Let  be a closed connected oriented 3-manifold and
be a closed connected oriented 3-manifold and 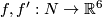 embeddings. Fix orientation on
embeddings. Fix orientation on  , and so on
, and so on 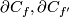 .
.
An orientation-preserving diffeomorphism 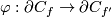 such that
such that 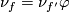 is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to
is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to  being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
Definition 4.1.
For a bundle isomorphism  denote
denote
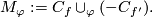
A bundle isomorphism 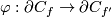 is called `spin', if
is called `spin', if 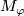 is spin.
is spin.
A spin bundle isomorphism exists [Skopenkov2008, Spin Lemma].
Indeed, the restrictions to  of
of  and
and  are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,
are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,  5], [Skopenkov2008,
5], [Skopenkov2008,  1, definition of the Whitney invariant]).
Define
1, definition of the Whitney invariant]).
Define  over
over  using an isotopy between the restrictions to
using an isotopy between the restrictions to  of
of  and
and  .
Since
.
Since  ,
,  extends to
extends to  .
Then
.
Then  is spin.
is spin.
Identify with  the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product
the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product 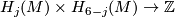 in homology of 6-manifolds
in homology of 6-manifolds  will be omitted.
will be omitted.
Definition 4.2.
Take a small oriented disk 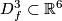 whose intersection with
whose intersection with  consists of exactly one point
of sign
consists of exactly one point
of sign 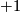 and such that
and such that 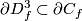 .
A `joint Seifert class' for
.
A `joint Seifert class' for 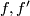 and a bundle isomorphism
and a bundle isomorphism 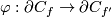 is a class
is a class
![\displaystyle Y\in H_4(M_\varphi)\quad\text{such that}\quad Y[\partial D^3_f]=1.](/images/math/3/d/c/3dc5178b68f6a78091cf6fc7750e7b87.png)
If 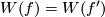 and
and  is a spin bundle isomorphism, then there is a joint Seifert class for
is a spin bundle isomorphism, then there is a joint Seifert class for
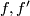 and
and  [Skopenkov2008, Agreement Lemma].
[Skopenkov2008, Agreement Lemma].
Denote by 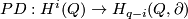 and
and 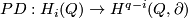 Poincaré duality (in any oriented manifold
Poincaré duality (in any oriented manifold 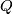 ).
).
Remark 4.3. The homology Alexander Duality isomorphism  is defined in [Skopenkov2016f,
is defined in [Skopenkov2016f,  4].
4].
For 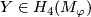 denote
denote ![Y\cap C_f:=PD[(PDY)|_{C_f}]\in H_4(C_f,\partial)](/images/math/7/3/8/73897b800b0d72e70bd87e27a2300686.png) .
If
.
If  is represented by a closed oriented 4-submanifold
is represented by a closed oriented 4-submanifold 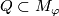 in general position to
in general position to 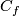 , then
, then 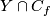 is represented by
is represented by 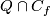 .
.
For a joint Seifert class 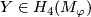 for
for  and
and  the classes
the classes
![\displaystyle Y\cap C_f=A_f[N]\quad\text{and}\quad Y\cap C_{f'}=A_{f'}[N]](/images/math/6/9/0/6905fa47d8fa67614555dbc17455f507.png)
are `homology Seifert surfaces' for  , cf. \cite[
, cf. \cite[  4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class
4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class  which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
Denote by 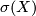 the signature of a 4-manifold
the signature of a 4-manifold  .
We use characteristic classes
.
We use characteristic classes 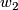 and
and 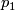 .
For a closed connected oriented 6-manifold
.
For a closed connected oriented 6-manifold 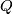 and
and 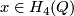 let the virtual signature of
let the virtual signature of 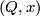 be
be
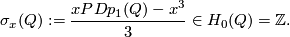
Since ![H_4(Q)\cong H^2(Q)\cong[Q,\Cc P^\infty]](/images/math/5/a/5/5a59c68771f06c0f517766cee026d75e.png) , there is a closed connected oriented 4-submanifold
, there is a closed connected oriented 4-submanifold 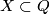 representing the class
representing the class  . Then
. Then 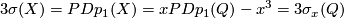 by [Hirzebruch1966, end of
by [Hirzebruch1966, end of  9.2] or else by [Skopenkov2008, Submanifold Lemma].
9.2] or else by [Skopenkov2008, Submanifold Lemma].
Definition 4.4. The `Kreck invariant' of two embeddings  and
and  such that
such that  is defined by
is defined by
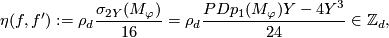
where 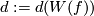 ,
,  is the reduction modulo
is the reduction modulo  ,
,  is a spin bundle isomorphism and
is a spin bundle isomorphism and 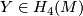 is a joint Seifert class for
is a joint Seifert class for  and
and  . Cf. [Ekholm2001, 4.1], [Zhubr2009].
. Cf. [Ekholm2001, 4.1], [Zhubr2009].
We have 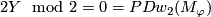 , so any closed connected oriented 4-submanifold of
, so any closed connected oriented 4-submanifold of  representing the class
representing the class 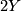 is spin, hence by the Rokhlin Theorem
is spin, hence by the Rokhlin Theorem 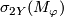 is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
For 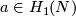 fix an embedding
fix an embedding 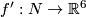 such that
such that 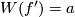 and define
and define 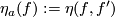 . (We write
. (We write 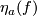 not
not 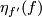 for simplicity.)
Then the map
for simplicity.)
Then the map 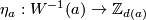 is well-defined by
is well-defined by ![\eta([f]):=\eta(f)](/images/math/9/7/8/9789b167fcce33386bc59efc9aaed109.png) .
.
The choice of the other orientation for  (resp.
(resp.  ) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection
) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection 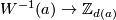 (resp. replaces it with the bijection
(resp. replaces it with the bijection 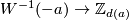 ).
).
Let us present a formula for the Kreck invariant analogous to [Guillou&Marin1986, Remarks to the four articles of Rokhlin, II.2.7 and III.excercises.IV.3], [Takase2004, Corollary 6.5], [Takase2006, Proposition 4.1]. This formula is useful when an embedding goes through 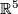 or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
The Kreck Invariant Lemma 4.5 [Skopenkov2008, The Kreck Invariant Lemma in p. 7 of the arxiv version]. Let
-
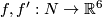 be two embeddings such that
be two embeddings such that 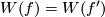 ,
,
-
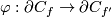 be a spin bundle isomorphism,
be a spin bundle isomorphism,
-
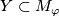 be a closed connected oriented 4-submanifold representing a joint Seifert class for
be a closed connected oriented 4-submanifold representing a joint Seifert class for 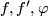 and
and
-
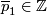 ,
, 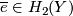 be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of
be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of  in
in 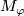 .
.
Then
![\displaystyle \frac{\sigma_{2[Y]}(M_\varphi)}{16}=\frac{\sigma(Y)-\overline p_1}8= \frac{\sigma(Y)-\overline e\cap\overline e}8.](/images/math/9/7/6/976d016617f48101c3311526cf28aa4a.png)
5 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Ekholm2001] T. Ekholm, Differential 3-knots in 5-space with and without self-intersections, Topology 40 (2001), no.1, 157–196. MR1791271 (2001h:57033) Zbl 0964.57029
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Haefliger1962] A. Haefliger, Knotted
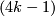 -spheres in
-spheres in 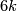 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hausmann1972] J. Hausmann, Plongements de sphères d'homologie, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A963–965. MR0315727 (47 #4276) Zbl 0244.57005
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Moriyama] T. Moriyama, Integral formula for an extension of Haefliger's embedding invariant, preprint.
- [Moriyama2008] T. Moriyama, An invariant of embeddings of 3-manifolds in 6-manifolds and Milnor's triple linking number, http://arxiv.org/abs/0806.3733
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Smale1959] S. Smale, Diffeomorphisms of the
 -sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
-sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Zhubr2009] A. V. Zhubr, Exotic invariant for 6-manifolds: a direct construction, Algebra i Analiz, 21:3 (2009), 145–164. English translation: St.Petersburg Math. J., 21:3 (2009).
 -space, which are discussed in [Skopenkov2016e], [Skopenkov2006,
-space, which are discussed in [Skopenkov2016e], [Skopenkov2006,  2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case
2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar to the case  .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum
3].
Unless specified otherwise, we work in the smooth category.
For definition of the
embedded connected sum  of embeddings of closed connected 3-manifolds
of embeddings of closed connected 3-manifolds  in 6-space, and for the corresponding action of the group
in 6-space, and for the corresponding action of the group 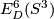 on the set
on the set 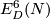 ,
see e.g. [Skopenkov2016c,
,
see e.g. [Skopenkov2016c,  4].
4].
2 Examples
For any integer  there is an embedding called the Hudson torus,
there is an embedding called the Hudson torus, 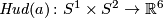 , see [Skopenkov2016e,
, see [Skopenkov2016e,  3], [Skopenkov2006, Example 2.10].
3], [Skopenkov2006, Example 2.10].
Piecewise smooth (PS) embedding and isotopy are defined in [Skopenkov2016f, Remark 1.1].
Example 2.1 (The Haefliger trefoil knot). There is a smooth embedding 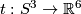 which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which is not smoothly isotopic to the standard embedding [Haefliger1962, Theorem 4.3], but is PS isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
This embedding represents a generator of 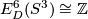 [Haefliger1966, Theorem 5.16].
[Haefliger1966, Theorem 5.16].
Let us construct the Haefliger (higher-dimensional) trefoil knot  [Haefliger1962,
[Haefliger1962,  4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in
4.1]. We start from the 3-dimensional Borromean rings (see Figure 6 of [Skopenkov2016h]), which are three disjoint 3-spheres in 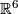 defined as follows. For coordinates in
defined as follows. For coordinates in  defined by
defined by 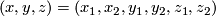 ,
the three 3-spheres are given by the following three systems of equations:
,
the three 3-spheres are given by the following three systems of equations:
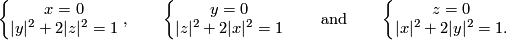
Take any orientations the 3-spheres [Haefliger1962,  4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate
4.1] (the isotopy class of the Haefliger trefoil knot could potentially depend on these orientations, but this isotopy class would generate  for any such choice). These orientations define an embedding
for any such choice). These orientations define an embedding  up to isotopy. The Haefliger trefoil
up to isotopy. The Haefliger trefoil  is the embedded connected sum of the components of this embedding.
is the embedded connected sum of the components of this embedding.
The construction of the Haefliger trefoil  is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link
is analogous to the construction of the trefoil from the 1-dimensional Borromean rings, depicted in Figure 1. An intermediate stage of the construction, when two components are connected but the third remains disjoint, yields the Whitehead link  . The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
. The 1-dimensional picture can also be regarded as a schematic picture for the construction of the Haefliger trefoil from the 3-dimensional Borromean rings.
For higher-dimensional generalizations see [Skopenkov2016h,  5] and [Skopenkov2016k].
5] and [Skopenkov2016k].
Example 2.2 (The Hopf embedding of 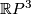 into
into 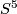 ).
Represent
).
Represent 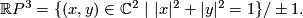 Define
Define
![\displaystyle h:\Rr P^3\to S^5\subset\Cc^3\quad\text{by}\quad h[(x,y)]=(x^2,\sqrt2xy,y^2).](/images/math/a/8/a/a8a67c9a1d736e528f511ad4ed420700.png)
It is easy to check that  is an embedding. (The image of this embedding in
is an embedding. (The image of this embedding in  is given by the equations
is given by the equations 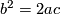 ,
, 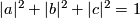 .)
.)
It would be interesting to obtain an explicit construction of an embedding 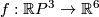 which is not isotopic to the composition of the Hopf embedding with the standard inclusion
which is not isotopic to the composition of the Hopf embedding with the standard inclusion 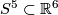 . (Such an embedding
. (Such an embedding  is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
is unique up to PL isotopy by the classical classification results just below the stable range, see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].)
Example 2.3 (Algebraic embeddings from the theory of integrable systems).
Some 3-manifolds appear in the theory of integrable systems together with their embeddings into  (given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
(given by a system of algebraic equations) [Bolsinov&Fomenko2004, Chapter 14]. E.g. the following system of equations corresponds to the Euler integrability case [Bolsinov&Fomenko2004, Chapter 14]:
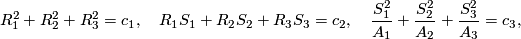
where 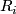 and
and 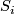 are real variables while
are real variables while 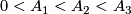 and
and 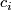 are constants.
For various choices of
are constants.
For various choices of 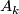 and
and 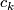 this system of equations defines embeddings of either
this system of equations defines embeddings of either  ,
, 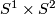 or
or 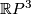 into
into  [Bolsinov&Fomenko2004, Chapter 14].
[Bolsinov&Fomenko2004, Chapter 14].
3 Classification
Recall that any 3-manifold embeds into  by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
by the strong Whitney embedding theorem [Skopenkov2006, Theorem 2.2.a].
For the classical classification
in the PL category see [Skopenkov2016e, Theorem 2.1], [Skopenkov2006, Theorem 2.13].
Theorem 3.1 [Haefliger1966, Theorem 5.16].
There is an isomorphism 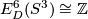 .
.
The following results of this subsection are proved in [Skopenkov2008] unless other references are given.
Let  be a closed connected oriented 3-manifold.
be a closed connected oriented 3-manifold.
For the next theorem, the Whitney invariant
 and and the Kreck invariant
and and the Kreck invariant 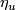 are defined in [Skopenkov2016e,
are defined in [Skopenkov2016e,  5] and in
5] and in  4 below.
For an abelian group
4 below.
For an abelian group  the divisibility of the zero element is zero, and the divisibility of
the divisibility of the zero element is zero, and the divisibility of  is
is 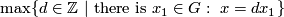 .
.
Theorem 3.2. (a) The Whitney invariant
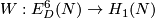
is surjective.
(b) For any 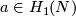 the Kreck invariant
the Kreck invariant
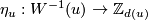
is bijective, where  is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of  .
.
Although part (a) first appeared in [Skopenkov2008], it is (as opposed to (b)) a simple corollary of results by Hudson and Haefliger.
All isotopy classes of embeddings  can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings
can be constructed from a certain given embedding using
unlinked and linked embedded connected sum with embeddings  [Skopenkov2016c,
[Skopenkov2016c,  4], [Skopenkov2016e, Example 3.1].
4], [Skopenkov2016e, Example 3.1].
See a higher-dimensional generalization [Skopenkov2016e, Theorem 6.3].
Corollary 3.3. (a) If 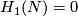 (i.e.
(i.e.  is an integral homology sphere), then the Kreck invariant
is an integral homology sphere), then the Kreck invariant 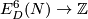 is a 1-1 correspondence.
is a 1-1 correspondence.
(b) If 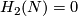 (i.e.
(i.e.  is a rational homology sphere, e.g.
is a rational homology sphere, e.g. 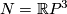 ), then
), then 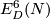 is in (non-canonical) 1-1 correspondence with
is in (non-canonical) 1-1 correspondence with 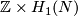 .
More precisely, the Whitney invariant
.
More precisely, the Whitney invariant 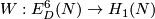 is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with
is surjective, and every its preimage is in
canonical 1-1 correspondence (given by the Kreck invariant) with  .
.
(c) Isotopy classes of embeddings 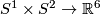 with zero Whitney invariant are in 1-1 correspondence with
with zero Whitney invariant are in 1-1 correspondence with  , and for any integer
, and for any integer  there are exactly
there are exactly 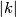 isotopy classes of embeddings
isotopy classes of embeddings 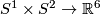 with the Whitney invariant
with the Whitney invariant  , cf. Corollary 3.5 below.
, cf. Corollary 3.5 below.
Part (a) was announced with a short outline of proof in [Hausmann1972], and proved in [Takase2006, Proof of Theorem 4.2 in p. 9 of the arxiv version]. For an alternative proof see [Skopenkov2008, Corollary (1) in p. 2 of the arxiv version].
Addendum 3.4.
If 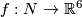 and
and 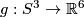 are embeddings, then
are embeddings, then
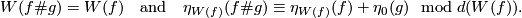
E. g. for 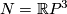 the embedded connected sum action of
the embedded connected sum action of  on
on  is free while for
is free while for 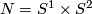 we have part (a) of the following corollary.
we have part (a) of the following corollary.
Corollary 3.5.
(a) There is an embedding 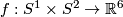 such that for any knot
such that for any knot 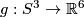 the embedding
the embedding 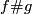 is isotopic to
is isotopic to  .
(We can take as
.
(We can take as  the Hudson torus
the Hudson torus 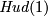 .)
.)
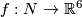 such that
such that 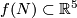 (e.g. for the standard embedding
(e.g. for the standard embedding Tex syntax error) and any non-trivial knot
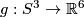 the embedding
the embedding 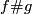 is not isotopic to
is not isotopic to  .
.
(We believe that this very corollary or the case 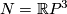 of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
of Theorem 3.2 are as hard to prove as the general case of Theorem 3.2.)
For a related classification of some disconnected 3-manifolds in 6-space see [Skopenkov2016h,  6].
6].
4 The Kreck invariant
The Kreck invariant was invented by M. Kreck and appeared in [Skopenkov2008]. We work in the smooth category and use notation and conventions [Skopenkov2016c,  3]. Let
3]. Let  be a closed connected oriented 3-manifold and
be a closed connected oriented 3-manifold and 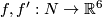 embeddings. Fix orientation on
embeddings. Fix orientation on  , and so on
, and so on 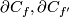 .
.
An orientation-preserving diffeomorphism 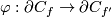 such that
such that 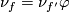 is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to
is called a bundle isomorphism. (By [Smale1959, Theorem A] this is equivalent to  being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
being isotopic to the restriction of a vector bundle isomorphism to the spherical bundle.)
Definition 4.1.
For a bundle isomorphism  denote
denote
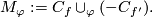
A bundle isomorphism 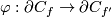 is called `spin', if
is called `spin', if 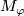 is spin.
is spin.
A spin bundle isomorphism exists [Skopenkov2008, Spin Lemma].
Indeed, the restrictions to  of
of  and
and  are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,
are isotopic (this is proved in definition of the Whitney invariant [Skopenkov2016e,  5], [Skopenkov2008,
5], [Skopenkov2008,  1, definition of the Whitney invariant]).
Define
1, definition of the Whitney invariant]).
Define  over
over  using an isotopy between the restrictions to
using an isotopy between the restrictions to  of
of  and
and  .
Since
.
Since 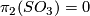 ,
,  extends to
extends to  .
Then
.
Then 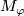 is spin.
is spin.
Identify with  the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product
the zero-dimensional homology group of a closed connected oriented manifold. The symbol of the intersection product 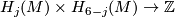 in homology of 6-manifolds
in homology of 6-manifolds  will be omitted.
will be omitted.
Definition 4.2.
Take a small oriented disk 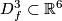 whose intersection with
whose intersection with  consists of exactly one point
of sign
consists of exactly one point
of sign  and such that
and such that  .
A `joint Seifert class' for
.
A `joint Seifert class' for  and a bundle isomorphism
and a bundle isomorphism 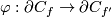 is a class
is a class
![\displaystyle Y\in H_4(M_\varphi)\quad\text{such that}\quad Y[\partial D^3_f]=1.](/images/math/3/d/c/3dc5178b68f6a78091cf6fc7750e7b87.png)
If 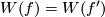 and
and  is a spin bundle isomorphism, then there is a joint Seifert class for
is a spin bundle isomorphism, then there is a joint Seifert class for
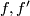 and
and  [Skopenkov2008, Agreement Lemma].
[Skopenkov2008, Agreement Lemma].
Denote by 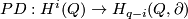 and
and 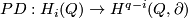 Poincaré duality (in any oriented manifold
Poincaré duality (in any oriented manifold 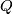 ).
).
Remark 4.3. The homology Alexander Duality isomorphism 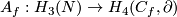 is defined in [Skopenkov2016f,
is defined in [Skopenkov2016f,  4].
4].
For 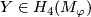 denote
denote ![Y\cap C_f:=PD[(PDY)|_{C_f}]\in H_4(C_f,\partial)](/images/math/7/3/8/73897b800b0d72e70bd87e27a2300686.png) .
If
.
If  is represented by a closed oriented 4-submanifold
is represented by a closed oriented 4-submanifold 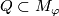 in general position to
in general position to 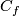 , then
, then 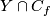 is represented by
is represented by 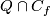 .
.
For a joint Seifert class 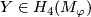 for
for  and
and  the classes
the classes
![\displaystyle Y\cap C_f=A_f[N]\quad\text{and}\quad Y\cap C_{f'}=A_{f'}[N]](/images/math/6/9/0/6905fa47d8fa67614555dbc17455f507.png)
are `homology Seifert surfaces' for  , cf. \cite[
, cf. \cite[  4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class
4 ]{Skopenkov2016f}.
This property provides an equivalent definition of a joint Seifert class  which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
which explains the name and which was used in [Skopenkov2008] together with the name `joint homology Seifert surface'.
Denote by 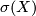 the signature of a 4-manifold
the signature of a 4-manifold  .
We use characteristic classes
.
We use characteristic classes  and
and  .
For a closed connected oriented 6-manifold
.
For a closed connected oriented 6-manifold 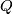 and
and 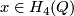 let the virtual signature of
let the virtual signature of 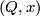 be
be
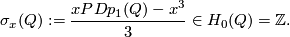
Since ![H_4(Q)\cong H^2(Q)\cong[Q,\Cc P^\infty]](/images/math/5/a/5/5a59c68771f06c0f517766cee026d75e.png) , there is a closed connected oriented 4-submanifold
, there is a closed connected oriented 4-submanifold 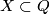 representing the class
representing the class  . Then
. Then 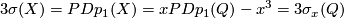 by [Hirzebruch1966, end of
by [Hirzebruch1966, end of  9.2] or else by [Skopenkov2008, Submanifold Lemma].
9.2] or else by [Skopenkov2008, Submanifold Lemma].
Definition 4.4. The `Kreck invariant' of two embeddings  and
and  such that
such that  is defined by
is defined by
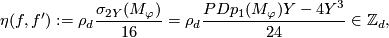
where 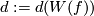 ,
, 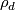 is the reduction modulo
is the reduction modulo  ,
, 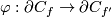 is a spin bundle isomorphism and
is a spin bundle isomorphism and 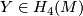 is a joint Seifert class for
is a joint Seifert class for 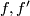 and
and  . Cf. [Ekholm2001, 4.1], [Zhubr2009].
. Cf. [Ekholm2001, 4.1], [Zhubr2009].
We have 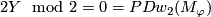 , so any closed connected oriented 4-submanifold of
, so any closed connected oriented 4-submanifold of 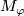 representing the class
representing the class  is spin, hence by the Rokhlin Theorem
is spin, hence by the Rokhlin Theorem 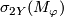 is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
is indeed divisible by 16. The Kreck invariant is well-defined by [Skopenkov2008, Independence Lemma].
For 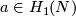 fix an embedding
fix an embedding 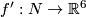 such that
such that 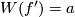 and define
and define 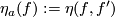 . (We write
. (We write 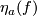 not
not 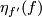 for simplicity.)
Then the map
for simplicity.)
Then the map  is well-defined by
is well-defined by ![\eta([f]):=\eta(f)](/images/math/9/7/8/9789b167fcce33386bc59efc9aaed109.png) .
.
The choice of the other orientation for  (resp.
(resp.  ) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection
) will in general give rise to different values for the Kreck invariant. But such a choice only permutes the bijection 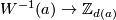 (resp. replaces it with the bijection
(resp. replaces it with the bijection 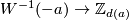 ).
).
Let us present a formula for the Kreck invariant analogous to [Guillou&Marin1986, Remarks to the four articles of Rokhlin, II.2.7 and III.excercises.IV.3], [Takase2004, Corollary 6.5], [Takase2006, Proposition 4.1]. This formula is useful when an embedding goes through  or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
or is given by a system of equations (because we can obtain a `Seifert surface' by changing the equality to the inequality in one
of the equations). See also [Moriyama], [Moriyama2008].
The Kreck Invariant Lemma 4.5 [Skopenkov2008, The Kreck Invariant Lemma in p. 7 of the arxiv version]. Let
-
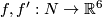 be two embeddings such that
be two embeddings such that 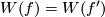 ,
,
-
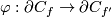 be a spin bundle isomorphism,
be a spin bundle isomorphism,
-
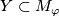 be a closed connected oriented 4-submanifold representing a joint Seifert class for
be a closed connected oriented 4-submanifold representing a joint Seifert class for  and
and
-
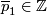 ,
, 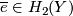 be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of
be the Pontryagin number and Poincaré dual of the Euler classes of the normal bundle of  in
in 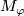 .
.
Then
![\displaystyle \frac{\sigma_{2[Y]}(M_\varphi)}{16}=\frac{\sigma(Y)-\overline p_1}8= \frac{\sigma(Y)-\overline e\cap\overline e}8.](/images/math/9/7/6/976d016617f48101c3311526cf28aa4a.png)
5 References
- [Bolsinov&Fomenko2004] A. V. Bolsinov and A. T. Fomenko, Integrable Hamiltonian systems, Chapman \& Hall/CRC, Boca Raton, FL, 2004. MR2036760 (2004j:37106) Zbl 1056.37075
- [Ekholm2001] T. Ekholm, Differential 3-knots in 5-space with and without self-intersections, Topology 40 (2001), no.1, 157–196. MR1791271 (2001h:57033) Zbl 0964.57029
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Haefliger1962] A. Haefliger, Knotted
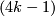 -spheres in
-spheres in 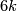 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hausmann1972] J. Hausmann, Plongements de sphères d'homologie, C. R. Acad. Sci. Paris Sér. A-B 275 (1972), A963–965. MR0315727 (47 #4276) Zbl 0244.57005
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Moriyama] T. Moriyama, Integral formula for an extension of Haefliger's embedding invariant, preprint.
- [Moriyama2008] T. Moriyama, An invariant of embeddings of 3-manifolds in 6-manifolds and Milnor's triple linking number, http://arxiv.org/abs/0806.3733
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Smale1959] S. Smale, Diffeomorphisms of the
 -sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
-sphere, Proc. Amer. Math. Soc. 10 (1959), 621–626. MR0112149 (22 #3004) Zbl 0118.39103
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Zhubr2009] A. V. Zhubr, Exotic invariant for 6-manifolds: a direct construction, Algebra i Analiz, 21:3 (2009), 145–164. English translation: St.Petersburg Math. J., 21:3 (2009).