Π-trivial map
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
This page is based on [Ranicki2002]. A map 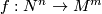 between manifolds represents a homology class
between manifolds represents a homology class ![f_*[N] \in H_n(M)](/images/math/3/d/2/3d21d4bf00b5770f8382bf0d70aa035e.png) . Let
. Let 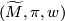 be an oriented cover with covering map
be an oriented cover with covering map 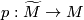 . If
. If  factors through
factors through 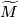 as
as 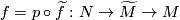 then
then  represents a homology class
represents a homology class ![\widetilde{f}_*[N]\in H_n(\widetilde{M})](/images/math/c/a/a/caa1901615f9a1811d1f344376d0e5a2.png) . Note that a choice of lift
. Note that a choice of lift 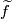 is required in order to represent a homology class.
is required in order to represent a homology class.
Let 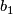 be a basepoint of
be a basepoint of  . By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map
. By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map 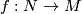 can be lifted to
can be lifted to 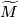 if and only if
if and only if 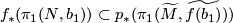 , i.e. if and only if the composition
, i.e. if and only if the composition 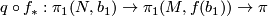 is trivial for
is trivial for 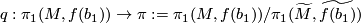 the quotient map.
the quotient map.
The group  is well-defined for any choice of lift
is well-defined for any choice of lift 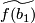 since
since 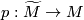 is a regular covering and changing the basepoint in
is a regular covering and changing the basepoint in 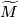 to a different lift corresponds to conjugating
to a different lift corresponds to conjugating 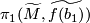 by some
by some 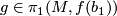 .
.
2 Definition
Let  be an
be an  -dimensional manifold and let
-dimensional manifold and let 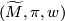 be an oriented cover. A
be an oriented cover. A  -trivial map
-trivial map 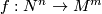 is a map from an oriented manifold
is a map from an oriented manifold  with basepoint
with basepoint 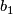 such that the composite
such that the composite
![\displaystyle \xymatrix{ \pi_1(N,b_1) \ar[r]^-{f_*} & \pi_1(M,f(b_1)) \ar[r] & \pi }](/images/math/c/e/3/ce3bcb9515d2da35fe37b876a521d6bb.png)
is trivial, together with a choice of lift 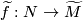 .
.
3 Properties
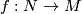 that factors through
that factors through 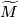 must map all of
must map all of  to the same sheet of
to the same sheet of 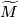 , hence the pullback satisfies
, hence the pullback satisfies 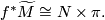
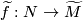 , which thought of as a map from
, which thought of as a map from 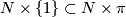 extends equivariantly to a lift
extends equivariantly to a lift 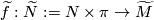 .
.
4 Lifts and paths - two alternative perspectives
Rather than taking a lift as part of the data for a  -trivial map we could instead take an equivalence class of paths in
-trivial map we could instead take an equivalence class of paths in  as is explained in this section. Since
as is explained in this section. Since  is the group of deck transformations of
is the group of deck transformations of 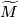 , the set of lifts
, the set of lifts 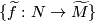 is non-canonically isomorphic to
is non-canonically isomorphic to  with the group structure determined by the action of
with the group structure determined by the action of  once a choice of lift
once a choice of lift 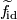 has been chosen to represent the identity element. In this way the choice of lift that is included as part of the data of a
has been chosen to represent the identity element. In this way the choice of lift that is included as part of the data of a  -trivial map can be thought of as a choice of isomorphism
-trivial map can be thought of as a choice of isomorphism
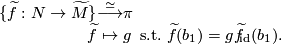
 be a basepoint of
be a basepoint of  . The set of homotopy classes of paths from
. The set of homotopy classes of paths from  to
to 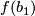 is non-canonically isomophic to
is non-canonically isomophic to 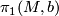 . An isomorphism is defined by a choice of path
. An isomorphism is defined by a choice of path ![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) to represent the identity element:
to represent the identity element: Tex syntax error
 denotes concatenation of paths and
denotes concatenation of paths and 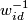 is the path
is the path 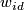 in reverse. Let
in reverse. Let 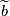 be a basepoint of
be a basepoint of 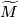 that is a lift of
that is a lift of  .
Define an equivalence relation
.
Define an equivalence relation 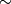 on this set by saying
on this set by saying ![\displaystyle [w]\sim[w^\prime] \iff [w^{-1}*w^\prime] \in p_*(\pi_1(\widetilde{M},\widetilde{b})).](/images/math/9/8/0/98019a1469641c8c2762306f91700b0c.png)
![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) descends to give an isomorphism
descends to give an isomorphism ![\displaystyle \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \;\longrightarrow\; \pi_1(M,b)/\pi_1(\widetilde{M},\widetilde{b})\cong \pi,](/images/math/2/6/0/26029500a0f65bc7905fbbbffaa82d91.png)
![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) to identify
to identify 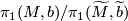 with
with 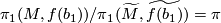 .
Thus a choice of lift
.
Thus a choice of lift 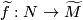 corresponds to a choice of homotopy class of paths from
corresponds to a choice of homotopy class of paths from  to
to 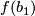 modulo
modulo 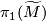 . A choice of lift
. A choice of lift 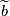 defines a bijection of sets
defines a bijection of sets ![\displaystyle \{\widetilde{f}:N\to \widetilde{M}\} \longleftrightarrow \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim](/images/math/3/b/9/3b91a8a4595ed359f53fa3eb5a0753e0.png)
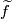 choose any path
choose any path 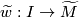 from
from 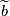 to
to 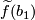 . Take the equivalence class of
. Take the equivalence class of 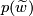 which is a path in
which is a path in  from
from  to
to 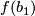 . Conversely given a choice of class
. Conversely given a choice of class ![\displaystyle [w]\in \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim](/images/math/c/9/e/c9ee0bc2859bb8ef4b1bb6508c79e344.png)
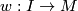 . This lifts uniquely to a path
. This lifts uniquely to a path 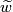 starting at
starting at 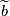 . Define a lift
. Define a lift 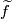 by setting
by setting 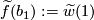 . Note this map is well-defined since different choices of representative
. Note this map is well-defined since different choices of representative  may differ by elements of
may differ by elements of 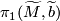 but their lifts will still end at the same point.
but their lifts will still end at the same point.
To sum up we have the following diagram of non-canonical isomorphisms and bijections
![\displaystyle \xymatrix{ \{\widetilde{f}:N\to \widetilde{M}\} \ar@{<->}[rr]^-{\widetilde{b}} \ar[dr]_-{\widetilde{f}_{id}} && \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \ar[dl]^-{[w_{id}]} \\ & \pi & }.](/images/math/d/3/d/d3d9b5d962bbd6495f83ad8b4d389724.png)
Since an oriented cover comes with a choice of lift 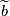 as part of the data a choice of identity lift corresponds to a choice of identity path, so it does not matter which we choose to include as part of the data for a
as part of the data a choice of identity lift corresponds to a choice of identity path, so it does not matter which we choose to include as part of the data for a  -trivial map.
-trivial map.
5 Examples
Let 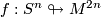 be an immersion and let
be an immersion and let 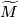 be the universal cover of
be the universal cover of  , let
, let 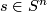 and
and 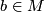 be basepoints. For
be basepoints. For  ,
, 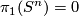 so
so  lifts to
lifts to 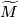 . An immersion
. An immersion 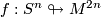 is a
is a 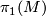 -trivial immersion as soon as a lift
-trivial immersion as soon as a lift 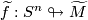 has been prescribed or, alternatively, once a homotopy class of paths
has been prescribed or, alternatively, once a homotopy class of paths 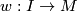 from
from  to
to 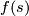 has been prescribed. A pair
has been prescribed. A pair 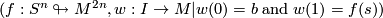 is often called a pointed immersion in the literature (See, for example, [Lück2001, Section 4.1]).
is often called a pointed immersion in the literature (See, for example, [Lück2001, Section 4.1]).
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001