Totally geodesic submanifold
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 11:57, 14 August 2013 and the changes since publication. |
|
The user responsible for this page is Hans-bert Rademacher. No other user may edit this page at present. |
Contents |
1 Definition
We consider a submanifold  of a Riemannian manifold
of a Riemannian manifold 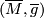 .
The Riemannian metric
.
The Riemannian metric 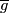 induces a Riemannian metric
induces a Riemannian metric  on the submanifold
on the submanifold
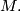 Then
Then 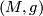 is also called a Riemannian submanifold of the Riemannian manifold
is also called a Riemannian submanifold of the Riemannian manifold 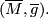
Definition 1.1.
A submanifold  of a Riemannian manifold
of a Riemannian manifold 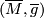 is called
totally geodesic if any geodesic on the submanifold
is called
totally geodesic if any geodesic on the submanifold  with its induced Riemannian metric
with its induced Riemannian metric  is also a geodesic on the Riemannian manifold
is also a geodesic on the Riemannian manifold 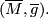
General references are [Chen2000, ch.11] and [Helgason1978, I §14].
On the Riemannian manifold 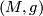 resp.
resp. 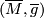 there exists an
unique torsion free and metric connection
there exists an
unique torsion free and metric connection  resp.
resp. 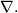 It is called the Levi-Civita connection.
Then the shape tensor or second fundamental form tensor
It is called the Levi-Civita connection.
Then the shape tensor or second fundamental form tensor 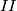 is a symmetric tensor field
which can be defined as follows
for tangent vectors
is a symmetric tensor field
which can be defined as follows
for tangent vectors 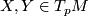 resp. vector fields
resp. vector fields 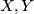 on the submanifold:
on the submanifold:
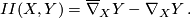
Proposition 1.2 (cf. [O'Neill1983, p.104]).
For a Riemannian submanifold 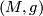 of the Riemannian manifold
of the Riemannian manifold
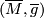 the following statements are equivalent:
the following statements are equivalent:
-
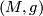 is a totally geodesic submanifold of
is a totally geodesic submanifold of 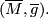
- The shape tensor vanishes:
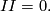
- For a vector
 tangential to the submanifold
tangential to the submanifold  the geodesic
the geodesic 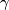 on the Riemannian manifold
on the Riemannian manifold 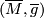 defined on a small interval
defined on a small interval 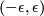 with initial direction
with initial direction 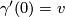 stays on the submanifold.
stays on the submanifold.
Part (c) implies that locally a totally geodesic submanifold 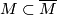 is uniquely determined
by the vector subspace
is uniquely determined
by the vector subspace 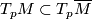 for some
for some 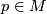 , provided that
, provided that  is connected and complete.
There is a result by É. Cartan providing necessary and sufficient conditions
for the existence of a totally geodesic submanifold
tangential to a given vector subspace
is connected and complete.
There is a result by É. Cartan providing necessary and sufficient conditions
for the existence of a totally geodesic submanifold
tangential to a given vector subspace  of the tangent space
of the tangent space 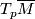 in terms of the curvature
tensor, cf. [Chen2000, 11.1]. This result shows that for most Riemannian manifolds
no totally geodesic submanifolds of dimension at least two exist.
On the other hand totally geodesic submanifolds do occur if the manifold
carries isometries:
in terms of the curvature
tensor, cf. [Chen2000, 11.1]. This result shows that for most Riemannian manifolds
no totally geodesic submanifolds of dimension at least two exist.
On the other hand totally geodesic submanifolds do occur if the manifold
carries isometries:
Theorem 1.3 (cf. [Klingenberg1995, 1.10.15]).
Let 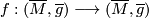 be an isometry of
the Riemannian manifold
be an isometry of
the Riemannian manifold 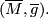 Then every connected component
Then every connected component
 of the
fixed point set
of the
fixed point set
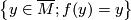
with the induced Riemannian metric is a totally geodesic submanifold.
2 Examples
Example 2.1.
- A geodesic
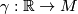 can be viewed as a totally geodesic submanifold of dimension one.
can be viewed as a totally geodesic submanifold of dimension one. - Consider the standard sphere For
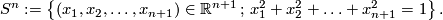
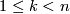 the
the  -sphere
-sphere
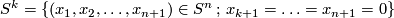
is a totally geodesic submanifold of
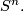 It is the fixed point set of the isometry
It is the fixed point set of the isometry 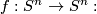 One can see immediately that any complete
One can see immediately that any complete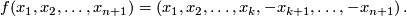
 -dimensional totally geodesic submanifold of
-dimensional totally geodesic submanifold of  is of this form up to an isometry of the sphere.
is of this form up to an isometry of the sphere. - We denote by
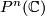 the
the  -dimensional complex projective space of one-dimensional linear subspaces of the complex vector space
-dimensional complex projective space of one-dimensional linear subspaces of the complex vector space 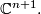 For
For 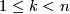 the inclusion
the inclusion 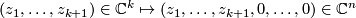 induces an inclusion of the
induces an inclusion of the  -dimensional complex projective space
-dimensional complex projective space 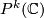 into
into 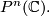 This is a totally geodesic submanifold since
it is the fixed point set of the isometry on
This is a totally geodesic submanifold since
it is the fixed point set of the isometry on 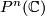 induced by
the reflection
induced by
the reflection 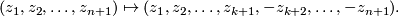
The last two examples are in particular examples of symmetric spaces. The totally geodesic submanifolds of a symmetric space can be described in terms of a Lie triple system, cf. [Helgason1978, ch.IV, §7] or [Chen2000, 11.2].
3 References
- [Chen2000] B. Chen, Riemannian submanifolds, in Hanbook of differential geometry, Vol. I, edited by F. J. E. Dillen and L. C. A. Verstraelen, North-Holland, 2000, 187–418. MR1736854 (2001b:53064) Zbl 1214.53014
- [Helgason1978] S. Helgason, Differential geometry, Lie groups, and symmetric spaces, Academic Press, Orlando, Dan Diego New York 1978. MR514561 (80k:53081) Zbl 0993.53002
- [Klingenberg1995] W. P. A. Klingenberg, Riemannian geometry, Walter de Gruyter & Co., 1995. MR1330918 (95m:53003) Zbl 1073.53006
- [O'Neill1983] B. O'Neill, Semi-Riemannian geometry, Academic Press Inc., 1983. MR719023 (85f:53002) Zbl 0531.53051
4 External links
- The Encylopedia of Mathematics article on Totally-geodesic_manifold
- The Wikipedia page about geodesics