Torsion in the B-bordism group for connective covers of BO
Contents |
[edit] 1 Question
For each connective cover of 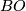 , i.e.
, i.e.  -connected space
-connected space 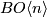 with a fibration
with a fibration 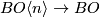 inducing an isomorphism on homotopy groups
inducing an isomorphism on homotopy groups 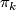 for
for 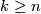 ,
there is a normal bordism group
,
there is a normal bordism group 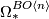 as defined in the article on B-bordism.
(The first examples are unoriented bordism, oriented bordism, spin bordism and string bordism.)
as defined in the article on B-bordism.
(The first examples are unoriented bordism, oriented bordism, spin bordism and string bordism.)
Question 1.1.
Which primes appear in the torsion part of 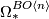 ?
?
[edit] 2 Answers
There is  -torsion in
-torsion in 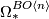 for all
for all  .
For
.
For  odd there is
odd there is  -torsion in
-torsion in 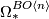 iff
iff 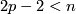 .
.
[edit] 3 Proof
Theorem 3.1 [Serre1951].
There is  -torsion in the framed bordism group (stable homotopy group of spheres)
-torsion in the framed bordism group (stable homotopy group of spheres)
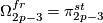 .
.
Corollary 3.2.
For 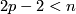 there is
there is  -torsion in
-torsion in 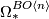 .
.
For the proof one shows that for 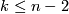 ,
,
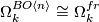 which follows from obstruction theory.
Thus there is
which follows from obstruction theory.
Thus there is  -torsion in
-torsion in 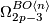 for
for 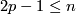 .
.
We denote by 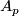 the mod
the mod  Steenrod algebra and by
Steenrod algebra and by 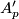 the subalgebra of the mod
the subalgebra of the mod  Steenrod algebra generated by reduced powers.
It is isomorphic to the quotient algebra
Steenrod algebra generated by reduced powers.
It is isomorphic to the quotient algebra 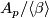 of the Steenrod algebra by the two-sided ideal
generated by the Bockstein operation.
of the Steenrod algebra by the two-sided ideal
generated by the Bockstein operation.
Theorem 3.3 [Milnor1960].
Let  be a connective spectrum with finitely many cells in each dimension.
If
be a connective spectrum with finitely many cells in each dimension.
If 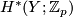 is a free
is a free 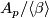 -module with even-dimensional generators,
then
-module with even-dimensional generators,
then 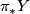 contains no
contains no  -torsion.
-torsion.
This is proved by finding a rather explicit free resolution
of 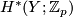 over the Steenrod algebra, and showing that the Adams
spectral sequence for
over the Steenrod algebra, and showing that the Adams
spectral sequence for ![[M(p),Y]](/images/math/e/c/7/ec72b7a283999f42bbbb1c2ecb3255ad.png) degenerates at the
degenerates at the 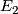 -term,
where
-term,
where 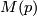 is the mod
is the mod  Moore spectrum.
Moore spectrum.
Theorem 3.4 [Giambalvo1969, Corollary 1].
For 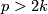 , the module
, the module 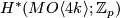 is a free module over
is a free module over 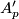 generated by the Thom class.
generated by the Thom class.
This uses the computation of 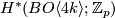 as a Hopf algebra,
the work by Milnor-Moore on Hopf algebras and the action of the Steenrod algebra on Pontryagin classes.
as a Hopf algebra,
the work by Milnor-Moore on Hopf algebras and the action of the Steenrod algebra on Pontryagin classes.
Corollary 3.5.
For 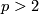 and
and 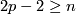 there is no
there is no  -torsion in
-torsion in 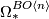 .
.
Here we use in addition to the two previous theorems that for 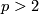 the
the  -torsion in
-torsion in 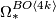 agrees with the
agrees with the  -torsion in
-torsion in 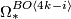 ,
, 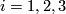 since the higher connective covers
are obtained by possibly taking homotopy fibers of maps to
since the higher connective covers
are obtained by possibly taking homotopy fibers of maps to 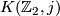 's.
's.
[edit] 4 Further discussion
It seems much harder to say more about the possible orders of torsion elements in 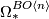 .
It is known that in unoriented, oriented and spin bordism each torsion element has order 2,
and that in string bordism the order of each torsion element divides 24.
.
It is known that in unoriented, oriented and spin bordism each torsion element has order 2,
and that in string bordism the order of each torsion element divides 24.
[edit] 5 References
- [Giambalvo1969] V. Giambalvo, The
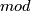
 cohomology of
cohomology of 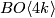 , Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
, Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
- [Milnor1960] J. Milnor, On the cobordism ring
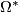 and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
- [Serre1951] J. Serre, Homologie singulière des espaces fibrès. Applications, Ann. of Math. (2) 54 (1951), 425–505. MR0045386 (13,574g) Zbl 0045.26003